Cel ćwiczenia

Celem ćwiczenia jest badanie zjawiska Dopplera dla fal dźwiękowych oraz wykorzystanie tego zjawiska do wyznaczania prędkości dźwięku w powietrzu.

Wstęp

Fale dźwiękowe

Na czym polega emisja dźwięku przez drgającą strunę? Drgania struny wprawiają w ruch drgający sąsiednie cząsteczki powietrza. One z kolei przekazują ruch drgający kolejnym cząsteczkom i w powietrzu rozchodzi się fala. Nazywamy tak zaburzenie rozprzestrzeniające się w ośrodku, gdy cząsteczki drgają wokół położeń równowagi, przekazując energię kolejnym cząsteczkom ośrodka, nie zmieniając przy tym swego średniego położenia. Fala dźwiękowa jest falą podłużną, czyli drgania cząsteczek ośrodka zachodzą w kierunku zgodnym z kierunkiem rozchodzenia się fali.

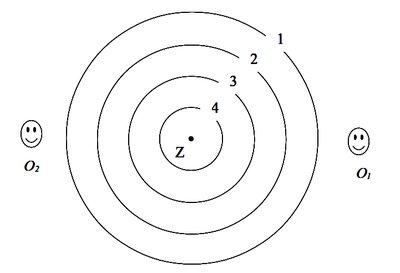Doppler rys1.pngRys.1. Fala dźwiękowa emitowana przez nieruchome źródło Z

Odległość między kolejnymi grzbietami nazywamy długością fali \(\lambda\). Taką odległość fala przebywa w czasie równym okresowi drgań cząsteczek ośrodka, czyli w czasie, w którym zachodzi jedno pełne drganie. Grzbiet fali oznaczony numerem 1 został wyemitowany jako pierwszy, po upływie jednego okresu został wyemitowany grzbiet oznaczony jako 2 itd.
Długość fali, to droga którą przebędzie fala w ciągu jednego okresu, równa jest iloczynowi prędkości rozchodzenia się fali \(v\) i okresu \(T\).
(1) $$\lambda=vT$$
Częstotliwością fali \(f\) nazywamy liczbę drgań zachodzących w jednostce czasu: 
(2) $$f = \frac{1}{T}$$
Możemy częstotliwość powiązać z długością fali wstawiając do wzoru (2) okres T wyznaczony z równania (1):
(3)$$f = \frac{v}{\lambda}$$
Częstotliwość i długość fali są więc wielkościami odwrotnie proporcjonalnymi. Dźwięki o dużej częstotliwości, a małej długości fali odbieramy jako dźwięki wysokie, a dźwięki o małej częstotliwości i dużej długości fali, to dla naszego ucha dźwięki niskie. W przypadku przedstawionym na Rys. 1. obaj obserwatorzy \(O_1\) i \(O_2\) odbierają falę dźwiękową o tej samej częstotliwości.
 
Efekt Dopplera
Jak zmieni się sytuacja przedstawiona na Rys. 1. gdy źródło dźwięku zacznie się poruszać? Załóżmy, że źródło  Z porusza się w prawo z prędkością \(v_z\). Pierwszy grzbiet fali wyemitowany został w chwili, gdy źródło było w położeniu \(Z_1,\) drugi – z położenia \(Z_2\) i tak dalej. W rezultacie obserwator \(O_1,\) do którego źródło dźwięku przybliża się, odbiera falę dźwiękową o wyższej częstotliwości niż od nieruchomego źródła dźwięku. W odwrotnej sytuacji jest obserwator  \(O_2,\) który odbiera falę dźwiękową z oddalającego się źródła. Do niego dochodzi dźwięk o niższej częstotliwości. 
Dobrze znamy to zjawisko z życia codziennego. Gdy stoimy przy ruchliwej szosie, nawet z zamkniętymi oczami potrafimy odgadnąć, kiedy mija nas samochód. W momencie mijania dźwięk jego silnika zmienia się z wyższego na niższy.
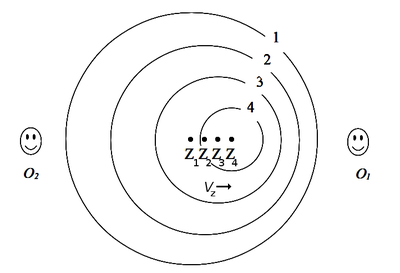Doppler rys2.pngRys. 2. Fala dźwiękowa emitowana przez źródło poruszające się z prędkością Vz

 

Poruszające się źródło dźwięku przebywa w czasie jednego okresu T drogę:
  (4) $$s = v_z T$$
O tyle mniejsza jest długość fali \(\lambda\) dochodzącej do obserwatora O1 od długości fali \(\lambda_z\) wysyłanej przez nieruchome źródło:
(5) $$\lambda = \lambda_z -s =\lambda_z- v_z T$$
Częstotliwość fali \(f\) odbieranej przez obserwatora \(O_1,\) zgodnie ze wzorem (3):
(6)$$f = \frac{v}{\lambda} = \frac{v}{\lambda_z- v_z T}$$
Gdzie \(v\) jest prędkością rozchodzenia się fali. Po prostych przekształceniach otrzymujemy:
(7)$$f = f_z \frac{v}{v-v_z}$$
\(T\) – okres fali generowanej przez źródło, 
\(f_Z\)– częstotliwość fali generowanej przez źródło,
\(f\) – częstotliwość fali odbieranej przez obserwatora,
\(\lambda_Z\) – długość fali generowanej przez źródło,
\(\lambda\) - długość fali odbieranej przez obserwatora,
\(v\) – prędkość rozchodzenia się fali
\(v_Z\) – prędkość źródła

 

Obliczenie częstotliwości fali dźwiękowej odbieranej przez obserwatora \(O_2\) jest przebiega podobnie, z tym, że długość fali dochodzącej do niego jest większa od długości fali \(\lambda_z\) wysyłanej przez nieruchome źródło: 
(8)$$\lambda = \lambda_z + s =\lambda_z + v_z T$$
Otrzymujemy więc częstotliwość fali dźwiękowej odbieranej przez obserwatora  \(O_2\):
(9) $$ f = f_z \frac{v}{v+v_z}$$
 

Opis układu pomiarowego

Źródło dźwięku znajduje się na wózeczku, który możemy wprawiać w ruch z zadaną prędkością. Dźwięk odbierany jest przez nieruchomy detektor, który mierzy częstotliwość dźwięku. Uklad do badania efektu Dopplera przedstawia fotografia na rys.3.

Uklad Doppler.pngRys.3. Układ do badania efektu Dopplera

Wykonanie ćwiczenia

Po zalogowaniu się do Laboratorium przyciskiem Podłącz wybieramy

Po naciśnięciu przycisku Start rozpoczyna się cykl pomiaru. Komputer sterujący ustawia początkową prędkość, którą po wykonaniu pomiaru, zmienia o wartość wynikającą z podziału różnicy prędkości końcowej i początkowej przez wybraną liczbę punktów pomiarowych. Poprzez sieć internetową wyniki pomiarów są sukcesywnie przesyłane na komputer użytkownika i wyświetlane na ekranie monitora w postaci wykresu zależności częstotliwości odebranej przez detektor od prędkościwózeczka. W dowolnej chwili można przerwać pomiar, zapisać dane na dysku, zmienić parametry i ponownie uruchomić pomiary.

Wykonujemy pomiar częstotliwości dźwięku dla nieruchomego źródła, a następnie dla źródła dźwięku poruszającego się. Wybieramy kilka (co najmniej 5) prędkości źródła dźwięku skierowanych w stronę detektora oraz kilka w kierunku przeciwnym'

Opracowanie wyników

W celu wyznaczenia prędkości dźwięku w powietrzu przekształcamy wzory (7) i (9):

(7a) $$v =\frac{f v_z}{f-f_z}$$     (źródło przybliża się) 

(9a) $$v =\frac{f v_z}{f_z-f}$$    (źródło oddala się) 
Można by użyć jednego ze wzorów (5a) i (7a) do wyznaczenia prędkości dźwięku w powietrzu. Użylibyśmy wtedy tylko jednego wyniku pomiaru częstotliwości poruszającego się źródła. Znacznie bardziej wiarygodny będzie wynik, gdy wykorzystamy wszystkie wykonane pomiary dla różnych prędkości źródła.

gdzie \(f_z\) to częstotliwość dźwięku nieruchomego źródła, \(f \) – częstotliwość dźwięku wysłanego przez źródło poruszające się z prędkością \(v_z\).

Zauważmy, że wzory (7a) i (9a) różnią się tylko znakiem mianownika – w obu przypadkach w mianowniku mamy dodatnią różnicę między częstotliwością źródła nieruchomego \(f_z\) i poruszającego się  \(f\). Możemy oba wzory sprowadzić do jednego, w którym w mianowniku będzie wartość bezwzględna różnicy częstotliwości \(|f - f_z|\):

(10) $$v =\frac{f v_z}{|f-v_z|}$$
po przekształceniu (10) mamy: 

(11) $$f v_z =v|f-f_z|$$

Wprowadźmy oznaczenia: \(Y= f v_z,\)  \(X=|f-f_z|,\) \(v=a\)

Wzór (11) przedstawiliśmy w postaci funkcji liniowej:  \(Y=a X\) gdzie współczynnik kierunkowy prostej \(a\) jest szukaną prędkością dźwięku.

Wykonajmy wykres we współrzędnych \(XY\) (Rys. 3), wykorzystując wszystkie wyniki pomiarów dla źródła dźwięku zbliżającego się i oddalającego od detektora. Do punktów pomiarowych na wykresie dopasujmy prostą tak, aby przechodziła jak najbliżej wszystkich punktów pomiarowych.

Mierząc kąt nachylenia prostej do osi \(X\) i obliczając tangens tego kąta, otrzymamy współczynnik 
kierunkowy prostej, a tym samym prędkość dźwięku w powietrzu.
Podając obliczoną prędkość dźwięku, nie zapomnij o jednostkach!