Cel ćwiczenia
Celem ćwiczenia jest zbadanie efektu Halla.
Wstęp
Siła Loretza
Na ładunek elektryczny poruszający się w polu magnetycznym w kierunku prostopadłym do linii pola magnetycznego działa siła, zwana siłą Lorentza. Jest ona skierowana prostopadle do kierunku prędkości ładunku i do linii pola magnetycznego, a jej wartość jest proporcjonalna do wartości ładunku q, prędkości v i indukcji magnetycznej B (Rys.1).
| (1) | \(F=qvB\) |
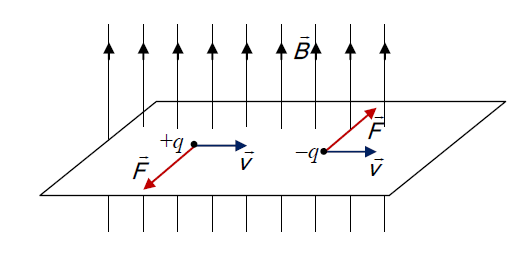 Rys.1. Siła Lorentza działająca na ładunek punktowy q poruszający się z prędkością V w kierunku prostopadłym do wektora indukcji magnetycznej B
Rys.1. Siła Lorentza działająca na ładunek punktowy q poruszający się z prędkością V w kierunku prostopadłym do wektora indukcji magnetycznej B
| Przepływ prądu polega na ruchu ładunków pod wpływem przyłożonego napięcia. Jeśli zatem umieścimy przewodnik z prądem w polu magnetycznym prostopadłym do kierunku przepływu prądu, nośniki prądu (elektrony swobodne) będą spychane przez siłę Lorentza w stronę jednej ze ścianek przewodnika. Skutkiem tego na ściankach przewodnika powstanie różnica potencjałów, zwana napięciem Halla, w kierunku prostopadłym do kierunku przepływu prądu. | Zjawisko to zaobserwował E. H. Hall w 1879 r. jeszcze przed odkryciem elektronu |
 Rys.2. Zjawisko Halla
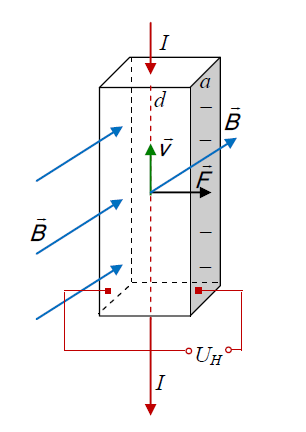
Rys.2. Zjawisko Halla
Kierunek przepływu prądu I wskazują czerwone strzałki. Ujemne nośniki prądu (elektrony) poruszają się z prędkością \(\overrightarrow{v}\) skierowaną przeciwnie do kierunku przepływu prądu. Kierunek wektora indukcji magnetycznej \(\overrightarrow{B}\) wskazują niebieskie strzałki. Siła Lorentza \(\overrightarrow{F}\) działająca na elektrony spycha je w prawo i na prawej ściance przewodnika zbiera się ładunek ujemny. Ładunek ten wytwarza poprzeczne pole elektryczne, które przeciwstawia się procesowi ich dalszego gromadzenia się. W rezultacie następuje stan równowagi, kiedy działająca na ładunki siła Lorentza będzie zrównoważona przez siłę skierowaną w przeciwną stronę i pochodzącą od wytworzonego przez zgromadzone elektrony pola elektrycznego \(\overrightarrow{E}\), które nazywamy polem Halla. Ta siła równa jest iloczynowi pola Halla i ładunku: \(F=e E\) zatem
| (2) | \(eE=evB\) |
| (3) | \(E=\frac{U_h}{d}\) |
Różnica potencjałów \(U
Natężenie pola elektrycznego możemy wyrazić jako iloraz różnicy potencjałów między lewą i prawą ścianką \(U_h\)przez odległość między ściankami \(d\):
_h\) odpowiadająca stanowi równowagi nosi nazwę napięcia Halla. Podstawiając to wyrażenie do wzoru (2) otrzymamy wzór na wartość napięcia Halla.
| (4). | \(U_h=dvB\) |
Prędkość \(v\), z jaką przenoszony jest ładunek podczas przepływu prądu nazywamy prędkością dryfu lub prędkością unoszenia. Można tę wielkość wyrazić przez natężenie prądu \(I\).
| (5). | \(v=\frac{I}{adne}\) |
Gdzie \(a\) i \(d\) to wymiary poprzeczne przewodnika, \(n\) jest liczbą nośników prądu w jednostce objętości (koncentracja), \(e\) to ładunek nośnika. Łącząc wzory (4) i (5) otrzymamy:
| (6). | \(U_h=\frac{IB}{ane}\) |
Opis układu pomiarowego
Zestaw pomiarowy do badania efektu Halla składa się z
- sterowanego zasilacza do sterowania prądem hallotronu
- sterowanego zasilacza do sterowania natężeniem indukcji magnetycznej
- układów przelączających kierunki prądów halloteronu i elektromagnesu
- hallotronu półprzewodnikowego
- elektromagnesu
- miernika napięcia Halla
- komputera sterującego
Poniższy rysunek ilustruje schemat układu pomiaru charakterystyk prądowo napięciowych.
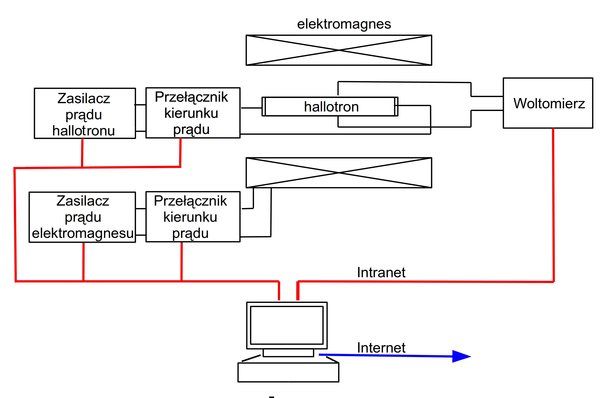 Rys.3 Schemat układu do pomiaru efektu Halla
Rys.3 Schemat układu do pomiaru efektu Halla
 Rys.4. Stanowisko do badania efektu Halla
Rys.4. Stanowisko do badania efektu Halla
Wykonanie ćwiczenia
Po zalogowaniu się do Laboratorium przyciskiem Podłącz wybieramy możemy wybrać mod pomiaru. Możemy mierzyć zależność napięcia Halla od prądu przepływającego przez próbkę przy ustalonej wartości pola indukcji magnetycznej lub zależność napięcia Halla od pola magnetycznego przy ustalonej wartości prądu przepływającego przez próbkę.
W pierwszym przypadku wybieramy
- początkową wartość prądu
- końcową wartość prądu
- skok przyrostu prądu
- wartość indukcji pola magnetycznego
W drugim przypadku wybieramy
- początkową wartość indukcji pola magnetycznego
- końcową wartość indukcji pola magnetycznego
- skok przyrostu indukcji pola magnetycznego
- wartość prądu przepływającego przez próbke.
Po naciśnięciu przycisku Start rozpoczyna się cykl pomiaru. Komputer sterujący ustawia początkowe wartości parametrów, które po wykonaniu pomiaru napięcia Halla, zmienia o wartość zadanego skoku przyrostu. Poprzez sieć internetową wyniki pomiarów są sukcesywnie przesyłane na komputer użytkownika i wyświetlane na ekranie monitora w postaci wykresu zależności wartości napięcia Halla od zmienianego parametru. W dowolnej chwili można przerwać pomiar, zapisać dane na dysku, zmienić parametry i ponownie uruchomić pomiary.
Opracowanie wyników
1. Korzystając ze wzoru (4), wyznacz prędkość unoszenia elektronów \(v\). Sporządź wykres, w którym na osi poziomej jest iloczyn \(dB\), a na osi pionowej \(U_h\). Przez punkty doświadczalne przeprowadź prostą. Tangens kąta nachylenia tej prostej do osi poziomej będzie równy prędkości unoszenia.
Uwaga na jednostki! Jeśli wszystkie wielkości będą wyrażone w jednostkach układu SI, to prędkość otrzymamy w m/s.
2. Porównaj prędkość unoszenia z prędkościami termicznymi elektronów. Skorzystaj ze wzoru na średnią energię kinetyczną ruchów termicznych elektronów swobodnych: $$E_k=\frac{kT}{2}$$ gdzie \(k = 1,38*10^{-23}\) \(J/K\) (stała Boltzmanna), T temperatura w skali bezwzględnej (można przyjąć \(T = 300K\)). Masa elektronu: \(m_e = 9,1*10^{-31}\) \(kg\).
3. Korzystając ze wzoru (6) wyznacz koncentrację nośników prądu \(n\). Przekształćmy wzór (6) do postaci: \(IB=nae U_h\)
Posłuż się wykresem, w którym na osi poziomej będzie \(aeU_h\), a na osi pionowej \(IB\) . Współczynnik kierunkowy prostej przeprowadzonej przez punkty doświadczalne, to właśnie szukana koncentracja \(n\).