E-fizyka | Witamy!

Cel ćwiczenia

Celem ćwiczenia jest poznanie praw rządzących rozpływem prądów w obwodach elektrycznych.

Wstęp

Obwód elektryczny to układ elementów biernych (takich jak oporniki, kondensatory, czy indukcyjności) oraz elementów czynnych (źródła prądu np. baterie, akumulatory czy prądnice), które tworzą układ zamknięty. W takim układzie może przepływać prąd elektryczny. W połowie XIX wieku Gustaw Kirchhoff sformułował prawa rządzące zależnościami pomiędzy prądami i wartościami elementów czynnych i biernych.

Pierwsze prawo Kirchhoffa mówi że jeśli w pewnym punkcie (zwanym węzłem) połączone są przewody przez które płynie prąd, to suma natężeń prądów wpływających do tego węzła jest równa sumie natężeń prądów z niego wypływających. Jest to przejaw zasady zachowania ładunku - ładunek znikąd się nie tworzy i nie zanika. Inaczej można powiedzieć że jeśli prąd elektryczny tworzą przepływające elektrony, to tyle ile elektronów wpłynie do węzła to tyle samo musi wypłynąć. Poniższy rysunek przedstawia jeden węzeł obwodu, w którym połączonych jest pięć przewodników z prądem.

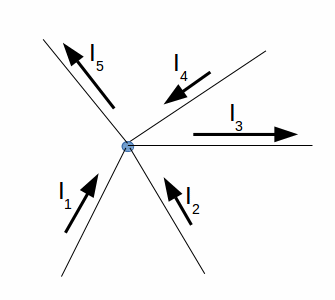Rys.1. Węzeł obwodu

Możemy napisać:

1)$${I_1+I_2+I_4}=I_3+I_5$$

Formalizując, jeśli ze znakiem „+” napiszemy prądy wpływające do węzła, zaś ze znakiem „-” prądy wypływające to możemy zapisa:

2)$$\sum{I_{n+}}-\sum{I_{n-}}=\sum{I_n}=0$$

Drugie prawo Kirchhoffa odnosi się do zamkniętych obwodów z prądem. Układ zamknięty będący składnikiem większego układu elektrycznego nazywany jest oczkiem układu. Poniższy rysunek przedstawia przykładowy obwód, w którym elementami biernymi są tylko opory. Schemat ten ilustruje układ połączonych szeregowo baterii o sile elektromotorycznej $\mathcal{E}$ i oporze wewnętrznym $R_w$ oraz opornika o oporze $R$. Na obu oporach następuje spadek napięcia, odpowiednio $U_1$ i $U_2$.

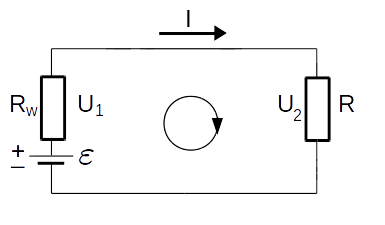Rys.2. Oczko obwodu elektrycznego.

Drugie prawo Kirchhoffa mówi że suma spadków napięcia w oczku obwodu jest równa sumie sił elektromotorycznych.

W naszym przypadku możemy napisać:

$$ U_1+U_2=\mathcal{E} $$

oraz uogólniając:

$$ \sum{U_i}=\sum\mathcal{E_j} $$

W połączeniu z prawem Ohma, prawa Kirchhoffa umożliwiają wyznaczenie wszystkich prądów i spadków napięcia w układzie.

Obliczmy wartość natężenia prądu w naszym układzie. Stosując prawo Ohma, spadek napięcia $U_1= I\cdot{R_w}$, zaś $U_2=I\cdot{R}$. Z drugiego prawa Kirchhoffa wynika zależność:

$ I\cdot{R_w}+I\cdot{R}=\mathcal{E}$, skąd: $I=\mathcal{E}/(R_w+R)$

Kierunek strzałki wewnątrz naszego oczka (zgodny z ruchem wskazówek zegara) został wybrany zgodnie z kierunkiem przepływu prądu w obwodzie (od plusa do minusa baterii), ale może to być kierunek dowolny. Trzeba tylko stosować konwencję że jeśli kierunek przepływu prądu zgadza się z kierunkiem strzałki wówczas spadek napięcia występujący w powyższej sumie (wzór 4) piszemy ze znakiem dodatnim, zaś jeśli są to kierunki przeciwne -ze znakiem ujemnym.

Opis układu pomiarowego

Schemat układu pomiarowego ilustruje Rys. 3. Zestaw składa się z bloku zasilania, układów pomiaru prądu, sterowanych przełączników i zestawu oporników.

Układ pomiarowy składa się z trzech oporników o oporności $100 \Omega$ podłączonych jedną końcówką do wspólnego węzła (oznaczonego literą Z na rysunku), a drugą do zasilacza napięciowego. W każdej gałęzi zamontowano miliamperomierz.

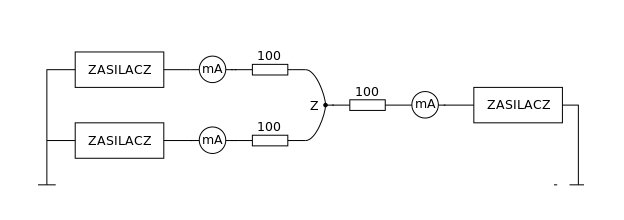Rys.3. Schemat układu pomiarowego.

Zasilacze posiadają możliwość regulacji napięcia wyjściowego. Po ustawieniu napięć wyjściowych zasilaczy można dokonać pomiaru prądów płynących przez każdy opornik - miliamperomierze włączone są szeregowo z opornikami, więc mierzymy prądy wpływające do wspólnego węzła Z.
Zgodnie z prawem Kirchhoffa suma prądów wpływających do węzła i wypływających z niego wynosi 0.

Wykonanie ćwiczenia

Po zalogowaniu się do Laboratorium przyciskiem Podłącz wprowadzamy napięcia wyjściowe zasilaczy $ U_1, U_2 $ i $U_3$. Po naciśnięciu przycisku Start rozpoczyna się pomiar. Komputer sterujący ustawia wybrane napięcia na wyjściach zasilaczy, po czym wykonuje pomiar prądów za pomocą miliamperomierzy. Po zakończeniu pomiaru prądów (zmierzone wartości pojawiają się na ekranie) można wprowadzić nowe nastawy dla zasilaczy i rozpocząć kolejny cykl pomiarowy. W dowolnej chwili można przerwać pomiar, zapisać dane na dysku, zmienić parametry i ponownie uruchomić pomiary.

Opracowanie wyników

Zapisane wyniki pomiarów przenosimy do tabelki:

Napięcie $U_1 [V]$	Napięcie $U_2 [V]$	Napięcie $U_3 [V]$	Prąd $I_1 [mA]$	Prąd $I_2[mA]$	Prąd $I_3 [mA]$	Suma prądów $I_1+I_2+I_3 [mA]$
$U_{11}$	$U_{21}$	$U_{31}$	$I_1(U_{11})$	$I_2(U_{21})$	$I_3(U_{31})$
$U_{12}$	$U_{22}$	$U_{32}$	$I_1(U_{12})$	$I_2(U_{22})$	$I_3(U_{32})$
...	...	...	...	...	...

W każdym przypadku obliczyć sumę prądów $I_1, I_2, I_3 $ i sprawdzić że wynosi zero w granicach niepewności pomiarowych.
Niepewność pomiaru prądu przyjąć 1% zakresu pomiarowego + 2dgt.

Napięcie \(U_1 [V]\)	Napięcie \(U_2 [V]\)	Napięcie \(U_3 [V]\)	Prąd \(I_1 [mA]\)	Prąd \(I_2[mA]\)	Prąd \(I_3 [mA]\)	Suma prądów \(I_1+I_2+I_3 [mA]\)
\(U_{11}\)	\(U_{21}\)	\(U_{31}\)	\(I_1(U_{11})\)	\(I_2(U_{21})\)	\(I_3(U_{31})\)
\(U_{12}\)	\(U_{22}\)	\(U_{32}\)	\(I_1(U_{12})\)	\(I_2(U_{22})\)	\(I_3(U_{32})\)
...	...	...	...	...	...