Cel ćwiczenia
Celem ćwiczenia jest badanie prawa zachowania energii w polu grawitacyjnym, a także zapoznanie się z prawami rządzącymi ruchem obrotowym.
Wstęp
Wahadło Maxwella
Wahadło Maxwella to duży krążek zawieszony na linkach nawiniętych na jego cienką oś. Gdy pozwolimy mu swobodnie opadać, krążek zacznie kręcić się wokół swojej osi, a opadanie będzie znacznie wolniejsze niż w przypadku swobodnego spadku. Po całkowitym rozwinięciu linek krążek, wirując, wznosi się do góry. Cały cykl powtarza się wielokrotnie.
Ruch wahadła Maxwella ilustruje prawo zachowania energii mechanicznej w polu grawitacyjnym. W najwyższym punkcie wahadło ma energię potencjalną względem najniższego położenia
Gdy wahadło opada, energia potencjalna zamienia się na energię kinetyczną. Krążek bierze udział w dwóch ruchach: ruchu postępowym środka masy w dół i ruchu obrotowym wokół osi krążka. Energia kinetyczna jest więc sumą energii kinetycznej ruchu postępowego:
(1) $$E_{k_{post}}=\frac{mv^2}{2}$$
i energii kinetycznej ruchu obrotowego:
(2)$$E_{k_{obr}} = \frac{I \omega^2}{2},$$
a (\(v\)) obiektu poruszającego się po okręgu zależy od promienia \((R)\) oraz częstotliwości \(\nu\) obrotów. Jeśli obiekt wykona w ciągu jednej sekundy \(\nu\) obrotów, to droga jaką pokona w tym czsie w
gdzie \(m\) – masa,\( v\) – prędkość środka masy wahadła, \(I\) – moment bezwładności krążka, \(\omega\)- prędkość kątowa wirującego krążka.
Podczas opadania w każdej chwili całkowita energia kinetyczna jest równa utraconej energii potencjalnej \(E_p =mgh'\), gdzie \(m\) to masa wahadła, \(g\) – przyspieszenie ziemskie, \(h’\) – wysokość, o jaką wahadło opuściło się od najwyższego położenia (Rys. 1).
(3)$$mgh' = \dfrac{m v^2}{2}+\dfrac{I \omega^2}{2},$$
Podczas opadanie energia potencjalna zamienia się na energię kinetyczną ruchu postępowego i obrotowego.
Rys. 1. Opadające wahadło przebyło drogę \(h’\) od najwyższego położenia, długość linki wynosi \(H\), wysokość nad najniższym położeniem – \(h\).
Gdy wahadło osiągnie swoje najniższe położenia, siła sprężystości linek wyhamuje ruch postępowy wahadła. Energia kinetyczna ruchu postępowego zaniknie i ulegnie rozproszeniu w postaci wydzielonego ciepła. Jednak energia kinetyczna ruchu obrotowego pozostanie niezmieniona – krążek nadal wirując, wznosi się do góry, nawijając linki na oś. Teraz energia kinetyczna zamienia się na energię potencjalną. W końcu energia kinetyczna stanie się równa zeru i wahadło znajdzie się w najwyższym punkcie. Jednak część energii kinetycznej (energia kinetyczna ruchu postępowego) została utracona podczas hamowania w najniższym położeniu, więc wysokość, na jaką wahadło się wzniesie, będzie nieco mniejsza niż w poprzednim cyklu. Po dłuższym czasie ruch wahadła ustanie.
Opis układu pomiarowego
Układ pomiarowy składa się z ciężkiego mosiężnego walca zamocowanego na długiej metalowej cienkiej osi (Rys.1). Do osi tej przymocowana jest linka, której drugi koniec połączony jest z ramą. W stanie początkowym walec znajduje się w spoczynku zawieszony na linkach. Po uruchomieniu ćwiczenia mechanizm napędu powoduje obrót walca. Obracający się walec nakręca linkę na osi a jednocześnie cały układ podnosi się do góry. Po osiągnięciu zadanej wysokości układ napędu zostaje odłaczony od walca i pod wpływem siły ciężkości walec zaczyna opadać na dół jednocześnie obracając się wokól osi. Do pomiaru prędkości obrotowej służy przetwornik umieszczony na osi obrotu walca. Przetwornik ten podaje liczbę impulsow w jednostce czasu, zależną od prędkości obrotowej walca. Analiza liczby zliczeń umożliwia wyznaczenie wysokości na której aktualnie znajduje się oś oraz prędkości liniowej. Wartości wysokości, prędkości liniowej oraz prędkości obrotowej podawane są w funkcji czasu.
 Rys.1. Zestaw pomiarowy
Rys.1. Zestaw pomiarowy
Do policzenia momentu bezwładności koła Maxwella potrzebne są wymiary krążka i pręta na który nawija się linka oraz masa właściwa (gęstośc) materiału z którego są one wykonane. Parametry geometryczne kola przedstawia poniższy rysunek:
Krążek wykonany jest z mosiądzu o gęstości \(8500g/cm^2\). Pręt ma wymiary: średnica \(D=10mm\) i dlugość \(L=285 mm\). Pręt wykonany jest z żelaza o gęstości \(7875 g/cm^2\).
Wykonanie ćwiczenia
Po zalogowaniu się do Laboratorium przyciskiem Podłącz wybieramy początkową wysokość walca. Po naciśnięciu przycisku Start rozpoczyna się cykl pomiaru. Poprzez sieć internetową wyniki pomiarów są sukcesywnie przesyłane na komputer użytkownika i wyświetlane na ekranie monitora w postaci wykresu zależności prędkości liniowej krążka \(v\) oraz prędkości obrotowej \(\omega\) i wysokości \(h’\) w funkcji czasu pomiaru. W dowolnej chwili można przerwać pomiar, zapisać dane na dysku, zmienić parametry i ponownie uruchomić pomiary.
Opracowanie wyników
Wykonaj wykresy zależności prędkości liniowej i kątowej od czasu na jednym rysunku. Patrząc na wykresy, określ w jakim punkcie znajduje się wahadło i w którą stronę się porusza w kolejnych momentach. Porównaj wynik z zapisaną wysokością dla tych momentów.
Sprawdzenie prawa zachowania energii.
Dla każdej serii danych (wysokość, prędkość liniowa, prędkość kątowa w jednym momencie) oblicz:
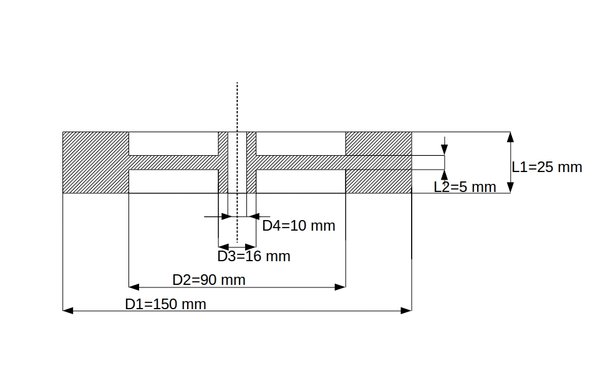 Rys.2. Wymiary koła Maxwella
Rys.2. Wymiary koła Maxwella
|
|
Przykładowy wykres energii kinetycznej, potencjalnej i całkowitej.
Jaką część całkowitej energii kinetycznej stanowi energia ruchu postępowego, która tracona jest w każdym cyklu ruchu wahadła?
Musimy najpierw znaleźć związek między prędkością środka masy \(v\), a prędkością kątową krążka \(\omega\). Przeanalizujmy Rys.2, przedstawiający linkę odwijającą się na osi krążka, który wirując porusza się w dół. Jaką drogę \(s\) przebędzie środek masy wahadła, gdy promień \(r\) zakreśli kąt \(\alpha\)? Widzimy, że droga \(s\) równa jest łukowi opartemu na kącie środkowym \(\alpha\). Związek między tymi wielkościami to:
(4)$$ s=\alpha r$$
Wynika z tego związek między prędkością liniową środka masy \(v\) i prędkością kątową \(\omega\):
(5)$$v=\omega r$$ lub $$\omega =\frac{v}{r}$$
Rys. 3 Ilustracja zależności między prędkością liniową środka masy \(v\) i prędkością kątową \(\omega\).
Jeśli promień krążka oznaczymy jako \(R\), a promień osi \(r\), to energia kinetyczna ruchu obrotowego będzie równa:
(6) $$E_{k_{obrt}}=\frac{1}{2}I\omega^2=\frac{1}{2}\frac{mR^2}{2}\frac{v^2}{r^2}=\frac{mv^2}{2}\frac{1}{2}=E_{k_{post}}\frac{1}{2}\frac{R^2}{r^2}$$
(7) $$\frac{E_{k_{obrt}}}{E_{k_{post}}}=\frac{1}{2}(\frac{R}{r})^2$$
Wstawiając znane wartości \(R\) i \(r\) do wzoru (7), oblicz, ile razy energia kinetyczna ruchu obrotowego jest większa niż energia kinetycznej ruchu postępowego.
Odpowiedz na pytanie, dlaczego wahadło tak wolno opada w dół?
Przy pobliczaniu niepewności wyznaczenia energii można przyjąć niepewność określenia położenia \(\Delta h= 1mm\), niepewność określenia czasu \(\Delta t= 10^{-5} sek\), niepewności wynaczenia parametrów geometrycznych koła Maxwella \(\Delta D1=0,4 mm\), \(\Delta D2=0,2 mm\), \(\Delta D3=0,05 mm\), \(\Delta D4=0,05 mm\), \(\Delta L2=0,05 mm\), \(\Delta D3=0,1 mm\), \(\Delta D=0,05 mm\), \(\Delta L=0,5 mm\).