3.5. Doświadczenia „Radiacja”
Wykonamy teraz dwa doświadczenia, które na pozór mają niewiele wspólnego z fizyką jądrową: zbadamy losowe zjawisko przewracania się kapsli oraz zjawisko stygnięcia wody. Okaże się, że uzyskane w tych doświadczeniach wyniki mają wspólny opis matematyczny, tożsamy z prawem zaniku promieniotwórczego. Dzieje się tak dlatego, że te trzy różne w swej istocie zjawiska podlegają takiemu samemu prawu statystycznemu. Każdy opis matematyczny zjawiska musi opierać się na określonym prawie fizycznym. W sprawozdaniach z tych doświadczeń napisz, które prawo statystyczne jest wspólne dla tych trzech różnych zjawisk.
Przeprowadzenie tych doświadczeń pozwoli nam lepiej zrozumieć prawo zaniku promieniotwórczego próbki promieniotwórczych jąder atomowych oraz powiązane z nim pojęcie czasu połowicznego zaniku, poznane w rozdziale 3.4. Prawo rozpadu promieniotwórczego.
Przekonamy się wreszcie, że przebieg wszystkich tych procesów zachodzi według takiego samego prawa wykładniczego, którego wyprowadzenie podaliśmy w dodatku do poprzedniego rozdziału, przeznaczonym dla uczniów szczególnie zainteresowanych matematyką.
„Prawo promieniowania” a statystyczny zanik liczby nieodwróconych kapsli
Do przeprowadzenia doświadczenia potrzebne jest około stu jednakowych kapsli (nakrętek po napojach). Stanowią one „próbkę” obiektów mogących się „przemienić” – tutaj: odwrócić dnem do góry.
Kapsle ułóż na desce dnem do dołu (il. 3.51b). Przygotuj wolny obszar podłogi o rozmiarze rzędu metr na metr; obszar ten warto odgrodzić, by kapsle nie uciekały zbyt daleko.
Wysyp „z impetem” kapsle z deski na podłogę. Następnie zbierz kapsle z podłogi, odkładając z powrotem na deskę tylko te, które upadły dnem do dołu; należy je policzyć i zapisać ich liczbę . Te zaś kapsle, które się odwróciły i upadły dnem do góry (il. 3.51a), odłóż na bok – uznajemy, że „wypromieniowały” one z próbki.

Powyższe czynności powtórz wielokrotnie, każdorazowo zliczając liczbę kapsli, które się nie odwróciły po kolejnym rzucie. Połóż je na desce przed następnym rzutem.
Wyniki zliczeń umieść w tabeli wykonanej wg poniższego wzoru (il. 3.52). Zapełnij pierwsze dwie kolumny tabeli (Kolejny numer rzutu i ).
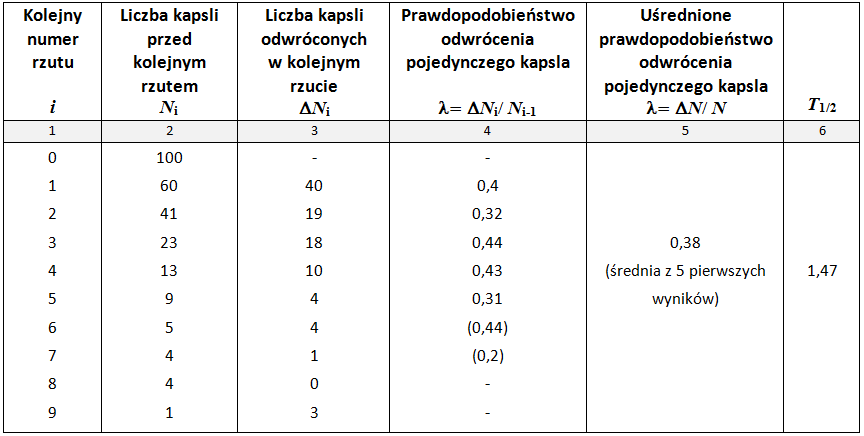
W celu obliczenia prawdopodobieństwa odwrócenia kapsla najpierw wypełnij 3. kolumnę tabeli; oblicz – liczbę kapsli, które odwróciły się w -tym rzucie. Następnie oblicz prawdopodobieństwa odwrócenia pojedynczego kapsla w każdym rzucie i wypełnij 4. kolumnę tabeli.
Wykonaj wykres zależności od . Przykładowy wykres przedstawia il. 3.54.
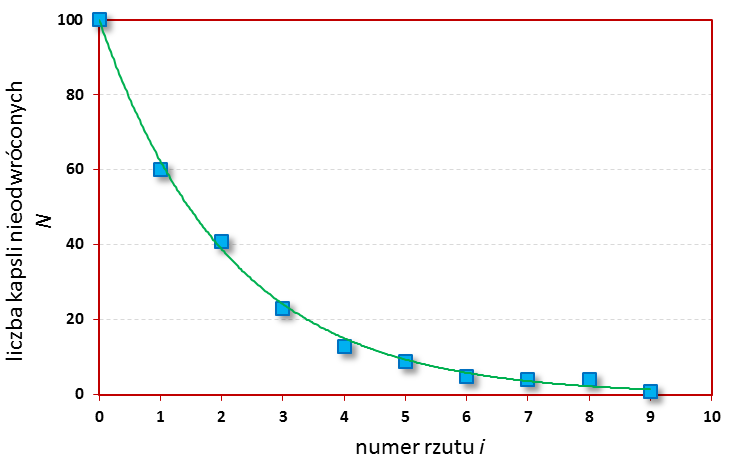
Zwróćmy uwagę na trzy istotne cechy wykresu. Te same cechy ma wykres zależności między czasem a liczbą jąder, które nie uległy przemianie w zjawisku rozpadu promieniotwórczego, opisanemu w rozdziale 3.4. Prawo rozpadu promieniotwórczego.
- Uzyskano wyniki wskazujące na zależność malejącą.
- Wykres nie jest linią prostą – liczba nieodwróconych kapsli maleje nieliniowo wraz z liczbą rzutów.
- Nie można przewidzieć żadnej określonej ilości rzutów, po której liczba nieodwróconych kapsli osiągnie wartość .
Pierwsza cecha jest oczywista: w warunkach doświadczenia nie może przybywać nieodwróconych kapsli.
Ciekawa jest natomiast druga cecha wykresu. Związana jest ona z pojęciem prawdopodobieństwa odwrócenia się kapsla. W 3. kolumnie tabeli pokazano wielkość – liczbę kapsli, które odwróciły się w -tym rzucie. Z kolei wielkość to liczba kapsli przed -tym rzutem, które mogły się odwrócić w tym rzucie.
W celu obliczenia prawdopodobieństwa odwrócenia kapsla zastosowaliśmy wzór (3.16) wyrażający stosunek liczby kapsli, które się odwróciły, do liczby kapsli, które potencjalnie odwrócić się mogły.
Doświadczalne wartości zamieszczono w 4. kolumnie tabeli (tabela na il. 3.53). Widzimy, że wartości te są w przybliżeniu jednakowe, czego należało oczekiwać.
To, że nie są dokładnie jednakowe, raz są nieco większe, raz nieco mniejsze, nie wynika z niepewności pomiarowej, lecz z losowego charakteru odwracania się kapsli i z niewielkiej próbki statystycznej, jaką dysponujemy w tym doświadczeniu. Oczywiście nie ma powodu przypuszczać, by prawdopodobieństwo odwrócenia się kapsla zależało od tego, ile rzutów przeszedł pojedynczy kapsel bez odwrócenia. Na podstawie pięciu pierwszych rzutów możemy wyznaczyć średnią wartość .
Wzór (3.16), odpowiednio przekształcony, w którym przyjęto, że wartość jest taka sama:
pokazuje, że liczba odwróconych kapsli w kolejnych rzutach nie jest stała, ale jest proporcjonalna do aktualnej, malejącej liczby nieodwróconych kapsli, na co wskazuje kształt wykresu z il. 3.54.
Na koniec zwróćmy uwagę na istotną, choć pozorną różnicę między doświadczeniem z kapslami a zjawiskiem zaniku próbki promieniotwórczych jąder atomowych – to kwestia odcinka czasowego . W poprzednim rozdziale czas ten spowodował konieczność rozróżnienia stałej rozpadu i prawdopodobieństwa rozpadu. W przedstawionym powyżej rozumowaniu pojęcia te utożsamiono. Czy to postępowanie jest uprawnione? Tak, gdyż w doświadczeniu z kapslami rolę „odcinka czasu” odgrywają kolejne rzuty. „Czasu trwania” tych rzutów nie można regulować, więc liczba zarejestrowanych odwróceń zależy tylko od właściwości kapsli. Można jednak przypisać kolejnym rzutom interpretację zbliżoną do czasu – w zadaniu 3. wyznaczysz „czas połowicznego zaniku” próbki kapsli.
Stygnięcie cieczy (materiał nadobowiązkowy)
Przeprowadzając doświadczenie, przekonamy się, że spadek temperatury rozgrzanego ciała zachodzi według takiego samego prawa wykładniczego, co zanik promieniowania radioaktywnego (wyprowadzenie wzoru znajduje się w końcowej części tego rozdziału):
gdzie: – temperatura rozgrzanego ciała, – temperatura otoczenia (temperatura końcowa po ostygnięciu ciała), – temperatura początkowa rozgrzanego ciała, – czas, – czas, po którym temperatura cieczy osiąga wartość będącą średnią arytmetyczną i .
Do przeprowadzenia doświadczenia wystarczy termometr o zakresie skali od do , szklanka z podgrzaną wodą i stoper lub zegarek. Jako alternatywny przyrząd do sygnalizacji upływu czasu może być zastosowany minutnik.
Do szklanki wlej wodę zagrzaną do temperatury nieco wyższej niż i wstaw termometr (il. 3.55).
Ustaw szklankę w miejscu nieprzewiewnym, aby warunki stygnięcia były cały czas jednakowe, i włącz stoper. Notuj wskazania termometru np. co 5 minut (do sygnalizacji upływu czasu możesz zastosować minutnik). Pomiary możesz wykonać bardziej precyzyjnie, jeżeli sfilmujesz przebieg doświadczenia za pomocą kamery (lub komórki) i przy odtwarzaniu filmu zatrzymasz odpowiednie klatki filmu.
Wyniki pomiarów zapisz w kolumnach 2, 3 i 5 tabeli wykonanej wg poniższego wzoru (il. 3.56). Jednocześnie stopniowo wypełniaj kolumnę 4 – „nadwyżka temperatury” wody nad temperaturą otoczenia.

Określ niepewności pomiarowe: temperatury – jako połowę najmniejszej podziałki , np. , czasu – przy pomiarze czasu uwzględnij czas reakcji na sygnalizację czasu oraz niezbędny czas potrzebny do odczytu wskazań stopera i termometru, np. . Dane te zapisz; posłużą ci one do wykreślenia prostokątów niepewności pomiarowych.
Korzystając z danych z kolumn 4 i 5 tabelki pomiarów, wykonaj wykres punktowy zależności nadwyżki temperatury wody ( ) od czasu stygnięcia (il. 3.57).
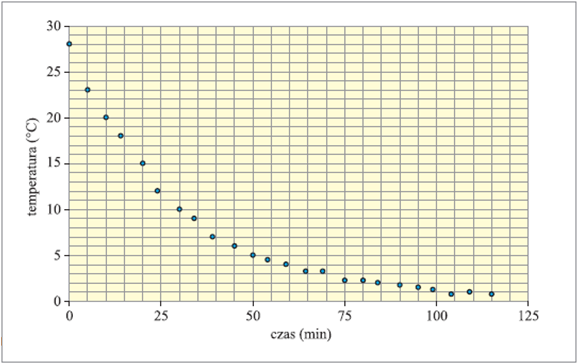
Każdy punkt otocz prostokątem niepewności pomiarowych wykonanych według il. 3.58.
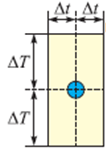
Następnie „od ręki” wykreśl krzywą, która będzie przebiegać przez obszary wszystkich prostokątów niepewności pomiarowych (il. 3.59). Uwaga: krzywa ta nie powinna być łamaną przebiegającą od punktu do punktu, powinna być „gładka” – wystarczy, że będzie przechodzić przez wspomniane prostokąty. Dzięki temu będzie lepiej odpowiadać rzeczywistemu przebiegowi procesu stygnięcia, gdyż proces ten nie przebiega według krzywej łamanej.
Na koniec zaznacz na wykresie linie poziome połowicznego zaniku nadwyżki temperatury wody nad temperaturą otoczenia (w skrócie: linie połowicznego zaniku temperatury) przebiegające jak na il. 3.60.
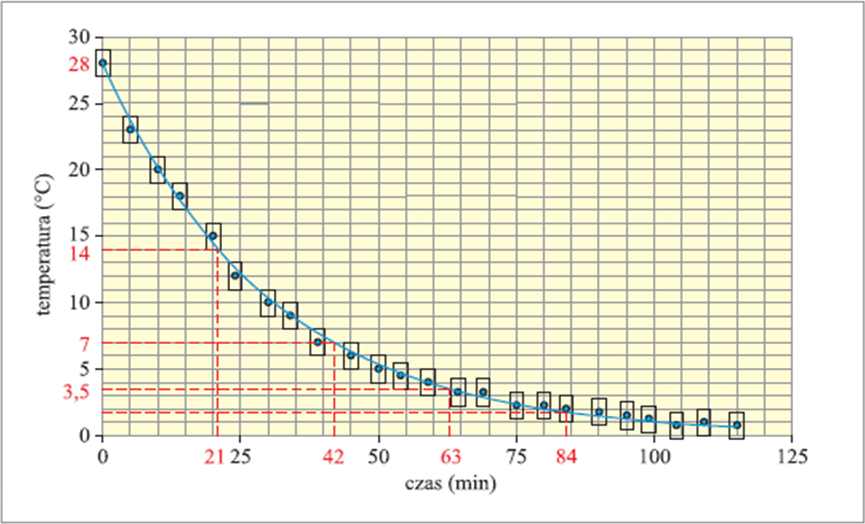
Pierwsza linia przecina oś temperatury w połowie odcinka łączącego punkt temperatury początkowej i punkt początkowy układu współrzędnych .
Druga linia pozioma odcina następną połowę połowy tego odcinka itd. (na przykładowym wykresie zaznaczono cztery takie poziome linie).
Linie połowicznego zaniku temperatury przecinają krzywą w określonych punktach, z których należy poprowadzić pionowe linie. Linie te na osi czasu odetną odcinki, przy których nadwyżka temperatury nad otaczającą maleje o połowę. Przekonaj się, że te wszystkie odcinki są sobie równe (z dokładnością do niepewności pomiarowych); to właśnie jest czas połowicznego stygnięcia (z przykładowego wykresu – il. 3.60 otrzymano ). Zauważ, że krzywa ta ma identyczny charakter co krzywa rozpadu promieniotwórczego, gdzie odpowiada okresowi połowicznego rozpadu.
Zapisz swoje spostrzeżenia i wnioski z przeprowadzonego doświadczenia.
Stygnięcie cieczy – wyprowadzenie wzorów (materiał nadobowiązkowy)
Gdy ogrzejemy ciało do temperatury wyższej od temperatury otoczenia i pozwolimy mu swobodnie stygnąć, to jego temperatura będzie stopniowo się obniżać, zbliżając się asymptotycznie do temperatury otoczenia . Tak zachowywała się woda w doświadczeniu Stygnięcie cieczy.
Pokażemy, że temperatura będzie obniżać się podobnie, jak zanika liczba aktywnych jąder w preparacie promieniotwórczym, czyli zgodnie z krzywą rozpadu promieniotwórczego (il. 3.50).
Jeżeli ciało ma temperaturę , to całkowite ciepło odprowadzone do otoczenia w trakcie stygnięcia wyniesie:
Przekaz cieplny energii od ciała cieplejszego do otoczenia zachodzi stopniowo. W określonym odcinku czasu do otoczenia zostanie przekazane ciepło , z czym związana będzie zmiana temperatury ciała o . Pamiętając więc, że , możemy zapisać:
gdzie – masa ciała, – jego ciepło właściwe. W drugiej równości wykorzystano oczywisty fakt, że zmiana temperatury ciała jest równa zmianie różnicy między jego temperaturą a temperaturą otoczenia, gdyż ta ostatnia jest stała.
Ciepło można wyrazić bezpośrednio przez różnicę między chwilową temperaturą ciała a temperaturą otoczenia za pomocą prawa stygnięcia, sformułowanego przez Newtona. Stwierdza ono, że jest proporcjonalne do różnicy oraz do czasu :
gdzie – stały współczynnik opisujący właściwości termiczne stygnącego układu (np. jego przewodność cieplną) oraz styku układu z otoczeniem (np. przewodność cieplną ścianek naczynia, rozmiar tych ścianek). Współczynnik ten wyznacza się doświadczalnie. Warto tu dodać, że prawo Newtona opisuje proces stygnięcia tym lepiej, im większy w tym procesie jest udział przewodnictwa ciepła, a mniejszy promieniowania i konwekcji.
Lewe strony wzorów (3.20) i (3.21) są takie same, możemy więc przyrównać do siebie ich prawe strony:
Po przekształceniu i zastosowaniu oznaczenia otrzymujemy:
Wzór (3.22) jest tożsamy – pod względem struktury – ze wzorem (3.9). Oznacza to, że temperatura stygnącego ciała (dokładniej: różnica między jego temperaturą a temperaturą otoczenia) zmienia się czasie tak samo, jak liczebność próbki promieniotwórczej. Można więc dla procesu stygnięcia wprowadzić pojęcie „czasu połowicznego zaniku różnicy temperatury” , analogiczne do czasu połowicznego zaniku liczebności próbki. Wniosek ten jest zgodny z wynikami doświadczenia Stygnięcie cieczy, w którym stwierdziliśmy, że zawsze po określonym odcinku czasu ciało jednakowo stygnie. W określonym czasie różnica temperatury ciała i temperatury otoczenia zmniejsza się o połowę, po czym – w kolejnym czasie – znowu o połowę, itd.
Oznaczmy początkową temperaturę stygnącego ciała przez i uogólnijmy powyższe spostrzeżenie w postaci analogicznej do wzoru (3.11):
Stąd
Otrzymaliśmy wzór określający prawo zaniku nadwyżki temperatury ciała podczas stygnięcia, wyrażony za pomocą okresu połowicznego zaniku . Wykorzystaliśmy przy tym fakt, że prawo to ma podobny charakter do prawa rozpadu promieniotwórczego.
Można wykazać, podobnie jak w wyprowadzeniu prawa rozpadu promieniotwórczego w rozdziale 3.4. Prawo rozpadu promieniotwórczego, że prawo zmiany temperatury ciała podczas stygnięcia może być wyrażone w postaci:
gdzie: – podstawa logarytmu naturalnego.
Pytania i problemy
- W komputerowym doświadczeniu obrazującym rozpad próbki promieniotwórczych jąder
atomowych przyjęto pewne założenia; zostały one podane poniżej. Zapisz przy
każdym z nich analogiczne założenie obowiązujące dla doświadczenia
z kapslami. Rozstrzygnij, czy stwierdzone podobieństwa i różnice mają
znaczenie istotne, czy tylko formalne. Przykładową wypowiedź podano dla
założenia 'a'.
- Liczebność próbki obserwujemy w umownych odstępach czasu . Wartość można dowolnie zmieniać. Rolę „odcinka czasu” odgrywają kolejne rzuty, których „czasu trwania” nie można regulować.
- Początkowa liczebność próbki .
- Przyjmiemy, że prawdopodobieństwo zajścia rozpadu pojedynczego jądra w kolejnym odstępie czasu jest iloczynem stałej rozpadu i odstępu czasu i wynosi 0,1, czyli 10%.
- Prawdopodobieństwo, o którym mowa w punkcie c, można dowolnie zmieniać.
- Jeśli jądro nie ulegnie rozpadowi w pewnym odcinku czasu , to prawdopodobieństwo jego rozpadu w następnym odstępie czasu nadal wynosi 10%.
- Wydrukuj w odpowiednim powiększeniu wykres z il. 3.54 i określ graficznie „czas połowicznego odwracania się” próbki kapsli. Wyraź ten czas w rzutach; przyjmij na potrzeby zadania, że możliwe jest wykonanie niecałkowitej liczby rzutów.
- Przeprowadź doświadczenie podobne do tego z kapslami; użyj jednak 100 prostopadłościennych klocków (pomyśl może o wykorzystaniu
cukierków odpowiedniego kształtu albo pudełek po zapałkach), 100 kostek do gry lub 100 monet. Ustal, że po każdym rzucie z próbki
eliminowane są te klocki, które upadły „na sztorc”, czyli na najmniejszą podstawę, te kostki, które upadły „jedynką do góry”,
czy te monety, które upadły „orłem w dół”.
- Zapisz wyniki doświadczenia w tabelce.
- Sporządź wykres obrazujący liczbę pozostających w próbce obiektów po każdym z rzutów. Poprowadź „od ręki” krzywą najlepiej pasującą do punktów doświadczalnych.
- Z wykresu odczytaj „czas połowicznego zaniku” próbki – jest to „liczba” rzutów, po której liczebność próbki maleje o połowę. Zwróć uwagę, że nie musi być liczbą całkowitą.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
