4.7. Prawo zachowania momentu pędu

Poprzednio omawialiśmy dwie fundamentalne zasady zachowania – zasadę zachowania pędu i zasadę zachowania energii. Obecnie zapoznasz się z następną – zasadą zachowania momentu pędu. Pozwala ona na rozwiązywanie wielu problemów fizycznych w sposób łatwy, bez konieczności analizowania ruchów indywidualnych cząstek i sił na nie działających.

Jeżeli wypadkowy moment sił działający na ciało (lub układ ciał) jest równy zeru $\vec{M}=0$ , to ze wzoru:

\vec{M}=\frac{\Delta\vec{L}}{\Delta t}

wynika, że:

\Delta\vec{L}=0\qquad czyli\qquad\vec{L}=const

( 4.60 )

Całkowity moment pędu ciała (lub układu ciał) jest więc stały. W szczególności, jeżeli mamy do czynienia z układem odosobnionym, to siły zewnętrzne są równe zeru i wypadkowy moment sił jest równy zeru. Wtedy obowiązuje równanie (4.60). Otrzymaliśmy bardzo ważny wynik – prawo zachowania momentu pędu, które brzmi:

Prawo zachowania momentu pędu należy do podstawowych praw przyrody i obok prawa zachowania pędu i prawa zachowania energii ma powszechne zastosowanie w odniesieniu do zjawisk zarówno w skali makroskopowej, mikroskopowej – na poziomie cząstek elementarnych, jak i w skali kosmicznej – na poziomie układów gwiezdnych i galaktyk.

Prawa zachowania a symetrie czasu i przestrzeni

Prawo zachowania momentu pędu, podobnie jak dwa pozostałe prawa zachowania występujące w mechanice, wynika z podstawowych symetrii przestrzeni i czasu. Jak już wspomniano, prawo zachowania energii wynika z symetrii czasu względem przesunięć (w czasie). Mówimy, że czas ma cechę jednorodności. Prawo zachowania pędu wynika z symetrii przestrzeni względem przesunięć. Mówimy także, że przestrzeń ma cechę jednorodności. Podobnie i prawo zachowania momentu pędu wynika z symetrii przestrzeni względem obrotów (mówiąc popularnie, pusta przestrzeń jest jednakowa w dowolnym kierunku lub – przestrzeń „wygląda tak samo”, jeżeli patrzeć w dowolnym kierunku). Mówimy, że przestrzeń jest izotropowa.

Spróbujmy w sposób uproszczony wyjaśnić, dlaczego istnieje prawo zachowania momentu pędu. Wyobraźmy sobie obracającą się w pustej przestrzeni bryłę sztywną, na którą nie działają inne ciała. Niech bryła ma pewne wybrzuszenie na jej krawędzi. Skoro bryła została raz wprowadzona w ruch obrotowy, to będzie ciągle trwała w tym stanie. Wyobraźmy sobie wektor poprowadzony od osi obrotu bryły do jej wybrzuszenia. W pewnej chwili wektor będzie wskazywał określony kierunek w przestrzeni. Ale przestrzeń jest izotropowa (jest jednakowa w dowolnym kierunku), zatem: żaden kierunek w przestrzeni nie jest w stanie zmienić jej stanu ruchu, tzn. spowolnić ją lub przyspieszyć, ponieważ każdy kierunek jest równoważny (jest „jednakowo dobry”). Po prostu nie ma powodu, dla którego bryła miałaby zmieniać swoją prędkość ruchu obrotowego.

Należy zwrócić uwagę na to, że moment pędu jest wielkością wektorową i prawo zachowania momentu pędu mówi o zachowaniu nie tylko wartości momentu pędu, ale również i o zachowaniu jego zwrotu i kierunku. Z tego wynika, że w określonych sytuacjach także oś obrotu odosobnionego układu ma stały kierunek w przestrzeni.

Przykład 9

Johannes Kepler w wyniku wieloletnich obserwacji ustalił prawa ruchu planet, zwane prawami Keplera. Przedstawiliśmy je w pierwszej klasie; będziemy je bliżej omawiać przy okazji teorii grawitacji. Każda z planet obiega Słońce po orbicie eliptycznej. W jednym z ognisk elipsy znajduje się Słońce (ściślej zdanie to powinno brzmieć: w jednym z ognisk elipsy znajduje się środek masy układu Słońce–planeta). Z prawa zachowania momentu pędu wynika, że orbitalna prędkość planety nieustannie się zmienia wraz ze zmianami jej odległości od Słońca.

Otóż drugie prawo Keplera mówi, że promień wodzący $\vec{r}$ poprowadzony ze środka Słońca do środka planety zakreśla równe pola powierzchni w równych odstępach czasu (il. 4.38). Wykażemy, że prawo to wynika z zasady zachowania momentu pędu.

Promień wodzący zakreśla równe pola powierzchni — Ilustracja 4.38. a) promień wodzący zakreśla równe pola powierzchni w równych odstępach czasu, b) powierzchnia $\Delta S$ i łuk $\Delta s$ zakreślone w czasie $\Delta t$

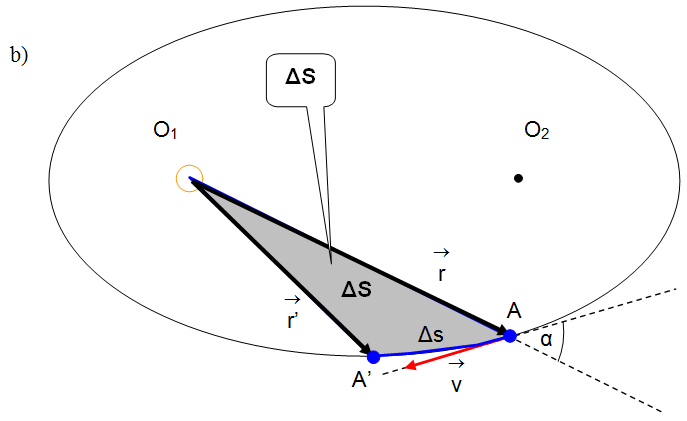
Rozwiązanie: Możemy przyjąć, że Słońce i planeta tworzą układ odosobniony. Środek masy układu Słońce–planeta pokrywa się prawie ze środkiem Słońca. Abstrahując od ruchów własnych – obrotowych – Słońca i planety, moment pędu tego układu wynosi:

L=mvr sin\alpha

( 4.61 )

gdzie $m$ – masa planety, $v$ – jej prędkość liniowa, $r$ – promień wodzący, zaś $\alpha$ – kąt między kierunkami wektorów $v$ i $r$ .

Weźmy pod uwagę mały odstęp czasu $\Delta t$ . Im jest on mniejszy, tym bardziej łuk elipsy $\Delta s$ zbliża się do odcinka $A A'$ , wycinek elipsy $O_{1}AA'$ zbliża się do trójkąta, a kąt $O_{1}AA'$ zbliża się do $\alpha$ . Uzasadnione więc jest przedstawienie pola zakreślonego przez promień wodzący w krótkim czasie $\Delta t$ jako pola trójkąta:

\Delta S=\frac{1}{2}r\Delta s sin \alpha

oraz łuku $\Delta s$ jako długości odcinka przebytego z prędkością $v$ w czasie $\Delta t$ :

\Delta s=\left|AA'\right|=r\cdot\Delta t

Oznaczmy przez $\sigma$ stosunek $\frac{\Delta s}{\Delta t}$ (czyli pole powierzchni zakreślone przez promień wodzący w jednostce czasu):

\sigma=\frac{\Delta S}{\Delta t}=\frac{1}{2}\frac{r\Delta s}{\Delta t}sin\alpha=\frac{mvr}{2m}sin\alpha=\frac{L}{2m}=const

( 4.62 )

Jest to właśnie drugie prawo Keplera wyrażone w postaci matematycznej.

Przykład 10

Kometa okrąża Słońce po orbicie eliptycznej w taki sposób, że w jednym ognisku elipsy znajduje się Słońce, zaś stosunek najdalszej do najbliższej odległości komety od Słońca wynosi $n=\frac{R_{2}}{R_{1}}=100$ . Ile razy prędkość liniowa komety jest większa, gdy się znajduje w odległości $R_{1}$ (w peryhelium), od jej prędkości liniowej w odległości $R_{2}$ (aphelium)?

Rozwiązanie: Jeśli zaniedbamy oddziaływanie komety z innymi ciałami niebieskimi i przyjmiemy, że jej masa jest stała, to stwierdzimy, że jej moment pędu jest stały i wynosi $L=mvR sin90^{o}=const$ . Wykorzystujemy fakt, że zarówno w peryhelium, jak i w aphelium kąt $\alpha$ między prędkością a promieniem wodzącym jest prosty. Zatem $mv_{1}R_{1}=mv_{2}R_{2}$ . Stąd:

\frac{v_{1}}{v_{2}}=\frac{R_{2}}{R_{1}}=100

Prędkość komety w peryhelium jest sto razy większa od jej prędkości w aphelium.

Przykład 11

Dlaczego w helikopterze stosuje się dodatkowe śmigiełko na ogonie?

Rozwiązanie: W helikopterze wielkie śmigło napędowe (nośne) uzyskuje moment pędu od silnika w kadłubie. Z prawa zachowania momentu pędu wynika, że kadłub uzyskałby taki sam moment pędu, ale przeciwnego znaku. Kadłub obracałby się w przeciwnym kierunku niż śmigło. Aby zapobiec temu niepożądanemu zjawisku, umieszcza się dodatkowe śmigło na ogonie (il. 4.40). Obraca się ono, w pionowej płaszczyźnie, w takim kierunku, aby powstał moment siły przeciwdziałający obrotowi kadłuba helikoptera.

Ilustracja 4.40. **Dodatkowe śmigło na ogonie przeciwdziała obracaniu się kadłuba helikoptera (Bell Helicopter)**

Pytania i problemy

Przytocz prawo zachowania momentu pędu. Wyjaśnij je na wybranym przykładzie.
Jaka własność przestrzeni powoduje, że obowiązuje prawo zachowania momentu pędu? Opisz tę własność.
Tancerka wykonuje piruet. Gdy ma ręce rozłożone, jej moment bezwładności wynosi $I$ , natomiast gdy złoży ręce blisko ciała, jej moment bezwładności wynosi $I^{'}$ . Stosunek momentów bezwładności $\frac{I}{I'}=\frac{5}{3}$ . Ile wynosi stosunek prędkości kątowych tancerki $\frac{\omega}{\omega'}$ ?