Transformacje Galileusza

Zasada względności Galileusza głosi, że we wszystkich układach inercjalnych dowolne zjawisko mechaniczne przebiega tak samo. Układami inercjalnymi są takie układy, w których obowiązuje pierwsza i druga zasada dynamiki. Układy inercjalne mogą się poruszać względem siebie tylko ze stałymi prędkościami.

Podamy teraz relacje matematyczne pozwalające przekształcać współrzędne jednego układu inercjalnego we współrzędne drugiego układu inercjalnego. Wyobraźmy sobie dwa układy inercjalne. Niech jeden, który nazwiemy układem $U$, ma współrzędne $x$, $y$, $z$, a drugi – $U\text{'}$ – współrzędne $x\text{'}$, $y\text{'}$, $z\text{'}$. Załóżmy, że układ $U\text{'}$ porusza się względem układu $U$ wzdłuż osi $x$ z prędkością $\overrightarrow{v}$, jak na il. 10.1. Pewien punkt $P$, który jest nieruchomy w układzie $U$, będzie się poruszał względem układu $U\text{'}$ z prędkością $-\overrightarrow{v}$. Zatem, jeżeli dla umownego czasu $t=0$ współrzędne $x$ i $x\text{'}$ są sobie równe, to w dowolnym czasie współrzędna $x\text{'}$ przybierze wartość:

Współrzędne $y$ i $z$ pozostaną niezmienione, więc:

Galileusz zakładał, że czas upływa jednakowo w obu układach, czyli:

Punkt $P$ został wybrany dowolnie, więc współrzędne każdego innego dowolnego punktu będą się transformować tak samo. Zatem układ poniższych równań wiąże wszystkie współrzędne i dowolny czas dwóch układów inercjalnych. Nosi on nazwę transformacji Galileusza:

Aż do przełomu XIX i XX wieku przyjmowano ten układ równań za poprawny, wraz z postulowaną równością czasów w obu układach. Sformułowanie teorii względności przez Einsteina pokazało jednak, że transformacje Galileusza są relacjami klasycznymi i mogą być stosowane tylko dla prędkości małych w porównaniu z prędkością światła. W ogólnym przypadku należy stosować transformacje Lorentza, o których będziemy mówić w dalszym ciągu tego rozdziału.

Prędkość światła

Przez długi czas uznawano, że prędkość światła jest nieskończenie wielka, czyli że światło pokonuje dowolną drogę momentalnie. Dopiero od około XVI wieku zaczęto podejrzewać, że światło ma skończoną prędkość. To, że prędkość światła jest skończona, pierwszy udowodnił doświadczalnie (ok. 1676 r.) Ole Roemer. Wyznaczył wtedy również jej wartość. Obserwując ruch Io – księżyca Jowisza – stwierdził, że zaćmienia tego księżyca podlegają okresowym wahaniom czasowym w zależności od tego, czy Ziemia jest po tej samej, czy po drugiej stronie względem Słońca niż Jowisz. Doszedł do wniosku, że wahania te można wyjaśnić skończoną prędkością rozchodzenia się światła. Na podstawie swych obserwacji określił prędkość światła jako równą $\mathrm{2,3}\cdot {10}^8\text{m}/\text{s}$.

Od tego czasu wykonywano wiele pomiarów prędkości światła z coraz większą dokładnością. Współczesna technika laserowa, umożliwiająca wytworzenie impulsów światła nano- i pikosekundowych, pozwala precyzyjnie określić tę prędkość. Z tych pomiarów otrzymano:

W 1983 roku wartość $c=\mathrm{2,99792458}\cdot {10}^8\text{m}/\text{s}$ została uznana za wzorzec prędkości i wraz ze wzorcem czasu (1 sekunda) pozwala zdefiniować jednostkę pochodną „1 metr” (jako odległość, jaką światło przebywa w próżni w czasie 1/299792458 sekundy). Wraz z tą decyzją Generalnej Konferencji Miar i Wag zakończyła się era pomiarów prędkości światła, wyrażania jej za pomocą jednostek podstawowych (1 m i 1 s) i określania niepewności pomiarowej wyniku. Dziś wartość $c$ znana jest dokładnie.

W drugiej połowie XIX wieku, wraz z rozwojem elektrodynamiki powstało pytanie, względem jakiego układu odniesienia prędkość ta jest mierzona. Przez analogię do dźwięku rozchodzącego się w powietrzu przyjęto, że światło rozchodzi się w niewidzialnym ośrodku, tzw. eterze. Eter musiałby zatem wypełniać całą przestrzeń kosmiczną. Przyjęto, że prędkość światła otrzymana z pomiarów jest mierzona względem eteru i że jest ona równa $c$ tylko w takim układzie, który spoczywa względem eteru. Dla obserwatora, który zbliżałby się do źródła światła z prędkością $v$, prędkość światła wynosiłaby $c+v$.

Albert Michelson (urodzony w Polsce, w Strzelnie – małym mieście na Kujawach) w roku 1887 wykonał doświadczenie, za pomocą którego wykazał, że światło porusza się ze stałą prędkością $c$, niezależnie od prędkości źródła lub obserwatora. Później wielu uczonych (w tym Edward Morley we współpracy z Michelsonem) wykonywało podobne doświadczenia z coraz większą dokładnością i zawsze uzyskiwało taki sam wynik, świadczący o stałości prędkości światła.

Stałości prędkości światła nie potrafiono wytłumaczyć na gruncie transformacji Galileusza. Powstała konieczność rewizji idei, które były podstawą tej teorii. Zadanie to rozwiązał Einstein, który odrzucił pojęcie eteru, oparł się na zasadzie względności i odkrył zupełnie nowe własności przestrzeni i czasu.

Postulaty Einsteina

Einstein zbudował teorię względności, opierając się na dwóch postulatach. Pierwszy z nich to zasada względności, której treść jest następująca:

Treścią drugiego postulatu jest zasada niezmienności prędkości światła:

Zasada względności Einsteina jest ogólniejsza od zasady względności Galileusza. Galileusz zakładał (tylko) jednakowy przebieg zjawisk mechanicznych w różnych układach inercjalnych. Nie mogło być inaczej, gdyż za jego czasów niewiele wiedziano o elektryczności i magnetyzmie, niczego nie wiedziano o falach elektromagnetycznych, a takie określenia, jak „ruch” i „prędkość” odnosiły się właśnie do zjawisk mechanicznych. Einstein przyjął, że dowolne zjawiska (nie tylko mechaniczne), przebiegają jednakowo w różnych układach inercjalnych. Ruch światła jest jednym z takich „niemechanicznych” zjawisk.

Na przełomie XIX i XX wieku było jasne, że równania Maxwella nie są zgodne z transformacją Galileusza. Wiedziano w szczególności, że prędkość fali elektromagnetycznej (prędkość światła) nie może wynosić zero w żadnym układzie odniesienia. Z kolei transformacja Galileusza przewidywała istnienie takiego układu odniesienia. Fizycy w owym czasie (m. in. Hendrik Lorentz, laureat Nagrody Nobla w 1902 r., wyprowadził tzw. transformacje Lorentza, będące uogólnieniem transformacji Galileusza) próbowali, bez powodzenia, usunąć tę sprzeczność. Nie kwestionowali oni bowiem ani transformacji Galileusza (ta doskonale sprawdzała się w praktyce zjawisk „mechanicznych”), ani równań Maxwella (te doskonale opisywały zjawiska elektromagnetyczne). Einstein poszedł inną drogą: transformację Galileusza odrzucił (dokładniej: uznał ją za przybliżoną), a wnioski wynikające z równań Maxwella, poparte wynikami doświadczeń, uznał za poprawne.

Wydarzenia i czasoprzestrzeń

W szczególnej teorii względności operujemy pojęciem wydarzenia, nadając mu nieco inny sens, niż w mowie potocznej. Wydarzenie to para, na którą składa się pewne położenie w przestrzeni, opisane współrzędnymi [x; y; z] w jakimś układzie odniesienia, wyposażonym w układ współrzędnych i pewien czas $t$ (mierzony czy odliczany w tymże układzie odniesienia). Tak więc wydarzenie możemy zapisać jako {[x; y; z]; t}. Zamiennie używa się także nazwy zdarzenie.

Zbiór wydarzeń tworzy czterowymiarową czasoprzestrzeń. Można więc przyjąć – wyłącznie dla celów poglądowych – określenie „punkto-chwila” dla scharakteryzowania istoty wydarzenia. By podkreślić niejaką „jedność” czasu i przestrzeni, wydarzenie zapisuje się jako [x; y; z; t] albo wręcz w postaci [x; y; z; ct], w której wszystkie cztery współrzędne są wyrażone w tych samych jednostkach – w metrach. Bardzo często, omawiając proste zagadnienia, operujemy dla większej poglądowości dwuwymiarową czasoprzestrzenią [x; t].

Dylatacja czasu

Z postulatów teorii względności można wyprowadzić tezę, że czas jest względny. Istotę tego efektu można wyrazić następująco: Czas trwania jakiegoś zjawiska zachodzącego w pewnym punkcie jest najkrótszy w układzie, względem którego punkt ten spoczywa.

To samo możemy ująć w języku wydarzeń: jeśli mamy dwa wydarzenia $A$ i $B$ (odpowiadają one, odpowiednio, początkowi i końcowi zjawiska), to różnica $\Delta t_{AB}=t_B-t_A$ (czyli czas trwania zjawiska) nie jest jednakowa we wszystkich układach odniesienia. Jest ona najmniejsza w takim układzie odniesienia, w którym $\Delta x_{AB}=x_B-x_A=0$ i $\Delta y_{AB}=y_B-y_A=0$ i $\Delta z_{AB}=z_B-z_A=0$ (czyli początek i koniec zjawiska następują w tym samym punkcie).

Zależność między czasem $t$ trwania zjawiska zachodzącego w układzie poruszającym się względem układu odniesienia, mierzonym w układzie nieruchomym, a czasem $t_0$ trwania tego samego zjawiska, ale mierzonym w poruszającym się układzie, wyrażamy za pomocą wzoru:

Mianownik w tym wzorze jest mniejszy od jedności, więc $t>t_0$, czyli według obserwatora nieruchomego czas trwania zjawiska zachodzącego w układzie poruszającym się względem niego jest dłuższy niż czas trwania tego samego zjawiska, ale odbywającego się w układzie ruchomym. Czas $t_0$ nazywa się czasem własnym. Jest to czas trwania zjawiska mierzony w pewnym punkcie spoczywającym względem obserwatora. Relatywistyczny efekt wydłużenia czasu został potwierdzony doświadczalnie.

Z teorii względności wynika bardzo ciekawy efekt, zwany „paradoksem bliźniąt”, który może wystąpić przy prędkościach bliskich prędkości światła. Dzięki temu efektowi można by „podróżować w przyszłość”. Kosmonauci podróżujący z prędkością bliską prędkości światła po powrocie na Ziemię stwierdziliby, że na Ziemi upłynął dużo dłuższy czas niż w ich życiu – mogliby się znaleźć nawet w następnym stuleciu, podczas gdy ich rówieśnicy dawno by poumierali.

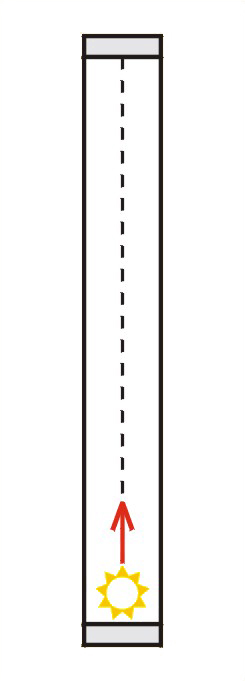
Pokażemy teraz, jak z prostego zastosowania postulatów teorii względności wynika, że czas upływa niejednakowo w różnych układach. Zasadę niezmienniczości prędkości światła oraz zasadę względności zastosujemy do pomiaru czasu za pomocą prostego zegara zwanego „zegarem świetlnym”. Zegarem takim może być rura o ustalonej długości $d$ zamknięta dwoma równoległymi zwierciadłami doskonale odbijającymi światło, do której wpuszczono krótki impuls świetlny przebiegający ją w jedną i drugą stronę (il. 10.4). Odcinki czasu, w którym światło przebiega rurę, są jednakowe, czyli takie urządzenie można uznać za zegar.

Będziemy teraz za pomocą takich zegarów porównywać przebieg czasu upływającego w dwóch układach – w „nieruchomym” $U$ i „ruchomym” $U\text{'}$. Zgodnie z tym, co powiedzieliśmy wcześniej, pomiaru czasów dla poszczególnych zdarzeń możemy dokonywać tylko na zegarach znajdujących się w bezpośrednim sąsiedztwie tych zdarzeń. Nie można zatem porównywać czasu jednego zegara spoczywającego w układzie $U$ z jednym zegarem ruchomym, ponieważ kolejne wskazania czasu zegara ruchomego odbywają się w różnych miejscach w układzie $U$. Dla porównania czasów w obu układach należy w układzie $U$ rozmieścić wiele zsynchronizowanych ze sobą zegarów, które będzie mijał zegar ruchomy, spoczywający jednak w układzie $U\text{'}$.

Na il. 10.5 przedstawiono interesującą nas sytuację. W miejscach oznaczonych $1$– $5$ rozmieszczono identyczne zegary. W każdym z tych miejsc impuls świetlny bądź to startuje od lustra dolnego (miejsca $1$, $3$ i $5$), bądź zawraca przy lustrze górnym (miejsca $2$ i $4$). Czas przebiegu światła w jedną stronę w zegarze nieruchomym wynosi $t_0=\frac{d}{c}$. Takie odcinki czasu odmierzają kolejno zegary rozmieszczone w punktach $1$ do $5$. Czas przebiegu światła w identycznym zegarze ruchomym mierzony w układzie $U\text{'}$ jest dokładnie taki sam, ponieważ zegar w tym układzie spoczywa i światło ma do przebycia taką samą drogę $d$, z taką samą prędkością, która tu również wynosi $c$. Natomiast obserwator nieruchomy w układzie $U$ widzi, że światło biegnące w zegarze ruchomym przebywa drogę po przekątnej, czyli dłuższą (il. 10.5b) i musi zużyć więcej czasu na dotarcie do górnego zwierciadła. Na rysunku przedstawiona jest sytuacja, w której droga $s$ jest dwukrotnie większa od $d$ (gdy kąt $\alpha =30°$, wówczas $s=\frac{d}{sin\alpha }=2d$). W tym przypadku zdarzenie $2$ – dotarcie sygnału do górnego lustra w zegarze nieruchomym – występuje wtedy, gdy światło w zegarze ruchomym znajduje się w połowie drogi od dolnego do górnego zwierciadła. Światło w zegarze ruchomym dociera do górnego zwierciadła dopiero w miejscu oznaczonym $3$. Widzimy, że zegar ruchomy spóźnia się w stosunku do mijanych kolejno zegarów nieruchomych. To opóźnienie nazywamy spowolnieniem czasu lub dylatacją czasu.

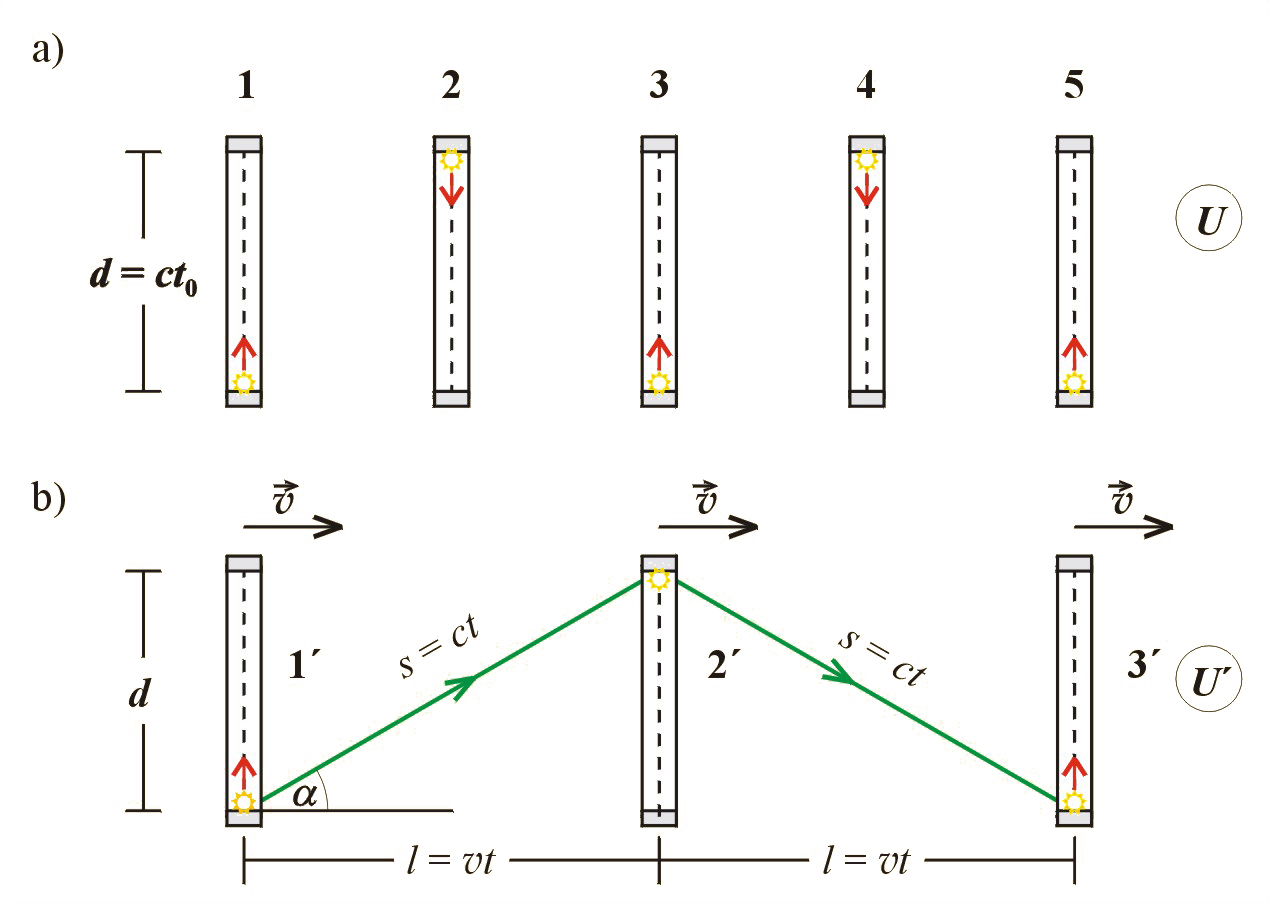
Jesteśmy teraz w stanie obliczyć, ile wynosi dylatacja zegara mierzącego czas w układzie $U\text{'}$ poruszającym się z dowolną stałą prędkością $\overrightarrow{v}$ względem układu $U$. Wystarczy obliczyć, o ile spóźni się zegar poruszający się z dowolną stałą prędkością $\overrightarrow{v}$. Czas przelotu światła po drodze $s$ oznaczymy przez $t$, zatem:

Z drugiej strony, stosując twierdzenie Pitagorasa, mamy, że $s^2=d^2+l^2$, gdzie $l$ jest drogą, jaką przebywa zegar ze stałą prędkością $\overrightarrow{v}$ w czasie $t$; $l=vt$, a $d=c{t}_0$, zatem:

lub

Stąd wzór wcześniej podany:

Na przykładzie zegarów świetlnych można w dość prosty sposób wytłumaczyć, na czym polega „paradoks bliźniąt”. Najpierw zauważmy, że dylatacja czasu dana za pomocą wzoru (10.6) jest względna. To znaczy, że taki sam efekt spowolnienia czasu występuje z punktu widzenia zarówno jednego, jak i drugiego układu inercjalnego. Wynika to stąd, że sytuacja układu $U\text{'}$ jest symetryczna względem układu $U$. Układ $U\text{'}$ porusza się z prędkością $\overrightarrow{v}$ względem układu $U$, ale i układ $U$ porusza się z taką samą prędkością $\overrightarrow{v}$ (lecz przeciwnie zwróconą) względem układu $U\text{'}$. Zatem, gdybyśmy chcieli porównywać wskazania jednego zegara spoczywającego w układzie $U$ z mijanymi zegarami układu $U\text{'}$, to obserwator znajdujący się w układzie $U$ stwierdziłby, że jego zegar spóźnia się wobec tych zegarów. I nie ma tu żadnej sprzeczności, gdyż w obydwu przypadkach zachodzi porównanie czasu jednego zegara z każdym mijanym zegarem innego układu inercjalnego. Czas własny w obu układach jest jednakowy.

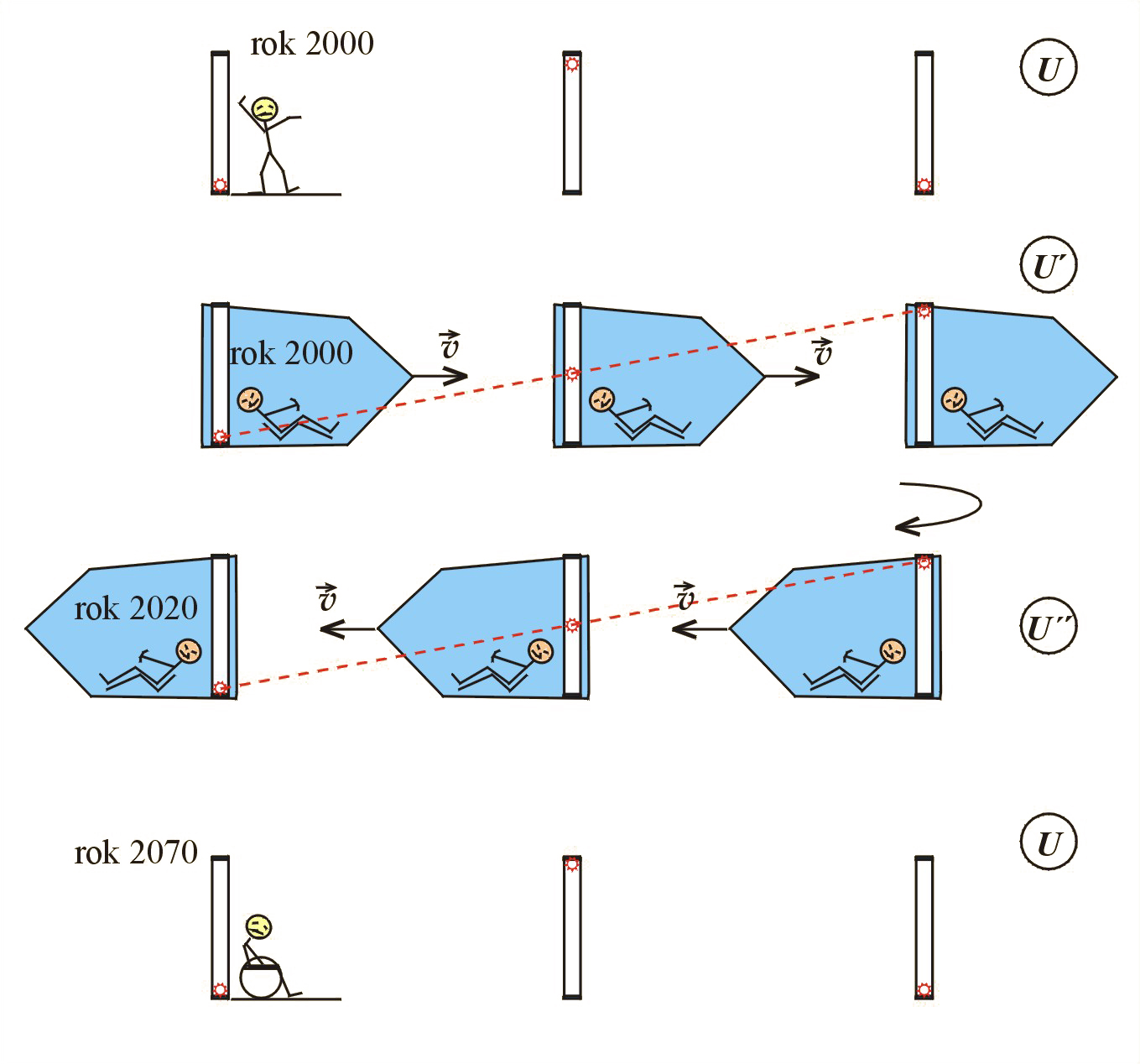
Wydawać by się mogło, że nie ma możliwości stwierdzenia różnego upływu czasu w różnych układach inercjalnych. Jednakże taka możliwość pojawi się, jeżeli jeden z układów zmieni zwrot swojej prędkości na przeciwny (choć w czasie zawracania nie jest inercjalny). Wtedy na zegarach obu układów można porównać upływ czasu. W opisanej sytuacji oba układy nie mają jednakowej historii, gdyż jeden z nich zmieniał swoją prędkość, a drugi nie. W efekcie końcowym, czas powinien płynąć wolniej w układzie, który zawracał. Zobrazowane jest to na il. 10.6. Jeden bliźniak pozostaje w układzie $U$ na Ziemi, drugi bliźniak – kosmonauta – mija kolejne zegary układu $U$ i stwierdza, że jego zegar spóźnia się w stosunku do mijanych. Na tym etapie ruchu oba układy $U$ i $U\text{'}$ są w symetrycznej sytuacji. Sytuacja zmienia się, gdy kosmonauta zawróci (musi najpierw wyhamować, a następnie przyspieszyć, ale w przeciwną stronę). Powracający kosmonauta jak gdyby przesiadł się do nowego układu $U\text{'}\text{'}$. Po powrocie na Ziemię ma możliwość porównania czasu, który upłynął na jego zegarze w rakiecie, z czasem na zegarze brata bliźniaka. Stwierdzi, że brat postarzał się dużo bardziej niż on.

Transformacje Lorentza

W trakcie dotychczasowych naszych rozważań dowiedzieliśmy się, że transformacje Galileusza nie są zgodne z zasadą stałości prędkości światła oraz nie uwzględniają względności czasu. Transformacje te są słuszne tylko dla prędkości małych w porównaniu z prędkością światła. Widzimy zatem, że w teorii względności muszą obowiązywać inne transformacje współrzędnych czasoprzestrzennych wydarzeń przy przejściu z jednego do drugiego układu inercjalnego. Właściwe transformacje obowiązujące w teorii względności noszą nazwę transformacji Lorentza.

Transformacje Lorentza (dla układów przedstawionych na il. 10.1):

Widzimy, że transformacje Lorentza różnią się wyraźnie od transformacji klasycznych Galileusza (10.4). W transformacjach klasycznych przestrzeń i czas są wielkościami wzajemnie niezależnymi. W transformacjach Lorentza mamy ścisły związek między współrzędnymi przestrzennymi i czasowymi. Nie tylko współrzędne przestrzenne zależą od czasu (występowało to również w transformacjach Galileusza), ale i czas zależy od współrzędnych przestrzennych – to właśnie jest odzwierciedleniem wzajemnego powiązania przestrzeni i czasu w teorii względności. W przekształceniach Galileusza czas jest absolutem niezależnym od układu odniesienia, dlatego w transformacji czasu nie mają udziału współrzędne przestrzenne.

Względność wymiarów przestrzennych

Prostą konsekwencją transformacji Lorentza jest względność wymiarów przestrzennych mierzonych w różnych układach odniesienia. Aby się o tym przekonać, przeprowadzimy następujące rozumowanie: Przypuśćmy, że obserwator w układzie $U$ postanowił zmierzyć długość ruchomego względem niego pręta.

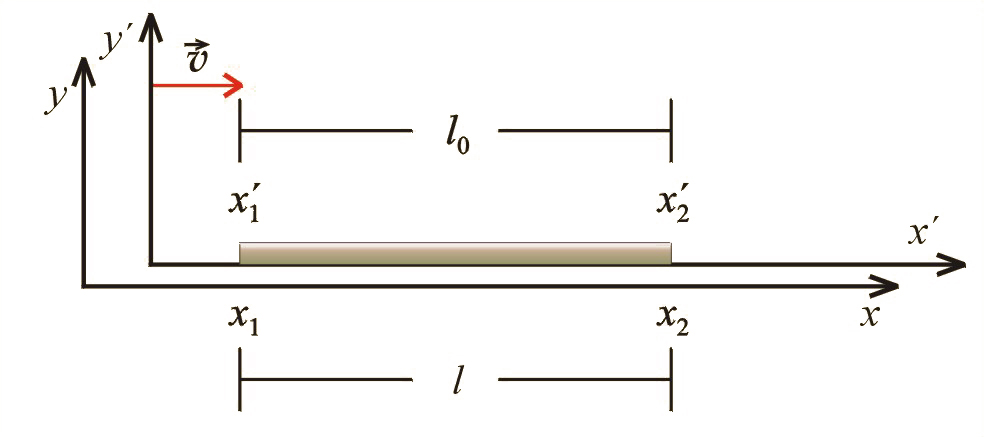
Niech pręt spoczywa w układzie $U\text{'}$, a jego końce znajdują się w punktach $x_1^{\text{'}}$ i $x_2^{\text{'}}$ (il. 10.7). Długość pręta mierzoną w układzie $U\text{'}$ oznaczymy przez $l_0$, więc:

Dla obserwatora w układzie $U$ pręt porusza się z prędkością $\overrightarrow{v}$. Obserwator ten, w celu zmierzenia długości pręta, musi wyznaczyć współrzędne $x_1$ i $x_2$ obu końców pręta, ale współrzędne te podczas ruchu pręta ciągle się zmieniają. Aby uzyskać właściwy wynik, należy zmierzyć jednocześnie (w określonej chwili $t$) współrzędne chwilowego położenia końców pręta. Dla tego obserwatora długość pręta wyniesie:

Z transformacji Lorentza (10.6) mamy:

Po odjęciu tych równań stronami otrzymamy:

więc zgodnie z (10.8) i (10.9):

Otrzymaliśmy znany wzór na tzw. skrócenie Lorentza.

Czterowymiarowa czasoprzestrzeń Minkowskiego

Jednym z najbardziej pasjonujących aspektów fizyki jest jej zdolność do pokonywania bariery wyobraźni. Przykładem tego jest teoria względności. Wyobraźnia człowieka nie sięga poza przestrzeń o trzech wymiarach. Potrafimy wyobrazić sobie przestrzenie o mniejszej liczbie wymiarów – przestrzeń dwuwymiarową jako powierzchnię (mającą tylko dwa wymiary: szerokość i długość, brak jej trzeciego wymiaru – grubości) oraz przestrzeń jednowymiarową jako linię (mającą jedynie jeden wymiar – długość). Hermann Minkowski, opierając się na szczególnej teorii względności Einsteina, wprowadził do fizyki pojęcie przestrzeni czterowymiarowej.

W teorii względności czas i przestrzeń są wzajemnie powiązane. Przekształcenie czasu zależy od miejsca, w jakim to przekształcenie następuje, a przekształcenie współrzędnych przestrzennych – od czasu. Minkowski wypowiada się w tej sprawie następująco: Odtąd przestrzeń i czas rozpatrywane oddzielnie stają się pojęciami skazanymi na odrzucenie, natomiast połączenie tych dwóch pojęć przetrwa jako obiektywna rzeczywistość.

Dlatego teoria względności zamiast do przestrzeni oraz czasu odwołuje się do jednolitej czterowymiarowej czasoprzestrzeni. Ta czterowymiarowa przestrzeń jest uogólnieniem zwykłej trójwymiarowej przestrzeni $x$, $y$, $z$. Uogólnienie polega na tym, że do trzech wzajemnie prostopadłych osi $x$, $y$ i $z$ dodaje się jeszcze czwartą oś związaną z czasem jako $x_4=ct$, której, oczywiście, nie można umieścić w przestrzeni trójwymiarowej, lecz poza nią, jako oś prostopadłą do trzech pozostałych. I tego właśnie nie potrafimy sobie wyobrazić; potrafimy sobie wyobrazić dwie linie prostopadłe na płaszczyźnie, również i trzy linie wzajemnie prostopadłe w zwykłej przestrzeni, natomiast cztery linie wzajemnie prostopadłe wykraczają poza naszą wyobraźnię.

W tej czterowymiarowej przestrzeni (zwanej też czasoprzestrzenią) będziemy się posługiwać następującymi oznaczeniami poszczególnych współrzędnych (zwykle dla czasoprzestrzeni rzeczywistej stosuje się trochę inne oznaczenia współrzędnych – tu świadomie zastosowaliśmy oznaczenia prostsze):

Poszczególne punkty w tej przestrzeni określone są przez cztery współrzędne: trzy przestrzenne i jedną czasową. Punkty te nazywamy zdarzeniami.

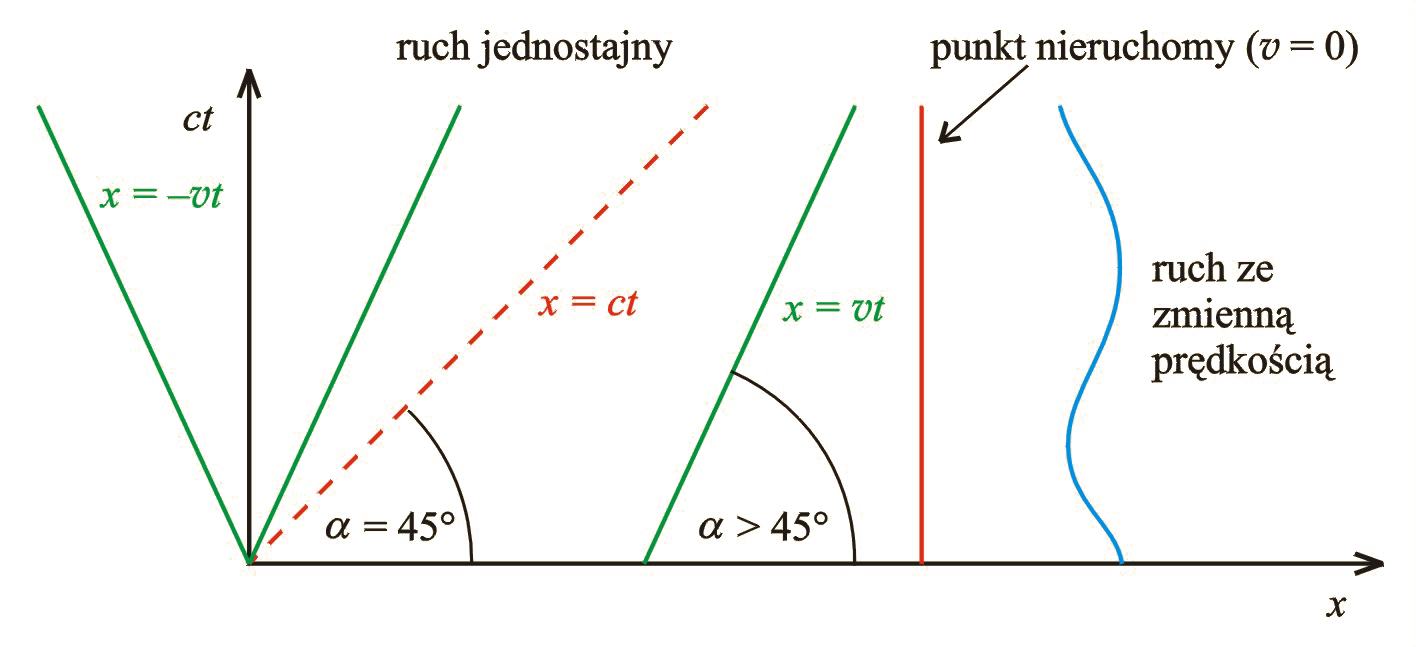
Mimo że czterowymiarowa czasoprzestrzeń jest niewyobrażalna, jednak można wyobrazić sobie przekroje czasoprzestrzeni płaszczyznami wyznaczonymi przez proste $\text{(}{x}_1$ i $x_4\text{)}$, $\text{(}{x}_2$ i $x_4\text{)}$, $\text{(}{x}_3$ i $x_4\text{)}$. Jeden z takich przekrojów czasoprzestrzeni płaszczyzną wyznaczoną przez proste $x$ i $ct$ (czyli przez $x_1$ i $x_4$) przedstawiony jest na il. 10.8. Otrzymujemy w ten sposób wykres czasoprzestrzenny. Linie przedstawione na wykresie czasoprzestrzennym nazywamy liniami świata. Spoczywający punkt jest reprezentowany przez linię prostą równoległą do osi czasowej. Punkt poruszający się ruchem jednostajnym jest reprezentowany przez linię prostą nachyloną do osi $x$ pod kątem większym od $45°$. Linia prosta nachylona pod kątem $45°$ oznacza ruch z prędkością światła $c$. Zatem linia wyobrażająca ruch z dowolną prędkością ciała o masie większej od zera musi być wszędzie nachylona do osi $x$ pod kątem większym od $45°$, ponieważ $c$ jest prędkością maksymalną.

W czasoprzestrzeni, podobnie jak w zwykłej przestrzeni, występują również wektory, zwane czterowektorami, gdyż mają cztery rzuty na cztery osie współrzędnych. Odpowiednikiem wektora położenia o składowych $x$, $y$, $z$ jest czterowektor o składowych $x$, $y$, $z$, $ct$. Innym podstawowym czterowektorem jest czteropęd. Łączy on trójwymiarowy wektor pędu z energią kinetyczną, która jest wielkością skalarną.

Dynamika relatywistyczna

Dotychczas zajmowaliśmy się własnościami przestrzeni i czasu. Teraz omówimy relatywistyczne ujęcie takich wielkości, jak siła, pęd i energia. Zobaczymy, że podstawowe zasady zachowania pędu i energii w teorii względności obowiązują nadal, ale nabierają nowego sensu. Pojawi się nowy wzór, który nie był znany w teorii klasycznej – słynny wzór Einsteina na równoważność masy i energii $E=m{c}^2$. Nasze rozważania zaczniemy od omówienia pędu relatywistycznego.

Pęd relatywistyczny

Wiemy, że fizyka relatywistyczna, zamiast zwykłymi wektorami o trzech współrzędnych, posługuje się czterowektorami mającymi trzy współrzędne przestrzenne i czwartą – czasową. Podobnie jest z pędem. Czteropęd cząstki o masie $m$ i prędkości $\overrightarrow{v}=\left(v_x;v_y;v_z\right)$ definiujemy za pomocą jego czterech składowych, które mają postać:

Trzy składowe przestrzenne czteropędu – $p_1$, $p_2$, $p_3$ – są jednocześnie współrzędnymi wektora pędu relatywistycznego.

Zatem pęd relatywistyczny ma postać:

Podlega on prawu zachowania.

Energia

Szczególnie ciekawa jest interpretacja czwartej składowej czteropędu $p_4$ – jest to po prostu energia dzielona przez stałą $c$ $\text{(}{p}_4=\frac{E}{c}\text{)}$. Korzystając zatem ze wzoru (10.25), otrzymujemy wzór na energię relatywistyczną ciała poruszającego się z prędkością $\overrightarrow{v}$:

Widzimy tu piękne połączenie tego, co w mechanice klasycznej występowało oddzielnie. Pęd i energia są powiązane we wspólnym czterowymiarowym wektorze jako jego rzuty na osie przestrzenne i na oś czasową. W miejsce dwóch niezależnych praw zachowania pędu i energii mamy jedno wspólne prawo zachowania czterowektora pędu.

Energia spoczynkowa

Patrząc na wzór (10.27), nie widzimy podobieństwa do klasycznego wzoru na energię kinetyczną:

Czyżby wzór relatywistyczny na energię nie zgadzał się ze wzorem klasycznym dla małych prędkości? Żeby rozstrzygnąć tę kwestię, zapiszmy wzór (10.27) w postaci:

oraz zastosujmy przybliżony wzór na występujący tu dwumian:

Otrzymamy wtedy:

Zatem nowa definicja energii zgadza się z klasyczną, jeżeli do wzoru klasycznego dodamy stałą wielkość:

Wyraz ten nie znika nawet wtedy, gdy prędkość ciała jest równa zeru. Oznacza on energię spoczynkową ciała. Jest to słynny wzór Einsteina na równoważność masy i energii, który oznacza, że każde ciało ma energię spoczynkową określoną przez jego masę pomnożoną przez czynnik $c^2$ (nie należy mylić tej energii spoczynkowej z energią potencjalną ciała w polu sił zewnętrznych). Wzór ten wyraża bardzo ważną rzecz, nieznaną w teorii klasycznej, że energia spoczynkowa – wewnętrzna – ciała (lub dowolnego układu zamkniętego ciał) jest równoważna jego masie. Zatem bezwładność ciała jest miarą jego energii. Każda zmiana energii $\Delta E_0$ pociąga za sobą zmianę $\Delta m$ masy ciała.

Wzór ten ma doniosłe znaczenie zarówno poznawcze, jak i praktyczne. Dzięki niemu możemy głębiej zrozumieć pojęcie masy. Konsekwencje praktyczne to energia jądrowa wyzwalana w reakcjach rozpadu jąder uranu w elektrowniach jądrowych i bombach nuklearnych oraz energia reakcji syntezy jąder wyzwalana w bombach wodorowych. Głównym źródłem energii gwiazd i naszego Słońca są właśnie reakcje syntezy jądrowej.

Siła

W fizyce relatywistycznej ulegają modyfikacji nie tylko wyrażenia na pęd i energię, ale również i podstawowe prawo dynamiki – druga zasada dynamiki Newtona. Prawidłowy wzór relatywistyczny na siłę otrzymamy, gdy do wzoru Newtona (tom II, rozdział 2.5. Pęd i popęd, wzór (10.31)) w postaci:

podstawimy relatywistyczny wzór na pęd (10.26) przy założeniu, że $\Delta t$ jest małe.

Zasada korespondencji

Przyglądając się wzorom relatywistycznym, widzimy, że różnią się one od wzorów klasycznych. Powstaje wobec tego pytanie: Czy nowe prawa relatywistyczne unieważniają dotychczasowe klasyczne? Tak nie jest, gdyż dla prędkości małych w porównaniu z prędkością światła wzory relatywistyczne przechodzą w klasyczne. Widzieliśmy to wyraźnie, rozpatrując wzór na energię kinetyczną. To samo widać we wzorze (10.26) na pęd. Ogólna zasada jest taka, że wzory relatywistyczne przechodzą we wzory klasyczne wtedy, gdy $\frac{v^2}{c^2}\ll 1$.

Zatem „stare” prawa klasyczne stanowią przybliżenie „nowych” praw relatywistycznych. „Stare” prawa klasyczne nie tracą swojej wartości, są nadal prawdziwe dla prędkości małych w porównaniu z prędkością światła. Prawa relatywistyczne stosują się do całego zakresu prędkości. Teoria relatywistyczna nie obala więc teorii klasycznej, ale ogranicza zakres jej ważności.

Powyższe stwierdzenie jest przykładem działania tak zwanej zasady korespondencji lub zasady odpowiedniości. Zasada ta głosi, że zarówno w fizyce, jak i w innych naukach ścisłych, sprawdzone doświadczalnie prawa nie muszą być obalane przez nowe teorie. Często zdarza się, że nowa teoria ustanawia zakres ważności starej teorii, przez ustanowienie nowych praw rozszerza ten zakres i rzuca w ten sposób światło na szerszy krąg zagadnień. Ponadto nowa teoria zawiera w sobie starą teorię jako jej przybliżenie.

Zasada korespondencji ukazuje jeden z bardzo istotnych elementów rozwoju nauki. Najpierw powstaje teoria na podstawie opisu wyników wcześniejszych doświadczeń. W miarę jak gromadzą się nowe doświadczenia, doskonali się technika pomiarowa, pomiary stają się coraz dokładniejsze oraz powstają nowe odkrycia, istniejąca teoria radzi sobie z nimi coraz gorzej. Powstaje konieczność opracowania nowej teorii obejmującej wszystkie znane zjawiska. Nowa teoria na ogół nie obala starej, która została sprawdzona na pewnym wcześniej uzyskanym materiale doświadczalnym. Nowa teoria wyjaśnia zarówno stare, jak i nowo odkryte zjawiska. Dlatego jest ona ogólniejsza od starej teorii, gdyż zawiera starą teorię w sobie, jako graniczny przypadek.

Nowa teoria musi się oprzeć na nowych założeniach, często rewolucyjnych w stosunku do starej teorii. Stara teoria zostaje poddana ostrej krytyce. Wywiązuje się ostra walka między zwolennikami starej i nowej teorii. Nowa teoria musi przezwyciężyć poglądy, które traktowane są jako „oczywiste” i „same przez się zrozumiałe” – dlatego prawdziwe. Obrońcy starej teorii zwykle zarzucają nowej, że kłóci się ze zdrowym rozsądkiem. Jednak okazuje się, że tak zwany zdrowy rozsądek wynika po prostu z naszych przyzwyczajeń. W końcu prędzej czy później zwycięża nowa teoria, szczególnie wtedy, gdy kolejne doświadczenia ją potwierdzają. Następne pokolenia nie mogą zrozumieć, dlaczego przy powstawaniu nowych teorii toczyły się tak burzliwe i dziwne dyskusje.