5.2. Wahadło

W tym rozdziale opiszemy ruch wahadła. Zobaczymy, że im krótsze wahadło, tym szybciej się waha – ma krótszy okres wahań.

Wahadło matematyczne

Wahadło matematyczne jest to ciężarek o małych rozmiarach zawieszony na cienkiej nici, który może się wahać (il. 5.6). Zatem do rozważań nad jego ruchem możemy przyjąć, że wahadło matematyczne to układ składający się z punktu materialnego umieszczonego na nierozciągliwej i nieważkiej nici o długości $l$ .

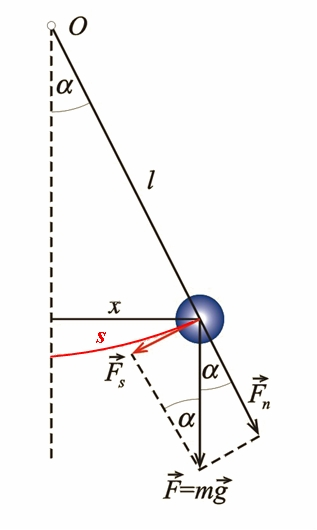
Ciężarek porusza się po łuku okręgu, więc miarą jego wychylenia z położenia równowagi jest długość łuku $s$ . Składowa siły ciężkości $\vec{F}_{s}$ jest skierowana wzdłuż tego łuku. Rozważymy ruch wahadła w tzw. przybliżeniu małych drgań, dla których kąt wychylenia $\alpha$ nie przekracza kilku stopni (il. 5.6). W tym przybliżeniu przyjmujemy, że wychylenie punktu liczone po łuku $s$ (czerwona linia na il. 5.6) jest równe długości $x$ poziomego odcinka. Wyraźnie widać, że przybliżenie to jest tym lepsze, im kąt wychylenia $\alpha$ jest mniejszy. Możemy zatem wyrazić $\{F}_{s}$ :

F_{s}=mg\sin\alpha=mg\frac{x}{l}

Widzimy, że siła ta jest proporcjonalna do wychylenia $s$ . Jest ona zwrócona zawsze do środka, tzn. zawsze ma znak przeciwny do znaku wychylenia $s$ . Uwzględniając tę właściwość, możemy napisać, że:

F_{s}=-\frac{mg}{l}s

Siła ta ma postać siły kwazisprężystej (5.13): $F=-kx$ , gdzie:

k=\frac{mg}{l}

a rolę wychylenia $x$ pełni długość łuku $s$ .

Jak stwierdziliśmy w poprzednim podrozdziale, jeżeli na układ działa siła kwazisprężysta, to układ ten może wykonywać drgania harmoniczne. Tak jest w naszym przypadku, więc wahadło matematyczne wykonuje drgania harmoniczne o okresie drgań (zgodnie ze wzorem (5.16)):

T=2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{m}{\frac{mg}{l}}}

Po prostym przekształceniu otrzymujemy wzór na okres drgań wahadła matematycznego:

T=2\pi\sqrt{\frac{l}{g}}

( 5.17 )

Widzimy, że nie zależy on od masy wahadła ani od amplitudy drgań (przy małych wychyleniach).

Wzór (5.17) może służyć do doświadczalnego wyznaczenia przyśpieszenia ziemskiego $g$ , gdy znana jest długość $l$ wahadła i jego okres drgań $T$ . Po przekształceniu tego wzoru otrzymujemy:

g=4\pi^{2}\frac{l}{T^{2}}

( 5.18 )

Wzorem tym się posłużymy, wykonując doświadczenie „Wahadło”.

Przykład 3

„Wahadło sekundowe” to takie, którego okres wynosi $T=1\, s$ . Oblicz, jaką długość $l$ powinno mieć wahadło matematyczne, aby było wahadłem sekundowym.

Rozwiązanie: Po przekształceniu wzoru (5.18) otrzymujemy:

l=\frac{gT^{2}}{4\pi^{2}}

więc

l=\frac{9,81\,\frac{m}{s^{2}}\cdot\left(1\, s\right)^{2}}{4\cdot\left(3,14\right)^{2}}=0,248\, m=25\, cm

Oznacza to, że aby okres wahadła wynosił 1 s, powinno ono mieć długość około 25 cm.

W rzeczywistości wahadło matematyczne możemy wykonać tylko w przybliżeniu. Głównie dlatego, że nie możemy zredukować wymiarów ciężarka do punktu materialnego. Rzeczywiste wahadło to tzw. wahadło fizyczne.

Wahadło fizyczne

Wahadłem fizycznym nazywamy dowolną bryłę sztywną, która może wykonywać drgania w jednej płaszczyźnie względem osi zawieszenia. Wahadło fizyczne przedstawiono na il. 5.7. Symbol $O$ oznacza oś zawieszenia wahadła, $S$ – jego środek masy, $l$ – odległość środka masy $S$ od osi zawieszenia $O$ . Odchylając wahadło o mały kąt $\alpha$ , spowodujemy, że będzie wykonywało drgania harmoniczne.

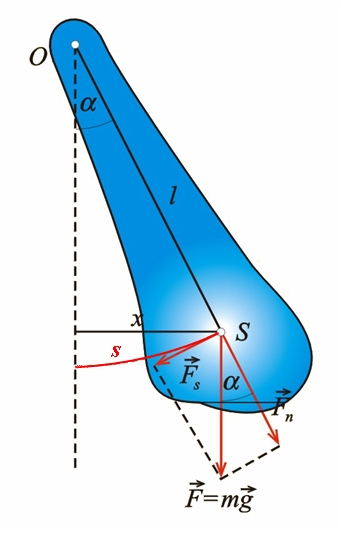
Aby wyprowadzić wzór na okres wahań wahadła fizycznego, zwrócimy uwagę na analogię między ruchem bryły sztywnej i ruchem punktu materialnego. Wykorzystamy także wyniki rozważań z rozdziału 5.1. Oscylator harmoniczny. Odpowiednikiem równania (5.12):

F=ma=-m\omega^{2}x

jest dla wahadła fizycznego (bryły sztywnej, patrz tom. II, rozdział 4.6 Moment pędu i druga zasada dynamiki dla bryły sztywnej) równanie:

M=I\varepsilon=-I\omega^{2}\alpha

(wykorzystaliśmy tu wzór $M=I\varepsilon$ , podstawową zasadę dynamiki bryły sztywnej – patrz tom II, wzór (4.55), oraz analogie: $m\leftrightarrow I$ , $x\leftrightarrow\alpha$ ). Odpowiednikiem równania (5.13):

F=-kx

jest dla wahadła fizycznego równanie:

M=-K\alpha

( 5.19 )

(wykorzystaliśmy tu analogie: $F\leftrightarrow M$ , $x\leftrightarrow\alpha$ ). Po porównaniu prawych stron powyższych wzorów na $M$ , otrzymamy:

K=I\omega^{2}

Stąd

\omega=\sqrt{\frac{K}{I}}

( 5.20 )

Pozostaje nam wyrazić współczynnik $K$ dla wahadła fizycznego. Można zauważyć, spoglądając na il. 5.7 i stosując przybliżenie małych drgań, które posłużyły do wyprowadzenia wzoru na $F_{s}$ w przypadku wahadła matematycznego, że moment siły $M$ wynosi:

M=F_{s}l\approx mg\frac{x}{l} l\approx mgl\alpha

Zwróćmy uwagę, że zastosowane przybliżenie (w przypadku obu wahadeł) jest równoważne często stosowanemu przybliżeniu $\sin\alpha\approx\alpha$ . Przybliżenie to jest tym lepsze, im kąt $\alpha$ jest mniejszy. Dlatego nasze rozważania są stosowalne tylko dla niewielkich wychyleń.

Zatem, uwzględniając znak, mamy:

M=-mgl\alpha

( 5.21 )

Tak więc $K=mgl$ i zgodnie z (5.20):

\omega=\sqrt{\frac{mgl}{I}}

( 5.22 )

Okres $T=\frac{2\pi}{\omega}$ , więc z równania (5.22) otrzymamy wzór na okres $T$ wahań wahadła fizycznego:

T=2\pi\sqrt{\frac{I}{mgl}}

( 5.23 )

Zauważmy, że wzór (5.17) na okres drgań wahadła matematycznego wynika ze wzoru (5.23), jako jego szczególny przypadek. Istotnie, moment bezwładności wahadła matematycznego $I=ml^{2}$ (patrz tom II, rozdz. Dynamika bryły sztywnej). Po podstawieniu tego wyrażenia do wzoru (5.23), otrzymamy wzór (5.17).

EXE Doświadczenie: Ruch harmoniczny

Przykład 3

Wyznacz okres drgań wahadła fizycznego utworzonego przez jednorodny pręt o długości $L$ zawieszony na jednym z końców (il. 5.8).

Ilustracja 5.8. **Szczególne wahadło fizyczne – pręt zawieszony na jednym końcu**

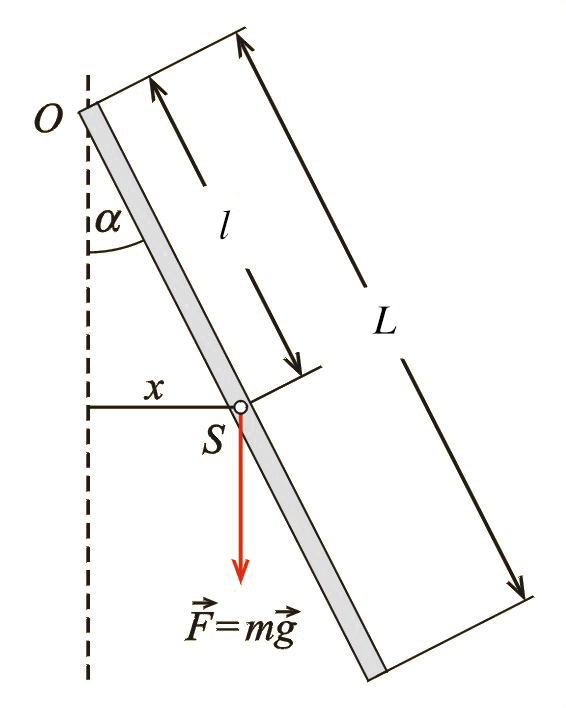
Rozwiązanie: Zastosujemy wzór (5.23):

T=2\pi\sqrt{\frac{I}{mgl}}

gdzie $l=\frac{L}{2}$ jest odległością środka masy pręta od punku zawieszenia. Moment bezwładności pręta względem środka masy wynosi $I_{0}=\frac{mL^{2}}{12}$ (wzór (4.23)). Stosując twierdzenie Steinera (rozdział 4.3 Twierdzenie Steinera. Zależność momentu bezwładności od położenia osi obrotu), otrzymamy moment bezwładności pręta względem jego końca: $I=I_{0}+m\left(\frac{L}{2}\right)^{2}=\frac{mL^{2}}{3}$ . Po podstawieniu do wzoru (5.23) otrzymamy:

T=2\pi\sqrt{\frac{I}{mgl}}=2\pi\sqrt{\frac{\frac{mL^{2}}{3}}{\frac{mgL}{2}}}=2\pi\sqrt{\frac{2}{3}\frac{L}{g}}

Widzimy, że okres tego wahadła jest $\sqrt{\frac{2}{3}}$ razy mniejszy od okresu wahadła matematycznego o takiej samej długości.

Pytania i problemy

Wyjaśnij, czym charakteryzuje się wahadło, które można nazwać wahadłem matematycznym. Wyprowadź wzór na okres drgań własnych tego wahadła.
Wyjaśnij, czym charakteryzuje się wahadło, które można nazwać wahadłem fizycznym. Wyprowadź wzór na okres drgań własnych tego wahadła.
Kulka ma promień r i jest zawieszona na nici o długości l w ziemskim polu grawitacyjnym g . Okres drgań tego wahadła wyrażono na dwa sposoby: T m – korzystając ze wzoru (5.17) oraz T f – korzystając ze wzoru (5.23).
1. Przypomnij sobie wzór na moment bezwładności kuli o promieniu $r$ oraz treść prawa Steinera i wykaż, że $T_{f}>T_{m}$ .
2. Wyprowadź warunek, jaki musi spełniać stosunek $\frac{r}{l}$ , by procentowa różnica między $T_{f}$ i $T_{m}$ była mniejsza niż 1%:
  
  $\frac{T_{f}-T_{m}}{T_{m}} \less 0,01$