1.D1. Dodatek: Ocena dokładności wyników pomiarów

Każdy wynik pomiaru $x$ daje tylko wartość przybliżoną rzeczywistej wartości $x_{0}$ . Powodowane jest to różnymi czynnikami, wśród których występują czynniki losowe, na które nie mamy wpływu. Przyjmujemy więc, że każdy pomiar odbywa się zawsze z ograniczoną dokładnością, wynikającą zarówno z okoliczności towarzyszących pomiarowi, bezpośrednich czynności pomiarowych, jak i z wykonania samego przyrządu pomiarowego; przy pomiarze długości występuje na przykład niedokładne przyłożenie linijki, nieprecyzyjne wykonanie podziałki, określona grubość kresek podziałki itd.

Mimo że prawdziwa wartość wielkości mierzonej nie jest znana, możemy określić przedział wartości, w którym się ona mieści. Połowę szerokości tego przedziału nazywamy niepewnością pomiarową $\Delta x$ . Przyjmujemy, że wartość rzeczywista mieści się w przedziale między $\left(x-\Delta x\right)$ a $\left(x+\Delta x\right)$ , gdzie $x$ jest wartością zmierzoną. Na przykład, mierząc długość pręta, otrzymaliśmy wartość $x=36,4\, cm$ i niepewność pomiarową $\Delta x=0,3\, cm$ . Przyjmujemy więc, że długość zmierzonego pręta wynosi $36,4\, cm\pm0,3\, cm$ .

Niepewności pomiarowe można zmniejszyć, stosując dokładniejszy przyrząd lub dokładniejszą metodę pomiaru, jednak nie jesteśmy w stanie ich całkowicie wyeliminować. Poza niepewnościami pomiarowymi występują błędy pomiarowe, których można uniknąć. Powstają często na skutek przeoczenia lub pominięcia ważnego czynnika wpływającego na pomiar, np. przy pomiarze długości pręta nie zauważamy jego wygięcia.

W celu zmniejszenia niepewności pomiarowej wykonujemy pomiar wielokrotnie, wtedy często poszczególne wyniki pomiaru nieco różnią się od siebie, gdyż każdy pomiar obarczony jest przypadkową niepewnością pomiarową. Obliczając średnią arytmetyczną tych pomiarów, otrzymujemy wartość najbardziej zbliżoną do wartości rzeczywistej. Czasami zdarza się, że jeden wynik pomiaru różni się znacznie od pozostałych. Wtedy odrzucamy go i nie uwzględniamy przy obliczaniu wartości średniej, gdyż mamy prawo sądzić, z dużym prawdopodobieństwem, że powstał na skutek błędu pomiaru. Mówimy, że ten wynik pomiaru jest obarczony błędem grubym.

Przy ocenie niepewności pomiarowych pojedynczego pomiaru bierzemy pod uwagę wszystkie czynniki, które wpływają na jego dokładność. Suma wszystkich przyczynków daje wypadkową niepewność pomiarową. Sposób oceniania niepewności pomiarowych zależy od konkretnej sytuacji.

Zastanówmy się teraz, jak obliczyć niepewność pomiarową w przypadku, gdy wynikiem pomiaru jest wielkość złożona, dana za pomocą wzoru matematycznego, którego elementami są wielkości obarczone niepewnością pomiaru.

Przykład: Pomiar obwodu blatu stołu

Mierzymy $l$ – obwód blatu stołu. Najpierw mierzymy długości poszczególnych krawędzi (il. 1.112). Otrzymaliśmy następujące wartości: $a=100,1\, cm$ , $b=60,0\, cm$ , $c=100,0\, cm$ i $d=59,8\, cm$ . Następnie dodajemy je do siebie, co daje obwód blatu:

l=a+b+c+d=319,9\, cm

Ilustracja 1.112. **Pomiar krawędzi stołu**

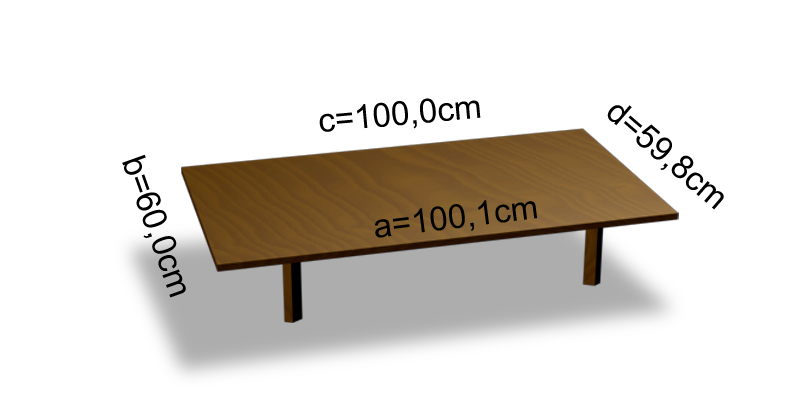
Mierzyliśmy miarką milimetrową z dokładnością $\pm2\, mm$ (wskazanie miarki odczytujemy dwukrotnie, na początku i na końcu mierzonej krawędzi), czyli pomiar krawędzi jest obarczony niepewnościami pomiarowymi $\Delta a=\Delta b=\Delta c=\Delta d=\pm0,2\, cm$ , zatem niepewność pomiaru obwodu wyniesie:

\Delta l=\Delta a+\Delta b+\Delta c+\Delta d=0,2\, cm+0,2\, cm+0,2\, cm+0,2\, cm=0,8\, cm

Wynik pomiaru zapisujemy w postaci:

l=\left(319,9\pm0,8\right)\, cm

Przykład: Pomiar długości ogrodzenia

Mierzymy $d$ – długość (w metrach bieżących) siatki, z której wykonano ogrodzenie domu. Najpierw mierzymy $d_{1}$ – długość całego ogrodzenia i odejmujemy od niej $d_{2}$ – szerokość furtki (il. 1.113). Otrzymaliśmy: $d_{1}=15,05\, m$ i $d_{2}=2,50\, m$ . Zatem długość siatki wynosi:

d=d_{1}-d_{2}=15,05\, m-2,50\, m=12,55\, m

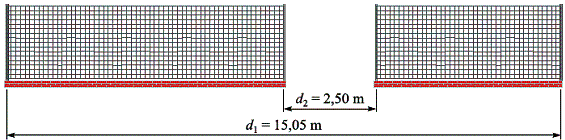
Mierzyliśmy taśmą mierniczą z podziałką 1 cm. Niepewność pomiaru przyjęliśmy jako równą 1 cm, czyli pomiar jest obarczony niepewnościami pomiarowymi $\Delta d_{1}=\Delta d_{2}=0,01\, m$ . Zatem niepewność pomiaru długości siatki ogrodzenia wyniesie:

\Delta d=\Delta d_{1}+\Delta d_{2}=0,01\, m+0,01\, m=0,02\, m

Niepewność pomiaru wyniku $\Delta d$ jest sumą niepewności składowych $\Delta d_{1}$ i $\Delta d_{2}$ , mimo że wynik pomiaru jest różnicą $(d=d_{1}-d_{2})$ . Postąpiliśmy tak celowo, ponieważ nie wiemy, czy pomiar bezpośredni jest obarczony niepewnością z plusem, czy z minusem. W takich sytuacjach powinniśmy uwzględniać najbardziej niekorzystny przypadek, gdy błędy się sumują.

Sposób postępowania w przykładach: Pomiar obwodu blatu stołu i Pomiar długości ogrodzenia uogólnimy następująco:

Jeżeli wynik pomiaru jest przedstawiony za pomocą wzoru w postaci sumy lub różnicy wielkości mierzonych bezpośrednio, to niepewność wyniku pomiaru jest równa sumie niepewności pomiarów bezpośrednich:

\Delta\left(x+y\right)=\Delta x+\Delta y

( 1.39 )

\Delta\left(x+y\right)=\Delta x+\Delta y

( 1.40 )

Przykład: Pomiar pola powierzchni blatu stołu

Mierzymy $S$ – pole powierzchni prostokątnego blatu stołu. Przyjmiemy, że blat jest prostokątny (pomiar przeciwstawnych krawędzi daje jednakowe wartości w granicach niepewności pomiaru). Przyjmiemy zatem, że prostokąt ma krawędzie $a=100,0\, cm$ i $b=59,9\, cm$ (są to wartości zaokrąglone średnie). Zatem pole powierzchni stołu wynosi:

S=ab=\left(100,0\, cm\right)\cdot\left(59,9\, cm\right)=5\,990,0\, cm^{2}

Jak w takim przypadku wyznaczyć niepewność pomiaru powierzchni stołu $Δ S$ ? Wydaje się, że można zastosować wzory (1.39) lub (1.40). To jednak błędne podejście, ponieważ wzory te dotyczą tylko sumy lub różnicy, a teraz mamy do czynienia z iloczynem. Gdybyśmy dodali niepewności w cm, to wynikowa niepewność również byłaby wyrażona w cm, a niepewność pomiaru pola musi być wyrażona w $cm^{2}$ .

Niepewność względna pomiaru to stosunek niepewności pomiaru do wielkości mierzonej:

\frac{\Delta x}{x}

Niepewność pomiarowa względna jest zawsze wielkością dodatnią. Tak więc formalnie jest to stosunek niepewności pomiaru do bezwzględnej wartości wielkości mierzonej:

\frac{\Delta x}{\left| x \right|}

. W zapisie na ogół opuszczamy wartość bezwzględną w mianowniku.

Niepewność pomiaru pola powierzchni blatu stołu wyznaczymy w taki sposób, że najpierw obliczymy wielkości niemianowane – niepewności względne $\left(\Delta a\right)/a$ i $\left(\Delta b\right)/b$ , a następnie ich sumę (również wielkość niemianowaną) uznamy za niepewność względną pomiaru pola. Zatem:

\frac{\Delta a}{a}+\frac{\Delta b}{b}=\frac{\Delta\left(ab\right)}{\left(ab\right)}=\frac{\Delta S}{S}

czyli:

\frac{\Delta S}{S}=\frac{\Delta a}{a}+\frac{\Delta b}{b}=\frac{0,2}{100}+\frac{0,2}{59,9}=0,0053

Ostatecznie:

\Delta S=\frac{\Delta S}{S}S=0,0053\cdot5990\, cm^{2}=32\, cm^{2}

Otrzymaliśmy w ten sposób niepewność pomiaru pola powierzchni stołu. Wynik pomiaru zapisujemy jako:

S=5\,990\pm32\, cm^{2}

Sposób postępowania w przykładzie Pomiar pola powierzchni blatu stołu uogólnimy następująco:

Jeżeli wynik pomiaru jest przedstawiony za pomocą wzoru w postaci iloczynowej, to względna niepewność wyniku pomiaru jest równa sumie względnych niepewności pomiarów bezpośrednich, co zapisujemy następująco:

\frac{\Delta\left(xy\right)}{\left(xy\right)}=\frac{\Delta x}{x}+\frac{\Delta y}{y}

( 1.41 )

Wzór możemy interpretować następująco: w przypadku iloczynu dwóch mierzonych wielkości $x$ i $y$ niepewność względna wyniku $\frac{\Delta\left(xy\right)}{\left(xy\right)}$ jest sumą niepewności względnych: $\frac{\Delta x}{x}$ i $\frac{\Delta y}{y}$ . Analogiczne rozumowanie pozwala wykazać, że w przypadku ilorazu dwóch mierzonych wielkości $x$ i $y$ niepewność względna wyniku wyraża się w ten sam sposób, czyli jako suma niepewności względnych.

Niepewność pomiaru wielkości złożonej wyrażonej w postaci:

sumy $X=x_{1}+x_{2}$ lub różnicy $X=x_{1}-x_{2}$ :

$\Delta X=\Delta x_{1}+\Delta x_{2}$
iloczynu $X=x_{1}\cdot x_{2}$ lub ilorazu $X=x_{1}\cdot x_{2}$ :

$\frac{\Delta X}{X}=\frac{\Delta x_{1}}{x_{1}}+\frac{\Delta x_{2}}{x_{2}}$

Zaokrąglenia wyników pomiarów

Na zakończenie przedstawimy jeszcze sposób zaokrąglania wyników i niepewności pomiarowych.

W przypadku gdy wartość niepewności pomiarowej ma pierwszą cyfrę znaczącą mniejszą od 3, podajemy ją z dokładnością do dwóch miejsc znaczących, w pozostałych przypadkach zaokrąglamy ją do jednej cyfry znaczącej.

Zero jest tylko wtedy cyfrą znaczącą, gdy znajduje się między dwiema cyframi niebędącymi zerami albo na dowolnym miejscu po cyfrze niebędącej zerem, zawartej w liczbie z przecinkiem. Taki sposób zaokrąglania wynika z faktu, że zwykle nie jesteśmy w stanie wyznaczyć niepewności pomiarowej z dużą dokładnością. Oto przykłady właściwych zaokrągleń niepewności:

0,00132\thickapprox\cong0,0013=1,3\cdot10^{-3}

0,0101\cong0,010=1,0\cdot10^{-2}

0,0301\cong0,03=3\cdot10^{-2}

6\,280\cong6\cdot10^{3}

Oto przykłady wyników pomiaru prawidłowo zaokrąglonych:

l=\left(1,4832\pm0,0013\right)\, m

m=\left(380\pm40\right)\, g

t=\left(86,5\pm0,6\right)\cdot10^{6}\, s