2.2. Druga zasada dynamiki Newtona
Siła
Co to jest siła? Dotychczasowe doświadczenie wykazuje, że wszystkie ciała oddziałują na siebie. Ciała stałe znajdujące się w naszym otoczeniu nie rozsypują się na części, ponieważ te części przyciągają się siłami spójności. Cząsteczki kropli cieczy również przyciągają się wzajemnie, chociaż słabiej. Powietrze w nadmuchanym baloniku oddziałuje na gumową powłokę balonika, napinając ją. Namagnesowane ciała oddziałują na siebie. Wszystkie ciała na Ziemi podlegają przyciąganiu przez nią. Ziemia przyciąga Księżyc itd.
Początkowo pojęcie siły powstało z oceny napięcia mięśni. Do dzisiaj używamy takich wyrażeń, jak silny człowiek, wysiłek mięśni itp. Później rozszerzono zakres tego pojęcia i używano go w takich wyrażeniach, jak siła woli, siła ducha, siły witalne i tym podobne. Wszystkie te wyrażenia – z punktu widzenia nauki – są nieprecyzyjne i ze stosowanym w fizyce pojęciem siły mają mało wspólnego. W fizyce siła jest to wielkość fizyczna, określająca jak duże jest oddziaływanie (przyciąganie lub odpychanie) między określonymi ciałami.
Zgodnie z tym, co powiedziano w rozdziale wstępnym, wszystkie rodzaje sił mają źródło w czterech podstawowych oddziaływaniach: grawitacyjnym, elektromagnetycznym, jądrowym i słabym. Mechanika obejmuje różne siły, ale w zasadzie wszystkie te siły, jak się przekonamy, dadzą się sprowadzić do dwóch rodzajów oddziaływań – grawitacyjnego i elektromagnetycznego.
Podstawą określenia siły jako wielkości fizycznej, zgodnie z tym, co zaznaczono w rozdziale wstępnym, powinien być dokładny przepis umożliwiający pomiar siły. Tylko w ten sposób można otrzymać ścisłą definicję siły.
Uogólniając wyniki wielu obserwacji i doświadczeń, stwierdzono, że mechanicznym skutkiem wzajemnego oddziaływania ciał mogą być:
- odkształcenie (deformacja) ciała (skutek statyczny), lub
- przyspieszenie (zmiana wartości lub kierunku prędkości) ciała (skutek dynamiczny).
Oczywiście, skutki te mogą występować również jednocześnie. Każdy z nich może służyć do pomiaru siły. W praktyce łatwiej jest mierzyć odkształcenie niż przyspieszenie. Dlatego do pomiaru siły stosuje się zwykle siłomierz (il. 2.7), w którym miarą działającej siły jest wartość wydłużenia sprężyny.

Sprężyna szczególnie nadaje się do pomiaru siły, ponieważ wykazuje proporcjonalność między wartością przyłożonej siły a wydłużeniem sprężyny (stanowi to treść prawa Hooke’a w odniesieniu do sprężyny, która podlega odkształceniom sprężystym, to znaczy znikającym po ustaniu działania siły).
Dla sprężyny obowiązuje następująca zależność:
gdzie – początkowa długość sprężyny, – długość sprężyny odkształconej, – współczynnik proporcjonalności, zwany współczynnikiem sprężystości. Widzimy więc, że siłę możemy wyznaczyć, mierząc odkształcenie sprężyny .
Siła jest wektorem. Jeżeli na jakieś ciało działa kilka sił, to wypadkową siłę możemy wyznaczyć, korzystając z zasady składania wektorów. Każdą siłę możemy rozłożyć na siły składowe wzdłuż określonych kierunków, jak również możemy rzutować siłę na wybrany kierunek.
Jedną z najbardziej popularnych sił jest siła ciężkości (pojęcie siły ciężkości będzie szczegółowo omówione w ramach prawa powszechnego ciążenia, któremu poświęcony jest rozdział Ciążenie powszechne (grawitacja)). Jest to siła, z jaką Ziemia przyciąga do siebie inne ciała. Z siłą ciężkości spotykamy się na co dzień. Wiemy, że wszystkie ciała spadają na Ziemię, jeżeli temu ruchowi nie przeszkadzają jakieś inne ciała. Siłę ciężkości odczuwamy bezpośrednio wtedy, gdy podnosimy przedmioty o dużej masie. Mówimy, że podnosimy ciężary.
Ciężar w nauce o siłach ma jednoznaczną definicję – ciężar ciała jest siłą, z jaką ciało to jest przyciągane grawitacyjnie przez inne ciała. W naszym codziennym doświadczeniu jest to siła przyciągania ciała przez Ziemię (ściśle: ciężar ciała jest równy sile wypadkowej siły ciążenia i siły bezwładności wynikającej z ruchu układu odniesienia. Siły bezwładności będą omówione w podrozdziale 2.8. Doświadczenie „Inercja”). Siłę tę możemy z łatwością mierzyć, posługując się odpowiednio wyskalowanym siłomierzem i stosując wzór (2.1). Miarą siły ciężkości jest wtedy odkształcenie sprężyny siłomierza, na którym zawieszono dane ciało.
Wiemy, że wszystkie ciała, niezależnie od wartości ich masy, w pobliżu Ziemi (w próżni) spadają ruchem jednostajnie przyspieszonym z jednakowym przyspieszeniem – przyśpieszeniem ziemskim . Natomiast wykonując proste doświadczenie – zawieszając na siłomierzu ciała o różnej masie, przekonujemy się, że wartość siły ciężkości zależy wprost proporcjonalnie od masy ciała :
Przyspieszenie ziemskie jest nieco inne w różnych miejscach na Ziemi – jego wartość zależy od szerokości geograficznej oraz od wysokości. Dla każdego z tych miejsc obowiązuje taka sama zależność (2.2). Ale ciężar ciała o ustalonej masie w różnych miejscach przyjmuje nieco inne wartości, proporcjonalne do miejscowego przyspieszenia ziemskiego:
Widzimy więc, że ciężar ciała jest proporcjonalny zarówno do jego masy, jak i do przyspieszenia ziemskiego. Zatem te dwie zależności (2.2) i (2.3) można zapisać w postaci jednej wspólnej: . Czyli , gdzie jest stałym współczynnikiem proporcjonalności zależnym od doboru jednostek. Jeżeli zastosujemy układ jednostek SI, w którym siłę wyraża się w niutonach, to . Zatem:
Napisaliśmy tę zależność w postaci wektorowej, ponieważ siła i przyspieszenie są wektorami (masa jest skalarem). Równanie to, jak się przekonamy, jest szczególnym przypadkiem ogólnego prawa – drugiej zasady dynamiki Newtona, która zostanie dokładnie rozpatrzona niżej.
Równanie (2.4) ma duże znaczenie praktyczne, gdyż pozwala mierzyć masę różnych ciał przez porównanie ich ciężarów. Pomiarów tych możemy dokonywać za pomocą siłomierza czy wagi sprężynowej lub stosując wagę szalkową. Widzimy, że słowo „ważenie” używane jest w dwóch różnych znaczeniach – jako pomiar ciężaru (czyli siły) albo masy.
Doświadczenie „Sprężyna”
Zadanie nasze polega na sprawdzeniu doświadczalnym wzoru (2.1) dla sprężyny. Doświadczenie wykonujemy w następującej kolejności:
Zawieszamy pionowo sprężynę i mierzymy długość . Zawieszamy ciężarek o określonej masie , więc i o określonym ciężarze . Sprężyna ulegnie rozciągnięciu pod wpływem siły ciężkości ciężarka. Mierzymy miarką milimetrową długość naciągniętej sprężyny. Następnie doczepiamy drugi taki sam ciężarek o tej samej masie i mierzymy aktualną długość sprężyny . Czynności te powtarzamy, podwieszając trzeci, czwarty i piąty ciężarek.

Wyniki pomiarów wpisujemy do tabelki pomiarów – il. 2.9.
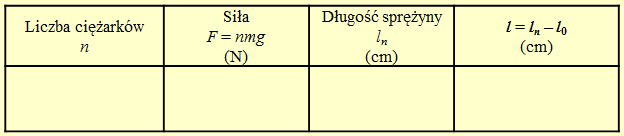
Sporządzamy wykres zależności od z uwzględnieniem niepewności pomiarowych długości sprężyny.
Cieszymy się, jeżeli punkty doświadczalne rozmieszczone są wzdłuż linii prostej, gdyż w ten sposób uzyskujemy potwierdzenie doświadczalne wzoru (2.1). Dzięki temu możemy wyznaczyć, bezpośrednio z wykresu, współczynnik sprężystości sprężyny , bowiem zgodnie ze wzorem (2.1) jest on liczbowo równy tangensowi kąta nachylenia tej prostej do osi odciętych.
Na koniec zapisujemy wnioski, jakie wynikają z przeprowadzonego doświadczenia.
Druga zasada dynamiki Newtona
Galileusz wykazał, że siła nie jest potrzebna do podtrzymania ruchu jednostajnego ciała po linii prostej. Newton ujął to w postaci prawa bezwładności jako pierwszą zasadę dynamiki. Newton jednakże poszedł dalej od swojego poprzednika, stwierdzając, że siła nie jest potrzebna do podtrzymania ruchu jednostajnego i prostoliniowego, ale jest konieczna do zmiany wektora prędkości ciała. Żadna zmiana prędkości nie zajdzie, jeżeli nie zadziała na ciało siła. Innymi słowy, siła działająca na ciało wywołuje zmianę prędkości, czyli nadaje mu przyspieszenie. To właśnie jest treścią drugiej zasady dynamiki Newtona. Było to genialne odkrycie, które pchnęło naukę na nowe tory. Prawo to wydaje się nam dzisiaj niezwykle proste i dostrzeżenie tej prawdy w wielu zjawiskach wydaje się łatwe. Jednakże w owym czasie była to myśl nowatorska i musiała pokonać uprzedzenia narosłe przez całe stulecia.
Jest to podstawowe równanie dynamiki, które ma niezwykle szeroki zasięg. Prawo to sprawdza się we wszystkich zjawiskach mechanicznych makroskopowych i mikroskopowych na Ziemi i w Kosmosie.
Jedynie dla bardzo dużych prędkości, zbliżonych do prędkości światła, wzór (2.5) ulega pewnej modyfikacji wynikającej z teorii względności Einsteina.
Wzór (2.5) pozwala na zdefiniowanie jednostki siły, którą na cześć Newtona nazwano niutonem. Jeden niuton jest to siła, która ciału o masie nadaje przyspieszenie :
Do niedawna bardzo rozpowszechnioną jednostką siły był (i jest ciągle jeszcze stosowany) tzw. kilogram-siła, . Jest to siła, z jaką Ziemia przyciąga ciało o masie w miejscu, gdzie przyspieszenie ziemskie . Zatem:
Przykład 1
Obliczymy, z jaką siłą pocisk o masie jest wyrzucany z lufy karabinu o długości , wiedząc, że prędkość pocisku u wylotu lufy . Przyjmijmy, że ruch pocisku w lufie karabinu jest jednostajnie przyspieszony.

Rozwiązanie: Droga pocisku w ruchu jednostajnie przyspieszonym jest równa:
gdzie – przyspieszenie pocisku, – czas ruchu pocisku w lufie.
Prędkość pocisku po czasie wynosi:
Z tych dwóch równań (po wyeliminowaniu czasu ) otrzymamy:
skąd:
Siła działająca na pocisk . Zatem:
Jest to bardzo duża siła; odpowiada ona na Ziemi ciężarowi ciała o masie ponad pół tony! Można ją także ocenić przez porównanie z siłą występującą w następnym przykładzie.
Przykład 2
Dopuszczalne opóźnienie przy hamowaniu samochodu (przy którym samochód nie wpada jeszcze w poślizg) . Z jaką maksymalną siłą hamuje wtedy samochód o masie ?

Rozwiązanie: Siła hamowania , zatem:
Tak duża siła jest potrzebna do wyhamowania pędzącego samochodu, a jednak siła ta jest mniejsza od siły z poprzedniego przykładu wypychającej maleńki pocisk z lufy karabinu.
Pytania i problemy
- Jeszcze dzisiaj stosujemy w życiu codziennym wyraz siła w odniesieniu do wielu zjawisk niefizycznych. Jakim warunkom musi odpowiadać pojęcie siły, aby była ona wielkością fizyczną? Podaj przykład siły jako pojęcia fizycznego oraz niefizycznego pojęcia siły.
- Podaj przykłady statycznego i dynamicznego skutku działania siły.
- Wyjaśnij zasadę pomiaru wartości siły za pomocą siłomierza.
- Jakie doświadczenie należy wykonać, aby się przekonać, że w danym miejscu na kuli ziemskiej siła ciężkości działająca na ciała o różnej masie ma wartość wprost proporcjonalną do masy ciała?
- Czy siła jest wektorem? Odpowiedź uzasadnij.
- Uczeń stanął na wadze i stwierdził, że waga wskazała 65 kilogramów. Podaj fizyczną interpretację wyniku tego pomiaru.
- Podaj treść drugiej zasady dynamiki Newtona i odpowiedni wzór.
- Przyjmując, że samolot odrzutowy podczas rozpędzania się przy starcie porusza się ruchem jednostajnie przyspieszonym, oblicz z jaką siłą działają jego silniki. Masa samolotu wynosi 10 000 kg, droga rozbiegu: 500 m, czas rozbiegu: 25 s.
- Porównaj siłę silników samolotu przy starcie (pytanie 8.) z siłami z przykładów Przykład 1 i Przykład 2. Sformułuj wnioski wynikające z tego porównania.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
