2.7. Atomowe orbitale elektronowe – bardziej zaawansowane wyobrażenie atomu (rozdział nadobowiązkowy)
Orbitale atomowe a orbity Bohra
Niełatwo jest porównać orbitale atomowe wodoru z orbitami elektronu w modelu Bohra. Trudności wynikają z dwóch zasadniczych różnic między tymi opisami.
1. W modelu Bohra elektron ma możliwość poruszania się tylko po kołowej orbicie, wykonuje więc jednowymiarowy ruch w płaszczyźnie. Dla każdego stanu określony jest promień orbity i prędkość elektronu. W modelu tym nie określa się orientacji tej płaszczyzny w przestrzeni. Mechanika kwantowa dopuszcza przebywanie elektronu w dowolnym punkcie trójwymiarowej przestrzeni, określając rozkład prawdopodobieństwa (inaczej: gęstość prawdopodobieństwa) występowania elektronu w poszczególnych punktach przestrzeni.
Stajemy zatem przed próbą porównania rozmiaru kołowej orbity z kształtem trójwymiarowej chmury prawdopodobieństwa, co już jest zadaniem karkołomnym. Na dodatek, próbujemy porównać pewność znalezienia krążącego po orbicie elektronu (w modelu Bohra), z szansą jego znalezienia w poszczególnych punktach przestrzeni (w modelu kwantowym).
2. W modelu Bohra stan atomu wodoru opisany jest jedną liczbą kwantową . Opis kwantowy (w najprostszej wersji, w której nie uwzględnia się spinu elektronu) wymaga wprowadzenia trzech liczb kwantowych, zwanych główną , orbitalną (albo poboczną) i magnetyczną . Wszystkie one określają kształt orbitalu, czyli rozkład prawdopodobieństwa występowania elektronu w przestrzeni wokół jądra. Jednak żadna z nich oddzielnie nie odpowiada jednoznacznie bohrowskiej liczbie .
Musimy więc, w celu porównania, przypisać każdej orbicie bohrowskiej kilka różnych orbitali atomowych. To podejście zastosujemy poniżej, pamiętając jednak, że takie przypisanie może być dość arbitralne. Innym wyjściem byłoby przypisywanie każdej orbicie bohrowskiej tylko jednego orbitalu, co też byłoby arbitralnym posunięciem. Na dodatek, wiele orbitali zostałoby wtedy wykluczonych z porównania.
Orbita a orbital 1s
Bohrowska orbita oraz orbital 1s (główna liczba kwantowa , poboczna i magnetyczna opisują stan podstawowy atomu wodoru, i dlatego możemy je powiązać. Promień pierwszej orbity dany jest wzorem (2.12), w którym ; wartość tego promienia to ok. 0,5 .
Orbital 1s jest sferycznie symetryczny. Oznacza to, że we wszystkich punktach leżących w jednakowej odległości od jądra (czyli na sferze), gęstość prawdopodobieństwa znalezienia elektronu jest jednakowa. Im bliżej jądra, tym gęstość ta jest większa, co pokazano na il. 2.37a. Oznacza to, że spośród wszystkich punktów w przestrzeni, największą szansę natrafienia na elektron mamy w okolicach jądra atomowego. Taki obraz nijak się ma do kołowej orbity elektronu o promieniu ok. 0,5 .
Możemy nieco inaczej spojrzeć na chmurę prawdopodobieństwa i zapytać o gęstość prawdopodobieństwa znalezienia elektronu w określonej odległości od jądra, czyli gdziekolwiek na powierzchni sfery o promieniu . Taka gęstość prawdopodobieństwa ma jednowymiarowy charakter (dokładniej: zależy od jednej zmiennej – ) i jest pod tym względem nieco bardziej podobna do orbity niż orbital. Chcąc uzasadnić zmianę gęstości prawdopodobieństwa znalezienia elektronu w zależności o promienia ( il. 2.37b), należy pamiętać, że pole powierzchni sfery o promieniu dążącym do zera także dąży do zera.Tak więc mimo zwiększającej się gęstości prawdopodobieństwa znalezienia elektronu w punkcie odległym o od jądra, szansa znalezienia go w określonej odległości od jądra maleje do zera, gdy ta odległość dąży do zera, co widzimy na il. 2.37. Na rysunku tym widać także, że po osiągnięciu maksymalnej wartości gęstość prawdopodobieństwa znalezienia elektronu maleje wraz ze zwiększającym się promieniem mimo coraz większego pola powierzchni sfery. Wynika to z bardzo szybko malejącej gęstości prawdopodobieństwa znalezienia elektronu w pojedynczym punkcie, co pokazano na il. 2.37a.
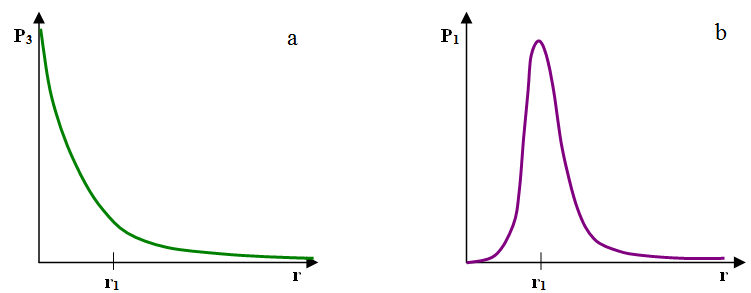
Ciekawą cechą orbitalu 1s jest położenie maksimum – przypada ono w odległości od jądra, równej promieniowi pierwszej orbity bohrowskiej. Zbieżność ta, zupełnie przypadkowa, nie uzasadnia jednak utożsamiania tej orbity i orbitalu ani nie jest podstawą do oceny trafności modelu Bohra.
Orbita a orbitale 2s i 2p
Bohrowska orbita , orbital 2s (w którym główna liczba kwantowa , poboczna i magnetyczna oraz 2p (w którym główna liczba kwantowa , poboczna , a magnetyczna może być równa -1, 0 lub +1) opisują pierwszy stan wzbudzony atomu wodoru, i dlatego możemy je powiązać. Promień drugiej orbity dany jest wzorem (2.12), w którym ; wartość tego promienia to ok. 2,1 .
Orbital 2s jest sferycznie symetryczny, podobnie jak orbital 1s. Gęstość prawdopodobieństwa znalezienia elektronu, jednakowa we wszystkich punktach leżących w jednakowej odległości od jądra, ma jednak bardziej skomplikowany przebieg, pokazany na il. 2.38a. Największą szansę natrafienia na elektron mamy, poszukując go w okolicach jądra atomowego. W pewnej odległości od jądra znajdują się punkty, w których szansa spotkania elektronu jest zerowa. Punkty te tworzą sferyczną powierzchnię nodalną wokół jądra, za którą zwiększa się szansa spotkania elektronu, osiąga lokalne maksimum, po czym maleje do zera. Obraz ten jest niepodobny do jakiejkolwiek orbity.
Podobnie jak w przypadku orbitalu 1s, możemy wykreślić jednowymiarową gęstość prawdopodobieństwa znalezienia elektronu w dowolnym miejscu na powierzchni sfery o promieniu . Przedstawiono to na il. 2.38b. Możemy z niego odczytać, że wyróżnione są trzy sfery: dwie, na których prawdopodobieństwo znalezienia elektronu osiąga lokalne maksimum, oraz jedna – znajdująca się pomiędzy nimi – sfera nodalna, na której to prawdopodobieństwo wynosi zero.
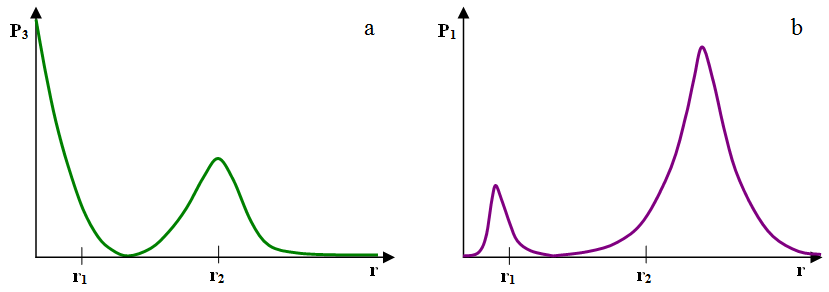
Orbital 2p nie ma sferycznej symetrii. Prawdopodobieństwo znalezienia elektronu w wybranym punkcie zależy nie tylko od odległości tego punktu od jądra, ale także od kierunku, w którym znajduje się ów punkt (kierunek ten jest określony w umownym układzie współrzędnych związanym z atomem). To znaczy, że wykresy analogiczne do tych na il. 2.37a i il. 2.38a mają nie tylko inny kształt, specyficzny dla orbitalu 2p. Dodatkowo, dla każdej wartości , rzędne tych wykresów mają różne wartości, zależnie od kierunku w jakim „odchodzilibyśmy” od jądra. Gdyby kołowa orbita miała taką cechę, to elektron, krążąc po niej – ruchem jednostajnym – na niektórych jej fragmentach o zadanej długości przebywałby częściej niż na innych, o takiej samej długości. Byłby to paradoks! W niektórych kierunkach gęstość prawdopodobieństwa wynosi zawsze zero – znalezienie elektronu w tych kierunkach jest niemożliwe. Brak sferycznej symetrii praktycznie uniemożliwia więc porównywanie tego orbitalu z kołową orbitą Bohra.
Orbitale o głównej liczbie kwantowej i większej mają symetrię sferyczną, gdy poboczna liczba kwantowa . Są one jednak jeszcze mniej podobne do orbit niż orbital 2s. Wraz ze zwiększaniem liczby n zwiększa się liczba lokalnych maksimów w gęstości prawdopodobieństwa znalezienia elektronu w punkcie odległym o od jądra (odpowiednik wykresów na il. 2.37a i il. 2.38a). Wskutek tego zwiększa się także liczba sferycznych powierzchni nodalnych, zlokalizowanych pomiędzy sferami, na których prawdopodobieństwo znalezienia elektronu osiąga lokalne maksimum (odpowiednik wykresów na il. 2.37b i il. 2.38b).
Doświadczenie
Naprzemiennie ułożone sfery nodalne i sfery o lokalnie maksymalnej gęstości prawdopodobieństwa można unaocznić w prostym eksperymencie. Potrzebna jest do niego długa (ok. 3–5 m) skakanka – taka, którą kręcą dwie osoby dla trzeciej, skaczącej. Dla uniknięcia kłopotów z synchronizacją, skakanką kręci jedna osoba (zwana operatorem), druga zaś swój koniec trzyma nieruchomo.
- Operator wprawia skakankę w typowy ruch obrotowy. Uzyskany obrazek jest podobny do orbitalu 1s – przyjmujemy, że unieruchomiony koniec skakanki to punkt na wykresie na il. 2.37b. Środkowy punkt skakanki, który zatacza okrąg o lokalnie największym promieniu, odpowiada punktowi na tym wykresie. Z kolei punkt, w którym operator trzyma skakankę i nią kręci, odpowiada bliżej nieokreślonemu (w tym modelu) punktowi na wykresie, leżącemu daleko na prawo od .
- Teraz operator zwiększa częstotliwość obrotu skakanką, starając się nie zmieniać jej naprężenia. Przy odrobinie wprawy uzyskuje się coś w rodzaju dwuosobowej skakanki. Jej obrót tworzy obraz nieco przypominający wykres na il. 2.38b. Jeden koniec skakanki (odpowiednik ) to punkt nodalny (inaczej węzłowy), po nim napotykamy punkt o lokalnie największym promieniu obrotu, dalej punkt „prawie nodalny” na środku skakanki (taki punkt, który praktycznie się nie porusza), kolejny punkt o lokalnie największym promieniu obrotu i wreszcie punkt obracany przez operatora. Podobieństwo nie jest pełne – lokalnie maksymalne promienie obrotu są praktycznie jednakowe, podczas gdy na wykresie na il. 2.38b wysokości dwóch lokalnych maksimów nie są takie same.
- Sprawny fizycznie operator nauczy się obracania skakanką z coraz większą częstotliwością, bez zmiany naprężenia skakanki. Przy niektórych, wybranych częstotliwościach obracana skakanka ułoży się wyraźnie w schemat skakanki trzy-, cztero- (a może nawet więcej?) osobowej. Uzyskane konfiguracje w przybliżeniu ilustrują rozkład gęstości prawdopodobieństwa znalezienia elektronu na sferze o promieniu wokół jądra dla orbitali, odpowiednio, 3s, 4s itd.
- Wsłuchanie się w rytm obracania skakanką pozwala wychwycić ciekawy fakt. Częstotliwość obrotów, przy której uzyskuje się skakankę dwu-, trzy-, cztero- itd. osobową, jest dwa, trzy, cztery itd. razy większa od częstotliwości dla skakanki jednoosobowej. Uzasadnienie takiego zachowania skakanki znajdziesz w rozdziale 5.12. Fale stojące, poświęconym falom stojącym, w III tomie podręcznika.
Orbitale o pobocznej liczbie kwantowej (np. 3p, 3d, 4p itd.) nie mają sferycznej symetrii, podobnie jak wspomniany wcześniej orbital 2p. Wyklucza to możliwość ich porównywania z kołowymi orbitami Bohra.
Przeprowadzone próby porównania bohrowskich orbit z podstawowymi cechami orbitali pokazują, że takie porównanie nie prowadzi do pouczających wniosków. Nie pozwala ocenić jakości modelu Bohra czy trafności jego przewidywań. Kwantowy obraz atomu nie daje się bowiem dokładnie „przetłumaczyć” na żaden opis klasyczny, choć niektóre przewidywania mogą być podobne. Przykładem niech będzie kwestia rozmiaru atomu: model Bohra przewiduje, że w kolejnych, coraz wyższych stanach wzbudzonych, promień orbity elektronu jest coraz większy. Do podobnej konkluzji prowadzi mechanika kwantowa, choć ujmuje ją inaczej: wraz ze zwiększaniem się głównej liczby kwantowej oraz liczby orbitalnej , szansa na znalezienie elektronu w punktach leżących blisko jądra maleje; tym samym zwiększa się szansa na jego znalezienie w punktach leżących coraz dalej od jądra.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
