5.10. Zasada Huygensa, ugięcie fali

Doświadczenie pokazowe 1

Wbijamy w cienką listewkę szereg szpilek równomiernie rozmieszczonych, np. co 5 mm (il. 5.24). Powstanie w ten sposób swego rodzaju „grzebień”. Uderzamy rytmicznie tym grzebieniem w powierzchnię wody. Zauważymy, że powstanie jedna fala płaska. Widzimy, że nałożenie się jednocześnie wzbudzonych fal kulistych, pochodzących z wielu położonych blisko siebie źródeł, daje wypadkową falę płaską.

Zastosowano tu nazwy: fala płaska i fala kulista, które dotyczą fal rozchodzących się w przestrzeni trójwymiarowej. Wprawdzie fale na powierzchni wody nie rozchodzą się w postaci fal przestrzennych, ale raczej powierzchniowych – dwuwymiarowych, to jednak powyższe pojęcia są przydatne i w tym opisie.

Fala płaska to taka fala, której czoło (powierzchnia falowa) jest płaszczyzną (w dwóch wymiarach – prostą).

Fala kulista to taka fala, której czoło (powierzchnia falowa) jest powierzchnią kulistą (w dwóch wymiarach – okręgiem).

Ilustracja 5.24. **„Grzebień” zbudowany w celu wywołania fali płaskiej na wodzie**

Im gęściej są położone źródła fal, tym bardziej fala wypadkowa będzie przypominać falę płaską. Najlepszy efekt otrzymamy, uderzając w wodę prostą cienką linijką.

W przestrzeni płaską powierzchnię falową otrzymamy, gdy źródła fal będą gęsto położone na wspólnej płaszczyźnie. Oczywiście, fala, której powierzchnia falowa jest płaszczyzną, nazywa się falą płaską. Tworzenie się fali płaskiej z wielu fal kulistych jest przedstawione na il. 5.25.

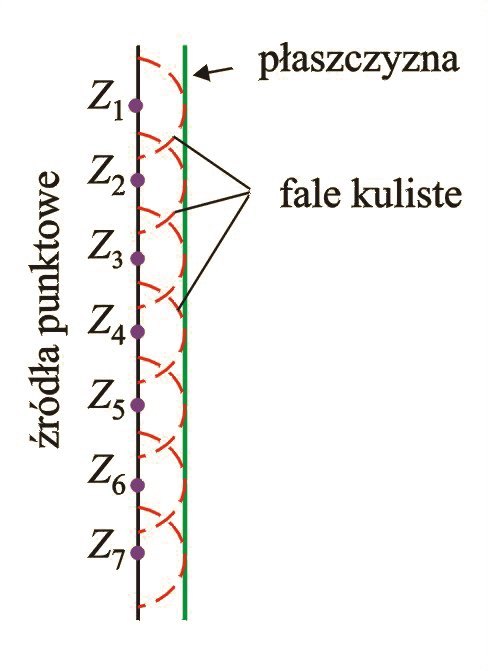
Ilustracja 5.25. **Tworzenie się fali płaskiej przez nakładanie jednocześnie pobudzonych fal kulistych, których źródła znajdują się na płaszczyźnie**

Wykonując doświadczenie 1, wyciągnęliśmy wniosek, że nałożenie szeregu fal kulistych może utworzyć falę płaską. Zatem można powiedzieć i odwrotnie – że płaską powierzchnię falową można rozłożyć na wiele fal kulistych. Po raz pierwszy zauważył to Christiaan Huygens (wym. hoejchens), fizyk holenderski, w drugiej połowie XVII wieku.

W ogólnym przypadku można udowodnić następującą zasadę, zwaną zasadą Huygensa:

To samo dotyczy fali jednowymiarowej. Gdy analizowaliśmy ruch fali na sznurze, doszliśmy do wniosku, że każda cząstka pobudzona do drgań przez falę sama pobudza następną do drgań, czyli staje się źródłem fali dla następnych cząstek sznura. Wniosek ten odniesiony do trzech wymiarów jest właśnie treścią zasady Huygensa.

Potwierdzenie tej zasady w dwóch wymiarach otrzymamy, wykonując poniższe doświadczenie.

Doświadczenie pokazowe 2

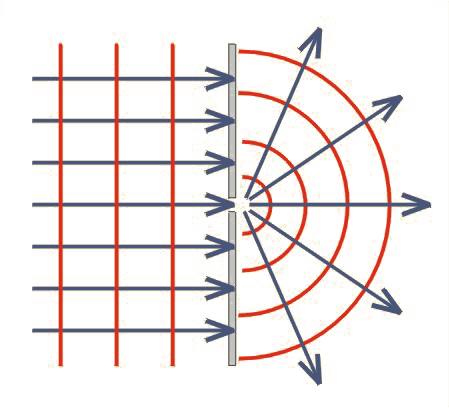
Wywołajmy na wodzie falę płaską i na jej drodze ustawmy przegrodę z wąską szczeliną, szerokości około 1 mm (którą możemy utworzyć, ustawiając obok siebie na przykład dwie deseczki), jak na il. 5.26. Za przegrodą utworzy się fala kulista. Wynik doświadczenia jest zgodny z zasadą Huygensa, gdyż spośród wszystkich punktów linii falowej wydzieliliśmy jeden, który stał się rzeczywiście źródłem nowej fali kulistej.

Ilustracja 5.26. **Otwór w przegrodzie, do którego dotarła fala, staje się źródłem nowej fali kulistej**

Tworzymy teraz w przegrodzie szerszą szczelinę (np. rozsuwając deseczki) i – podobnie jak poprzednio – przed przegrodą wzbudzamy falę płaską. Obserwujemy, że fala płaska przechodzi w tym samym kierunku, co przed przegrodą, ale w pobliżu krawędzi przegrody rozchodzi się kuliście (il. 5.27). Teraz widzimy, że zgodnie z zasadą Huygensa, spośród punktów położonych na linii falowej dwa skrajne ujawniły się jako źródła fal kulistych, na które nie nakładają się kolejne fale kuliste.

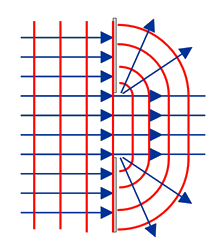
Ilustracja 5.27. **Na krawędziach przegrody ujawniają się fale kuliste**

Przyglądając się rezultatom powyższego doświadczenia, widzimy, że fala przed przegrodą poruszała się w określonym kierunku (prostopadłym do przegrody), a po przejściu przez przegrodę rozchodziła się także w nowych, zmienionych kierunkach. Zjawisko pojawiania się nowych kierunków rozchodzenia się fali w związku z obecnością przeszkody nazywamy ugięciem lub dyfrakcją fali na tej przeszkodzie.

Podkreślmy na koniec, że zjawisko ugięcia jest charakterystyczne wyłącznie dla ruchu falowego (dla rozchodzenia się fal). W ruchu makroskopowych korpuskularnych obiektów nie stwierdza się zmian kierunku ruchu ani pojawiania się nowych kierunków ruchu w związku z natrafieniem czy mijaniem jakiejkolwiek przeszkody. Żołnierz schowany za narożnikiem budynku nie jest narażony na pociski wystrzeliwane przez niewidocznego za murem nieprzyjaciela. Słyszy jednak wystrzały – fale dźwiękowe uginają się na przeszkodzie, jaką stanowi narożnik, zaś pociski kontynuują swój lot prosto albo zostają przez mur zatrzymane.

Pytania i problemy

Podaj treść zasady Huygensa.
Wyjaśnij, na czym polega zjawisko ugięcia fali na przeszkodzie.
Znana jest anegdota o człowieku, który wrzucał z mostu do wody kwadratowe płyty chodnikowe i dziwił się, że uzyskuje na wodzie „okrągłe” fale. Uzasadnij, korzystając z zasady Huygensa, efekt uzyskany przez owego człowieka; wykaż przy tym, że jego obserwacja była przybliżona. Wskazówka: Narysuj kilka powierzchni stałej fazy w kolejnych chwilach po uderzeniu płyty w wodę.