1.12. Odległości we Wszechświecie

Warto się zastanowić, w jaki sposób zdołano zmierzyć kosmiczne odległości, nie mając możliwości opuszczenia macierzystej planety.

Metoda triangulacyjna

Aby zmierzyć duże odległości, nie jest konieczne wybieranie się w podróż. Na Ziemi można obrać odcinek $A B$ (tzw. bazę triangulacji, il. 1.101), zmierzyć jego długość oraz kąty $\alpha$ i $\beta$ , pod którymi widać obiekt, aby dało się wyznaczyć odległości $(r_{A}$ i $r_{B})$ . Jak widać – punkty $A$ , $B$ i obiekt są wierzchołkami trójkąta; wystarczy zmierzyć jeden z boków trójkąta (tu $A B)$ oraz kąty $\alpha$ i $\beta$ , aby znaleźć długości pozostałych boków trójkąta $(r_{A}$ i $r_{B})$ . Trzeba także posłużyć się zasadą podobieństwa trójkątów lub jednym z twierdzeń trygonometrii.

Ilustracja 1.101. **Zasada triangulacyjnego pomiaru odległości obiektów astronomicznych**

Wystarczy znać jeden z boków trójkąta (tzw. bazę $d)$ oraz kąty $\alpha$ i $\beta$ przyległe do niego, aby znaleźć pozostałe boki trójkąta

Łatwo się o tym przekonasz, jeżeli wykonasz doświadczenie Pomiar metodą triangulacyjną.

Doświadczenie: Pomiar metodą triangulacyjną

Za pomocą metody triangulacyjnej, podobnej do tej, jaką stosują astronomowie, zmierzymy odległość punktu zaznaczonego na ścianie klasy od biurka nauczycielskiego, znajdującego się po przeciwnej stronie klasy. Biurko będzie spełniało rolę Ziemi, a punkt – wyobrażenie obiektu astronomicznego, np. Księżyca.

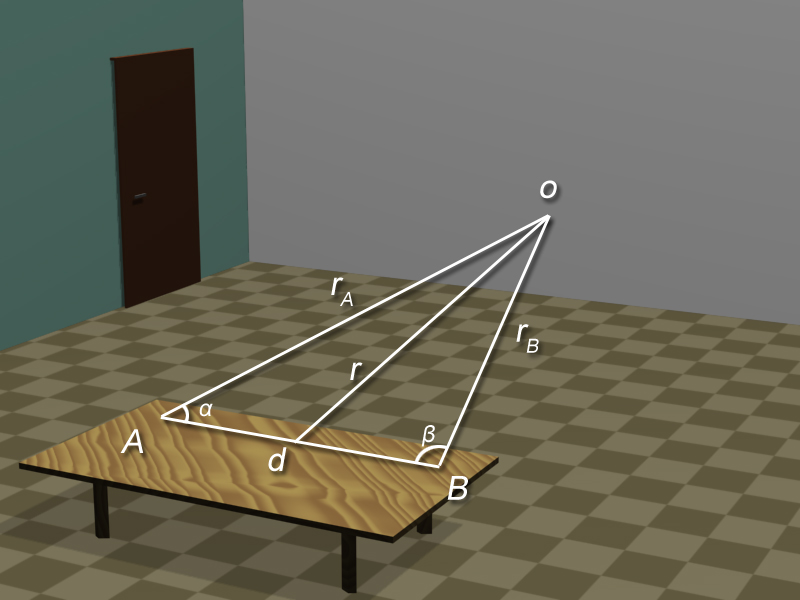
Na ścianie zaznacz (np. wbijając pinezkę) punkt $O$ (il. 1.102).

Narysuj kredą na biurku odcinek $A B$ równoległy do krawędzi stołu (il. 1.102). Będzie to baza do zdalnego pomiaru odległości do punktu $O$ .

Zmierz długość $d$ bazy – odcinka $A B$ – za pomocą taśmy mierniczej.

Zmierz kąty $\alpha$ i $\beta$ za pomocą kątomierza (np. takiego, który służy do rysowania kątów na szkolnej tablicy) lub lepiej – przyrządu optycznego do pomiarów kątów (np. teodolitu). W przypadku pomiarów kątomierzem umocuj (np. za pomocą plasteliny) cienki pionowy drut w środku kątomierza. Ustaw oko na linii łączącej drut z punktem $O$ . Trzymając w ręku drugi cienki drut, ustaw go na tej samej linii wzroku na kole kątomierza (przypomina to celowanie przed oddaniem strzału z karabinu, polegające na odpowiednim ustawieniu muszki i szczerbinki).

Każdy pomiar wykonaj trzykrotnie. Wyniki pomiarów wpisz do tabelki pomiarów wg wzoru (il. 1.103):

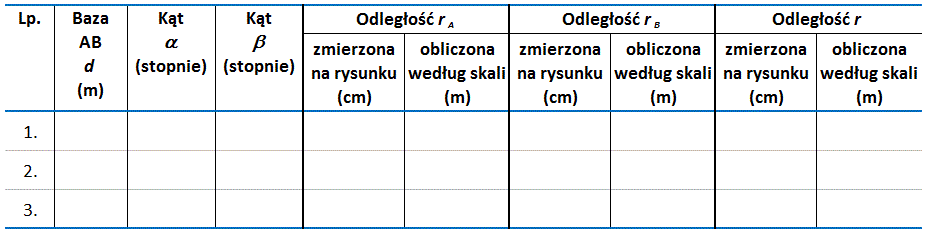
Przygotuj teraz trójkąt podobny do trójkąta $A B O$ , o odpowiednio mniejszych rozmiarach boków. Narysuj w skali, np. 1:20, na kartce papieru (np. formatu A3) bazę – odcinek $A B$ . Na przykład, jeżeli zmierzona długość bazy $d$ wynosi 1,6 m, to na rysunku w skali 1:10, ten odcinek będzie miał długość 16 cm, a w skali 1:20 – 8 cm.

Na papierze narysuj linie proste wychodzące z punktów $A$ i $B$ nachylone do bazy pod kątami $\alpha$ i $\beta$ . Miejsce przecięcia tych prostych oznacz jako punkt $O$ . Zmierz odcinki $r_{A}$ i $r_{B}$ , zastosuj odwrotność skali i oblicz rzeczywiste odległości $r_{A}$ i $r_{B}$ . Do obliczeń wykorzystaj wartości średnie z kilku (np. trzech) pomiarów. Wyniki pomiarów i obliczeń wstaw do tabelki. Przykładowe dane znajdują się w tabeli (il. 1.104).

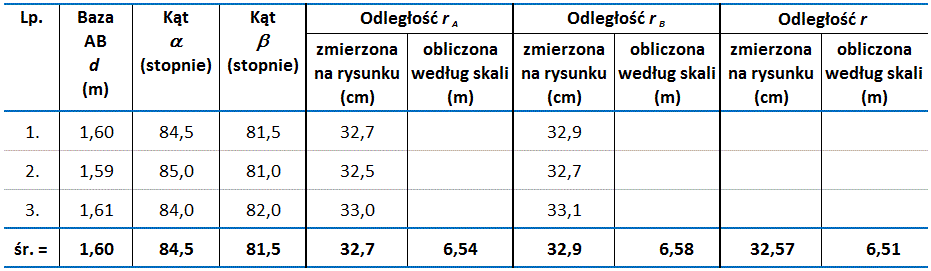
Ilustracja 1.104. **Tabela z przykładowymi wynikami pomiarów (skala rysunku 1:20)**

Wykonując to doświadczenie, masz możliwość sprawdzenia wyników $r_{A}$ , $r_{B}$ i $r$ za pomocą taśmy mierniczej, co oczywiście jest niewykonalne w przypadku pomiarów astronomicznych. Zmierz zatem za pomocą taśmy mierniczej odległości $r_{A}$ , $r_{B}$ i $r$ , a następnie porównaj je z wynikami otrzymanymi opisaną wyżej metodą graficzną. A oto przykładowe dane pomiarów wykonanych taśmą mierniczą:

Ilustracja 1.105. **Wyniki pomiarów wykonanych taśmą mierniczą**

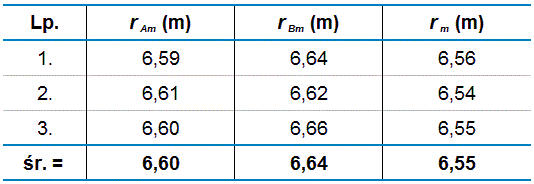
Po porównaniu wyników pomiarów podanych w tabeli na il. 1.105 z wynikami z tabeli na il. 1.104, widzimy, że:

\Delta r_{A}=r_{Am}-r_{A}=0,06\, m

\Delta r_{B}=r_{Bm}-r_{B}=0,06\, m

\Delta r=r_{m}-r=0,04\, m

Te wartości możemy uznać za wiarygodne oszacowanie niepewności pomiaru w naszej metodzie zdalnego wyznaczania odległości. Ujednolicając, możemy przyjąć, że niepewność naszego pomiaru odległości metodą triangulacyjną wynosi 0,06 m, więc niepewność względna jest rzędu 1%. Zatem końcowe wyniki pomiarów powinniśmy przedstawić w postaci:

r_{A}=(8,02\pm0,06)\, m

r_{B}=(8,10\pm0,06)\, m

r=(8,00\pm0,06)\, m

Doświadczenie „Triangulacja” umożliwia zapoznanie się z zasadą triangulacyjnego pomiaru odległości stosowaną w astronomii, bez znajomości wzorów trygonometrycznych. Poniżej jest opisana metoda, która wykorzystuje wzory trygonometryczne. Podstawowym narzędziem w tej metodzie jest tzw. twierdzenie sinusów, zgodnie z którym w dowolnym trójkącie na płaszczyźnie stosunek długości boku do sinusa kąta przeciwległego do tego boku jest jednakowy dla wszystkich trzech boków.

Po zastosowaniu twierdzenia sinusów do trójkąta $A B O$ z il. 1.102, otrzymujemy:

r_{A}=\frac{d}{\sin\left(\alpha+\beta\right)}\sin\beta

( 1.33 )

r_{B}=\frac{d}{\sin\left(\alpha+\beta\right)}\sin\alpha

( 1.34 )

Znajomość odległości Ziemia-Księżyc umożliwiła określenie rozmiarów Księżyca. Na rysunku poniżej (il. 1.106) wyjaśniono zasadę pomiaru średnicy Księżyca.

Ilustracja 1.106. Zasada pomiaru promienia Księżyca $r_{K}$

Znając

r

– odległość Ziemia–Księżyc i mierząc kąt

\alpha

(z pewnego punktu na Ziemi), możemy wyznaczyć

r_{K}=r \sin\alpha

Metoda paralaksy

Metody triangulacyjne można stosować tylko do niezbyt odległych obiektów. Tą metodą zmierzono odległości do Księżyca, planet Układu Słonecznego i do Słońca. Do najbliższych sąsiednich gwiazd stosuje się odmianę metody triangulacyjnej, tzw. metodę paralaksy. Metoda ta wykorzystuje zjawisko pozornej zmiany położenia przedmiotu oglądanego z różnych kierunków.

W związku z ruchem Ziemi wokół Słońca obraz bliskiej gwiazdy w ciągu roku zatacza na niebie elipsę. Po wielkości tej elipsy można poznać, jak daleko znajduje się gwiazda: im większa elipsa, tym gwiazda jest bliżej nas. Na Ziemi mierzymy tzw. paralaksę – kąt $\varepsilon$ (il. 1.107).

Na rysunku poniżej (il. 1.107) pokazano, jak wyznacza się odległość do gwiazdy z pomiaru tzw. paralaksy – kąta $\varepsilon$ , o który pozornie przemieszcza się bliska gwiazda na tle dalekich „gwiazd stałych”. Kąt ten wynika z ruchu Ziemi wokół Słońca w przypadku, kiedy stosuje się średnicę orbity Ziemi jako bazę – mierzymy położenie gwiazdy na tle odległych, nieruchomych gwiazd w dwóch momentach: gdy Ziemia znajduje się w przeciwnych miejscach na swojej orbicie wokółsłonecznej.

Odległość do gwiazdy $r$ można otrzymać ze wzoru:

r=\frac{r_{Z-S\mathchar'40\mkern-5mu l}}{\tg\varepsilon}

gdzie $r_{Z-Sl}$ jest odległością Ziemia-Słońce, której wartość jest równa 1 AU.

Ilustracja 1.107. **Metoda paralaksy**

Zasada wyznaczania odległości polega na pomiarze tzw. paralaksy – kąta $\varepsilon$ , o który pozornie przemieszcza się bliska gwiazda na tle dalekich „gwiazd stałych”. Bliska gwiazda w ciągu roku zatacza pełne kółko na niebie w związku z ruchem Ziemi wokół Słońca

Metodą paralaksy wyznaczono odległość do najbliższej znajdującej się poza Układem Słonecznym gwiazdy Proxima Centauri – wynosi ona 4,28 lata świetlne.

W astronomii odległości nie wyraża się w metrach czy kilometrach, gdyż jest to jednostka zbyt mała. Jednostki odległości używane w astronomii to:

AU – jednostka astronomiczna – średnia odległość od Ziemi do Słońca; $1\, AU=1,496\cdot10^{8}\, km$ ,
rok świetlny – droga, którą przebywa światło w próżni w czasie jednego roku; $1\, r.\acute{s}w.=1\, ly=9,46\cdot10^{12}\, km$ (oznaczenie ly pochodzi od ang. light year),
parsek – odległość, z której promień orbity ziemskiej widziany byłby pod kątem 1 sekundy łuku; $1\, ps=3,26\, ly=206\,265\, AU=3,086\cdot10^{13}\, km$ (nazwa parsek pochodzi ze skrótu słów angielskich: parallax 'paralaksa' i second 'sekunda').

Metoda świec standardowych

Pomiary odległości do obiektów kosmicznych znajdujących się znacznie dalej wykonuje się, korzystając z innych sposobów. Aby wyniki były jak najbardziej wiarygodne, posługujemy się nie jedną, ale kilkoma metodami. Można dzięki temu poprawić dokładność pomiarów, zmniejszając błędy i niepewności pomiarowe. Astrofizycy znają wiele metod wyznaczania dalekich odległości. Jedna z nich nosi nazwę metody świec standardowych (il. 1.108).

Ilustracja 1.108. **Zasada pomiaru odległości metodą świec standardowych**

Teleskop zbiera tylko część mocy promieniowanej przez obiekt – im dalej od obiektu, tym mniejsza część mocy jest zbierana. Zatem natężenie światła odbieranego przez teleskop zależy od odległości od obiektu o określonej mocy promieniowania. Jeżeli znamy odległość $r_{1}$ i mierzymy natężenie światła $I_{1}$ od obiektu, to możemy wyznaczyć nieznaną odległość $r_{2}$ po zmierzeniu natężenia $I_{2}$

Metoda ta wykorzystuje fakt, że światło dochodzące do nas od gwiazdy jest tym słabsze, im dalej się ona znajduje. Obiektyw zwierciadła teleskopu o określonej powierzchni zbiera więcej światła, gdy gwiazda jest bliżej nas, a mniej – gdy jest dalej. Wielkość strumienia światła wpadającego do teleskopu informuje nas o odległości do gwiazdy.

Wyobraźmy sobie aleję z latarniami ustawionymi w równych odległościach. Natężenie światła dochodzącego od kolejnych latarń jest coraz mniejsze wraz ze zwiększaniem odległości od latarni. Na podstawie pomiaru jego natężenia, można wyznaczyć odległość pod warunkiem, że znamy absolutną jasność źródła światła, czyli całkowitą energię promieniowania wysyłanego przez źródło. Musimy przy tym założyć, że wszystkie latarnie świecą z jednakową mocą.

Na il. 1.109 widzimy, że talerz zwierciadła teleskopu o powierzchni $\Delta S$ zbiera światło z większego kąta od bliskiej gwiazdy znajdującej się w odległości $r_{1}$ , niż w przypadku, gdy gwiazda znajduje się w większej odległości $r_{2}$ .

Ilustracja 1.109. **Zasada metody świec standardowych**

Talerz zwierciadła teleskopu o powierzchni $\Delta S$ zbiera światło z większego kąta bryłowego od bliskiej gwiazdy znajdującej się w odległości $r_{1}$ , niż w przypadku, gdy gwiazda znajduje się w większej odległości $r_{2}$

Zależność natężenia światła od odległości od obiektu można wyprowadzić, stosując następujące rozumowanie.

Natężenie światła $I$ definiujemy jako stosunek mocy $P$ światła przechodzącego przez powierzchnię $S$ – ustawioną prostopadle do kierunku jego rozchodzenia się – do pola tej powierzchni:

I=\frac{P}{S}

( 1.35 )

Teleskop zbiera tylko część mocy promieniowanej przez obiekt – im dalej od obiektu, tym mniejsza część mocy jest zbierana. Jeżeli znamy odległość $r_{1}$ od obiektu o określonej mocy promieniowania i zmierzymy natężenie światła $I_{1}$ , to możemy wyznaczyć niewiadomą odległość $r_{2}$ . Cała moc $P_{0}$ jest wysyłana przez obiekt we wszystkich kierunkach. Jeżeli otoczymy obiekt sferą o promieniu $r_{1}$ , czyli o powierzchni $S=4\pi r_{1}^{2}$ , to natężenie światła wyniesie:

I_{1}=\frac{P_{0}}{4\pi r_{1}^{2}}

( 1.36 )

Podobnie dla odległości $r_{2}$ :

I_{2}=\frac{P_{0}}{4\pi r_{2}^{2}}

( 1.37 )

Dzieląc stronami oba te równania, po przekształceniu otrzymamy:

r_{2}=r_{1}\sqrt{\frac{I_{1}}{I_{2}}}

( 1.38 )

Aby zmierzyć odległości dalekich galaktyk metodą świec standardowych, trzeba znać ich absolutne jasności. Tak się szczęśliwie składa, że w wielu przypadkach w galaktykach znajdujemy gwiazdy supernowe typu Ia. Supernowe typu Ia to taki specyficzny rodzaj eksplozji białego karła, dla której potrafimy dość dokładnie określić moc, z jaką promieniuje gwiazda. Jeśli w odległej galaktyce znajdziemy supernową typu Ia, to możemy, po zmierzeniu jej jasności, wyznaczyć odległość do tej galaktyki.

Astronomowie znają też inne obiekty, które mogą posłużyć jako tzw. świece standardowe. Są nimi cefeidy – pulsujące gwiazdy, których jasność zmienia się z okresem od kilku do kilkudziesięciu dni. Właściwości cefeid badała Henrietta Leavitt w roku 1912. Na podstawie obserwacji odkryła i wyjaśniła związek między okresem pulsacji gwiazd i ich jasnością absolutną, co miało wielkie znaczenie dla rozwoju astronomii, gdyż cefeidy służą od tamtej pory jako „świece standardowe”.

Warto wspomnieć, że obecnie z bardzo dużą dokładnością wykonuje się pomiary odległości do najbliższych obiektów za pomocą techniki laserowej. Na przykład, pomiar czasu przelotu promienia laserowego odbitego od powierzchni Księżyca pozwolił na wyznaczenie odległości do naszego satelity z dokładnością do kilku centymetrów.

Metody opisane powyżej pozwoliły na wyznaczenie odległości kosmicznych, przedstawionych w tabeli Charakterystyczne odległości w Kosmosie.

Tabela 1. Charakterystyczne odległości w Kosmosie
Odległość	Wartość w km	Czas przelotu światła
średnica Ziemi	12,8^.10³	0,04 s
Ziemia – Księżyc	3,8^.10⁵	1,28 s
Ziemia – Słońce	1,5^.10⁸	8,32 min
Słońce – Neptun	4,5^.10⁹	4,16 h
Słońce – najbliższa gwiazda (Proxima Centauri)	4,05^.10¹³	4,28 lat
średnica Drogi Mlecznej	1,1^.10¹⁸	1,2^.10⁵ lat
Słońce – najbliższa galaktyka (w Andromedzie)	2,1^.10¹⁹	2,3^.10⁶ lat
promień obserwowalnego Wszechświata	1,3^.10²³	13,8^.10⁹ lat

Pytania i problemy

Narysuj i wytnij z kartki papieru krążek o średnicy nie większej niż 1 cm. Zmierz możliwie dokładnie jego średnicę. Przylep go na szybie okna wtedy, gdy Księżyc będący w pełni znajdzie się naprzeciwko. Ustaw głowę w takiej odległości od szyby, aby przy otwartym jednym oku krążek dokładnie zasłaniał Księżyc – il. 1.111. Zmierz odległość oka od szyby. Znając odległość Ziemi od Księżyca $r=384\,400\, km$ , oblicz z podobieństwa trójkątów średnicę Księżyca (i jego promień).

$\frac{2R}{r}=\frac{d}{l}\rightarrow2R=r\frac{d}{l}$

Ilustracja 1.111. Sposób pomiaru $2R$ – średnicy Księżyca
Wyjaśnij, na czym polega pomiar odległości metodą paralaksy. Co trzeba znać, aby tą metodą zmierzyć odległość do gwiazdy? Wykonaj schematyczny rysunek.
Wyjaśnij, na czym polega pomiar odległości metodą standardowych świec. Co trzeba znać, aby tą metodą zmierzyć odległość do jakiejś galaktyki?
Podaj definicje jednostek odległości stosowanych w astronomii: roku świetlnego, jednostki astronomicznej i parseka.
Mając dane z tabeli Charakterystyczne odległości w Kosmosie, zbuduj model obserwowanego Wszechświata w mikroskali. Przyjmij, że Układ Słoneczny został zmniejszony do wielkości cząsteczki gazu 0,2 nm. W jakiej odległości od Słońca w tej skali znajdzie się najbliższa gwiazda, a w jakiej – najbliższa galaktyka? Uwaga: $1\, nm\,(nanometr)=10^{-9}\, m$ .