3.6. Reakcje jądrowe

Nazwa „reakcje jądrowe” została utworzona przez analogię do nazwy „reakcje chemiczne”. Ta ostatnia odnosi się do łączenia się atomów w cząsteczki, a także do łączenia się cząsteczek lub ich rozpadu. W tych przemianach zasadniczą rolę odgrywają siły elektryczne. Jądra – podobnie jak cząsteczki – mogą się łączyć i ulegać rozpadowi. Jednakże te przemiany zachodzą z udziałem sił nie tylko elektrostatycznych, ale także jądrowych. W zapisie reakcji jądrowych przyjęto konwencje zbliżone do stosowanych przy reakcjach chemicznych; wyróżnia się w nim substraty i produkty reakcji jądrowej. Z tego punktu widzenia rozróżniamy trzy podstawowe kategorie reakcji.

Reakcje syntezy (reakcje fuzji)
Łączyć mogą się pojedyncze nukleony lub ich układy (jądra), tworząc większe jądra atomowe lub przyłączając się do już istniejących jąder. Tego typu reakcje wymagają dużej energii, dlatego zachodzą m.in. we wnętrzu gwiazd, w bombach wodorowych i innych urządzeniach termojądrowych. Przykładem takiej reakcji jest łączenie się jąder deuteru i trytu (są to tzw. ciężkie izotopy wodoru) w jądro helu:

$_{1}^{3}T+_{1}^{2}D\rightarrow_{2}^{4}He+n$

( 3.26 )
Reakcje wymiany
Substratem jest pojedynczy nukleon lub niewielkie jądro (np. cząstka $\alpha$ ), drugim substratem jest inne jądro, ich połączeniu towarzyszy usunięcie z jądra innego nukleonu lub innej ich grupy (np. deuteronu). Takiego typu była pierwsza, zaobserwowana w roku 1919 przez Ernesta Rutherforda, reakcja jądrowa. Znajdujące się w powietrzu jądra azotu „bombardował” on cząstkami $\alpha$ emitowanymi przez źródło promieniotwórczego radu. W rezultacie tworzone były jądra tlenu i emitowane były protony, które wywoływały błyski światła w detektorze. Reakcja przebiegała według schematu:

$_{7}^{14}N+_{2}^{4}He\rightarrow_{8}^{17}O+p$

( 3.27 )
Reakcje podziału (reakcje rozszczepienia, rozpadu)
Substratem jest sporych rozmiarów jądro atomowe oraz pojedynczy nukleon, najczęściej neutron. Wśród produktów są dwa jądra atomowe porównywalnych rozmiarów oraz pojedyncze nukleony. Na ogół, gdy mówimy o reakcjach rozszczepienia, mamy na myśli rozszczepienie ciężkich jąder, na przykład uranu czy plutonu. Reakcje takie zachodzą w reaktorach jądrowych i bombach atomowych. W poniższym przykładzie jądro uranu, po wchłonięciu neutronu, dzieli się na jądra rubidu i cezu, a podziałowi towarzyszy emisja dwóch neutronów:

$_{92}^{235}U+n\rightarrow_{37}^{90}Rb+_{55}^{144}Cs+2n$

( 3.28 )

Podział na te trzy typy nie zawsze jest jednoznaczny – na przykład reakcję (3.27) można byłoby zaklasyfikować jako reakcję syntezy, gdyż powstaje w jej wyniku jądro tlenu, większe od jądra azotu.

Reakcjom rozszczepiania i syntezy poświęcimy dwa następne paragrafy. W tym paragrafie zapoznamy się z ogólnymi cechami reakcji jądrowych.

Transmutacja pierwiastków

Czy można zamienić jeden pierwiastek w inny? To pytanie zadawali sobie alchemicy. Przez wieki całe próbowali metodami chemicznymi wyprodukować złoto z pomocą cudownej substancji zwanej „kamieniem filozoficznym”. Nie wiedzieli jednak, że chemia na nic się tu nie przyda. Reakcje chemiczne dotyczą zjawisk na poziomie powłok atomowych i wiązań cząsteczkowych, a pierwiastek chemiczny to substancja, której nie da się zamienić w inną metodami chemicznymi.

Alchemicy próbowali wyprodukować złoto metodami chemicznymi. Do tego potrzebna jest wiedza z zakresu fizyki, i to fizyki jądrowej. To, że jakaś substancja jest złotem, jest określone liczbą protonów w jądrze atomowym. Jak długo liczba ta wynosi 79, mamy do czynienia ze złotem, ale kiedy ta liczba jest inna, to substancja ta złotem się nie stanie, choćbyśmy ją zalewali kwasami, podgrzewali czy poddawali działaniu innych substancji w procesach chemicznych. Dzieje się tak, ponieważ reakcje chemiczne zachodzą na skutek oddziaływań tylko między powłokami elektronowymi, których budowa zależy od liczby dodatnich ładunków w jądrach atomów biorących udział w tych reakcjach.

Co innego w przemianach i reakcjach jądrowych. Tu może zmieniać się zarówno liczba masowa, jak i liczba atomowa jąder. Oznacza to, że można zmieniać jedne pierwiastki w inne, zgodnie ze schematami ich rozpadów lub równaniami reakcji jądrowych – zobacz, dla przykładu, przy opisie przemiany beta (rozdział 3.3. Przemiany jądrowe), w co zmieni się jądro kobaltu $_{27}^{60}Co$ , gdy wyemituje elektron. Zamianę jednego pierwiastka chemicznego w inny pierwiastek po raz pierwszy spowodował Rutherford, przeprowadzając reakcję (3.27).

Jądra złota można otrzymać, przykładowo, w wyniku reakcji wychwytu neutronu przez jadro rtęci $_{80}^{196}Hg$ w reaktorze jądrowym. Powstałe jądro $_{80}^{197}Hg$ następnie wychwytuje elektron z powłoki atomowej i zamienia się w jądro złota, emitując neutrino.

_{80}^{196}Hg+n\rightarrow{}_{80}^{197}Hg\,;\quad\quad\quad{}_{80}^{197}Hg+e^{-}\rightarrow_{79}^{197}Au+\nu

( 3.29 )

Trzeba tu jednak dodać, że otrzymywane tym sposobem złoto jest o wiele droższe od złota naturalnego, wydobywanego z ziemi. Co ciekawe, złoto znajdujące się w złożach mineralnych pochodzi też z reakcji jądrowych; zachodzących w gwiazdach supernowych. Z „popiołów” takich gwiazd powstała i nasza Ziemia.

Do transmutacji pierwiastków, czyli zamiany jednego pierwiastka chemicznego w inny, dochodzi także przy naturalnym rozpadzie jąder promieniotwórczych. Rozważmy reakcję:

_{92}^{238}U\rightarrow_{90}^{234}Th+_{2}^{4}He

( 3.30 )

Zastanówmy się, co dzieje się z jądrami uranu, które się rozpadły. Powstały z nich jądra toru; a te zaś – czy gdzieś znikają, rozpadają się dalej, czy może dzieje się z nimi jeszcze coś innego? Jądra, które się rozpadły i zmieniona została ich liczba atomowa, stają się innym pierwiastkiem chemicznym. W tym przykładzie są to nadal jądra promieniotwórcze, które dalej będą się rozpadać. W ten właśnie sposób tworzą się naturalne szeregi promieniotwórcze. Kolejne pierwiastki w takim szeregu mogą występować w innym stanie skupienia, np. z metalu może powstać gaz. Przykładem jest tworzenie się gazu radonu wskutek rozpadu radu. Na końcu szeregu promieniotwórczego znajduje się izotop stabilny.

Przykład: rozpad neptunu

W wyniku przemian jądrowych zapoczątkowanych rozpadem neptunu $_{93}^{241}Np$ powstaje trwały izotop bizmutu $_{83}^{209}Bi$ . Oblicz liczbę rozpadów $\alpha$ i $\beta^{-}$ .

Rozwiązanie: Cząstka $\alpha$ to cztery nukleony: 2 protony i 2 neutrony. Zatem cząstkę $\alpha$ można zapisać jako $_{2}^{4}\alpha$ .

Emisja z jądra jednej cząstki $\alpha$ pociąga za sobą stratę czterech nukleonów, czyli liczba masowa jądra zmniejsza się o 4 jednostki, oraz stratę dwóch protonów, więc ładunek jądra zmniejsza się o 2 jednostki.

Cząstka $\beta^{-}$ to elektron, który można zapisać jako $_{-1}^{0}\beta$ . Emisja z jądra jednej cząstki $\beta^{-}$ pociąga za sobą wzrost ładunku jądra o jedną jednostkę, a nie pociąga za sobą zmiany liczby masowej.

Widzimy więc, że w reakcji zamiany neptunu w bizmut było 8 przemian $\alpha$ oraz 6 przemian $\beta^{-}$ . Schematycznie możemy to zapisać następująco:

_{93}^{241}Np\rightarrow{}_{83}^{209}Bi+8{}_{2}^{4}\alpha+6{}_{-1}^{0}\beta

Bilans energii w reakcjach jądrowych

Podobnie jak w przypadku reakcji chemicznych, reakcje jądrowe mogą mieć charakter egzoenergetyczny bądź endoenergetyczny. W reakcjach pierwszego typu wydzielana jest energia, głownie w postaci energii kinetycznej produktów reakcji. W reakcjach endoenergetycznych konieczne jest dostarczenie energii – w postaci energii kinetycznej substratów – do ich przeprowadzenia.

Zasadnicza różnica między reakcjami chemicznymi i jądrowymi polega na ilości wydzielanej bądź pochłanianej energii. Zilustrujemy to na dwóch przykładach.

Przykład: energia wiązania

Energia wiązania jąder biorących udział w reakcji (3.26):

_{1}^{3}T+_{1}^{2}D\rightarrow_{2}^{4}He+n

wynosi odpowiednio: trytu $E_{T}=8,3\, MeV$ , deuteru $E_{D}=2,2\, MeV$ , helu $E_{He}=28,2\, MeV$ .

Przypomnij sobie niezbędne pojęcia z rozdz. 3.2. Własności jąder atomowych; zwróć przy tym uwagę na położenie jąder trytu, deuteru i helu na wykresie obrazującym zależność energii wiązania na jeden nukleon od liczby masowej jądra.

Oblicz energię $E$ wydzielaną przy syntezie jednego jądra helu z wodoru i trytu.

Rozwiązanie: Skorzystajmy z faktu, że w reakcjach jądrowych obowiązuje zasada zachowania energii, z uwzględnieniem defektu masy. Tak więc „energetyczny” zapis reakcji (3.26) wygląda następująco:

m_{T}\cdot c^{2}+m_{D}\cdot c^{2}=m_{He}\cdot c^{2}+m_{n}\cdot c^{2}+E

Masy poszczególnych jąder można wyrazić przez sumę mas nukleonów pomniejszoną o energię wiązania:

(m_{p}+2m_{n})\cdot c^{2}-E_{T}+(m_{p}+m_{n})\cdot c^{2}-E_{D}=(2m_{p}+2m_{n})\cdot c^{2}-E_{He}+mn\cdot c^{2}+E

Rozwiązując to równanie, zauważamy, że masy nukleonów się redukują; otrzymujemy:

E=E_{He}-E_{T}-E_{D}=17,7\, MeV

( 3.31 )

Porównajmy to z energią wydzielaną przy spalaniu cząsteczkowego wodoru w tlenie.

Przykład: energia wydzielona w reakcji chemicznej

Ciepło spalania wodoru $Q$ w chemicznej reakcji:

2H_{2}+O_{2}\rightarrow2H_{2}O

wynosi 143 MJ na każdy kilogram cząsteczkowego wodoru. Oblicz energię $2H_{2}+O_{2}\rightarrow2H_{2}O$ wydzielaną przy syntezie jednej cząsteczki wody.

Rozwiązanie: Masa molowa cząsteczkowego wodoru wynosi 2 g/mol. Oznacza to, że w jednym kilogramie wodoru znajduje się 500 moli tej substancji, czyli $500\cdot N_{A}$ cząsteczek wodoru. Symbolem $N_{A}$ oznaczamy tu liczbę Avogadra, czyli liczbę cząsteczek w jednym molu substancji; $N_{A}\approx6\cdot10^{23}$ sztuk. Tak więc ciepło spalania $Q'$ , odniesione do jednej cząsteczki wodoru, wynosi:

Q'=\frac{Q}{500\cdot N_{A}}=\frac{143\cdot10^{6}J}{500\cdot6\cdot10^{23}}\approx4,8\cdot10^{-19}J

Przypomnijmy, że energia 1 eV to $1,6\cdot10^{-19}J$ . Zatem $Q\text{’}=3\, eV$ .

Widać więc, że energia wydzielona w reakcji chemicznej jest co najmniej o sześć rzędów wielkości mniejsza od wydzielanej w reakcji jądrowej. Ta orientacyjna relacja dotyczy wszystkich znanych reakcji.

Energia progowa reakcji

Oddziaływania jądrowe są krótkozasięgowe, więc ich udział w reakcji wymaga zbliżenia do siebie oddziałujących obiektów na odległość rzędu $10^{-14}m$ i mniejszą. Oznacza to, że dodatnio naładowane cząstki – substraty reakcji – muszą pokonać barierę wzajemnego odpychania elektrostatycznego. Należy więc choć jednemu z nich nadać energię kinetyczną większą od pewnej minimalnej energii, zwanej energią progową.

Problemu tego nie ma jednak w przypadku neutronów, które nie mając ładunku elektrycznego, mogą wniknąć do jądra nawet przy bardzo niewielkich prędkościach. Dlatego też wiele reakcji przeprowadza się z udziałem neutronu jako jednego z substratów. Dotyczy to zwłaszcza sytuacji, gdy drugim substratem jest ciężkie jądro: wraz ze wzrostem liczby atomowej $Z$ pole elektryczne wytwarzane przez jądro staje się coraz silniejsze.

Zasady zachowania w reakcjach jądrowych

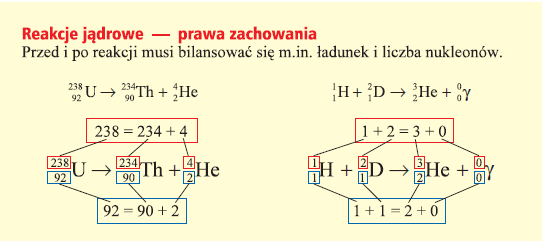
W reakcjach jądrowych muszą być spełnione znane już w fizyce klasycznej prawa zachowania:

energii – widzieliśmy w przykładzie Rozpad neptunu, że trzeba przy jego stosowaniu uwzględniać nie tylko energię kinetyczną substratów i produktów reakcji, ale także energię ich wiązania (defekty masy);
ładunku elektrycznego, w którym trzeba uwzględnić nie tylko dodatnie ładunki protonów, ale także dodatnie bądź ujemne ładunki ewentualnych elektronów czy pozytonów, emitowanych w przemianach $\beta$ ;
pędu i momentu pędu, które wymieniamy tu dla kompletności obrazu; z tymi dwiema wielkościami fizycznymi oraz zasadami ich zachowania zapoznasz się bliżej w rozszerzonym kursie fizyki.

W mikroświecie muszą być też spełnione prawa charakterystyczne dla procesów jądrowych, niemające swych odpowiedników w fizyce klasycznej. Wymienimy tu jedno z nich, które w odniesieniu do reakcji zachodzących przy niezbyt wysokich energiach można sformułować jako prawo zachowania całkowitej liczby nukleonów. Oznacza to, że liczba nukleonów przed i po reakcji musi być taka sama. Nie odnosi się to oddzielnie do protonów i neutronów. Może zmienić się liczba protonów, ale wtedy liczba neutronów musi się zmienić tak, by całkowita liczba nukleonów pozostała niezmieniona.

Ilustracja 3.62. **Ilustracja zasady zachowania ładunku elektrycznego i liczby nukleonów**

Jeśli w reakcji jądrowej dostępna jest energia rzędu gigaelektronowoltów i więcej, to może w niej dojść do produkcji antyprotonów i antyneutronów, a także innych krótko żyjących cząstek, (tzw. barionów). Są to, przykładowo, cząstki

\Delta

(delta),

\Lambda

(lambda),

\Sigma

(sigma),

\Xi

(ksi) i

\Omega

(omega); niektóre z nich mogą mieć różne ładunki: elementarne dodatnie, ujemne bądź zerowe. W takiej sytuacji obowiązuje zasada zachowania liczby barionów, przy czym antycząstkom przypisuje się „liczbę barionową” równą minus jeden.

Produkcja radioaktywnego węgla w atmosferze ziemskiej

W rozdziale 3.4. Prawo rozpadu promieniotwórczego, przy omawianiu metody datowania szczątków organicznych za pomocą izotopu węgla $_{6}^{14}C$ , zasygnalizowaliśmy pewien problem. Chodziło o stwierdzenie, czy zawartość tego izotopu w atmosferze jest stała. Tak w istocie jest, mimo iż jest to izotop promieniotwórczy, podlegający przemianie $\beta^{-}$ z czasem połowicznego zaniku ponad 5500 lat.

Izotop $_{6}^{14}C$ powstaje w górnych warstwach atmosfery w wyniku pochłonięcia neutronu przez jądro atomu azotu $_{7}^{14}N$ w reakcji wymiany:

_{7}^{14}N+n\rightarrow{}_{6}^{14}C+p

( 3.32 )

Neutrony powodujące tę reakcję albo pochodzą bezpośrednio z promieniowania kosmicznego (jest to strumień cząstek pochodzących przede wszystkim ze Słońca, składający się głównie z protonów, ale także z cząstek $\alpha$ i neutronów), albo powstają w wyniku oddziaływania innych składników tego promieniowania z jądrami atomowymi różnych pierwiastków obecnych w atmosferze. W każdym przypadku neutrony te obdarzone są odpowiednio dużą energią kinetyczną, by zapewnić przebieg reakcji (3.32), która jest endoenergetyczna. Tak długo jak aktywność Słońca pozostaje na niezmienionym poziomie – średnio rzecz biorąc w skali co najmniej tysięcy lat – stężenie neutronów w górnych warstwach atmosfery pozostaje praktycznie niezmienione. Zapewnia to stałe tempo powstawania jąder $_{6}^{14}C$ . Z drugiej strony, tempo ubywania tych jąder jest proporcjonalne do ich liczby. W efekcie powstaje stan równowagowy, w którym liczba jąder $_{6}^{14}C$ jest praktycznie stała w czasie.

Pytania i problemy

Określ liczbę masową $A$ , liczbę atomową $Z$ oraz symbol jądra $X$ powstającego w reakcji:

$_{13}^{27}Al+_{2}^{4}He\rightarrow{}_{Z}^{A}X+n$

Rozstrzygnij, czy jest to reakcja syntezy, reakcja wymiany, czy rozpad.
Zaproponuj sekwencję przemian $\alpha$ i $\beta^{-}$ , która doprowadzi izotop toru powstały w reakcji (3.30) do izotopu ołowiu $_{82}^{206}Pb$ . Wskazówka: nie jest tu istotna kolejność, w jakiej zachodzą przemiany $\alpha$ i $\beta^{-}$ ; dobierz odpowiednią liczbę przemian każdego rodzaju. Wykorzystaj do tego także Przykład: rozpad neptunu.
Rozpatrz następującą reakcję wymiany:

$_{7}^{14}N+{}_{Z}^{A}X\rightarrow{}_{6}^{14}C+{}_{Z'}^{A'}Y$
1. Nazwij cząstki $X$ i $Y$ , wiedząc, że są to najmniejsze możliwe jądra (ale nie pojedyncze nukleony!) spełniające warunki tej reakcji.
2. Przyjmij, że energia wiązania jądra azotu wynosi $E_{N}=104,1\, MeV$ , a jądra węgla $E_{C}=91,7\, MeV$ ; wyszukaj w tekście energię wiązania jąder $X$ i $Y$ . Rozstrzygnij, czy reakcja jest endoenergetyczna czy egzoenergetyczna. Oblicz energię wymienianą w tej reakcji.
Podaj jakościowy argument przemawiający za tym, że reakcja (3.32) jest endoenergetyczna. Wskazówka: Uwzględnij fakt, że jądro $_{7}^{14}N$ jest stabilne, natomiast jądro $_{6}^{14}C$ jest promieniotwórcze – podlega przemianie $\beta^{-}$ .