3.4. Prawo rozpadu promieniotwórczego
Wyobraźmy sobie próbkę zawierającą początkowo jąder promieniotwórczych. Jądro promieniotwórcze to takie, które może ulec przemianie (tutaj – przemianie , bądź ). Oczywiście, liczba jąder w próbce, które jeszcze nie uległy przemianie, maleje w czasie. Szybkość ubytku tych jąder w próbce określa prawo rozpadu promieniotwórczego, zwane także prawem zaniku liczebności próbki promieniotwórczej.
Jak maleje liczebność próbki promieniotwórczej?
Doświadczalne badanie próbek promieniotwórczych jąder pokazuje, że liczba jąder , które nie uległy przemianie po czasie , maleje tak jak pokazuje krzywa przedstawiona na il. 3.43.
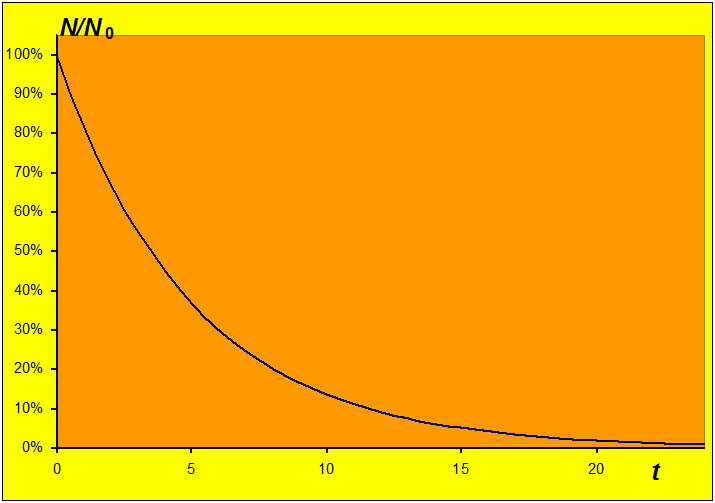
Wykres ten obrazuje prawo rozpadu promieniotwórczego. Zwrócimy uwagę na cztery jego cechy. Trzy pierwsze są widoczne „gołym okiem”:
- Zależność jest malejąca. Cecha ta jest oczywista: w miarę upływu czasu jakieś jądra atomowe się rozpadają, natomiast nie ma powodu, by do próbki dołączały „nowe” jądra.
- Wykres nie jest linią prostą. Liczba promieniotwórczych jąder pozostałych w próbce maleje nieliniowo wraz z upływem czasu. Uzasadnienie tej cechy podamy w dalszej części paragrafu; tutaj stwierdzimy tylko, że związana jest ona ze statystycznym charakterem rozpadu jądra (procesu emisji cząstki bądź z wnętrza jądra).
- Wykres nie osiąga wartości po żadnym określonym, z góry przewidywalnym czasie. Mówimy, że liczebność próbki dąży do zera asymptotycznie. Ta właściwość prawa rozpadu promieniotwórczego także wynika ze statystycznego charakteru zjawiska – nie da się przewidzieć, po jakim czasie pojedyncze jądro atomowe ulegnie przemianie.
Co to znaczy, że zjawisko rozpadu ma charakter statystyczny? Gdybyśmy nawet potrafili śledzić losy pojedynczego jądra w takiej próbce, to nie potrafilibyśmy przewidzieć, kiedy jądro to ulegnie „czekającej” je przemianie. Przyczyną jest to, że emisja cząstki czy z wnętrza jądra jest dziełem przypadku: może nastąpić po sekundzie, godzinie, roku... Mówimy, że proces emisji cząstki ma charakter statystyczny, zachodzi z określonym prawdopodobieństwem. Podobnie jest z wynikiem pojedynczego rzutu monetą: może ona upaść bądź „orłem” do góry, bądź „reszką” (każda z tych możliwości jest realizowana z prawdopodobieństwem 50%), ale wyniku pojedynczego rzutu nie da się jednoznacznie przewidzieć. Nie da się też przewidzieć, po ilu rzutach wreszcie uzyska się „orła”.
Jeśli jednak poprosimy wiele osób o jednoczesne wykonanie rzutu monetą, to możemy się spodziewać, że około połowa z nich uzyska „orła”. To oczekiwanie zostanie spełnione tym dokładniej, im więcej osób wykona taki rzut. Podobnie, jeśli będziemy obserwować liczebność całej próbki jąder promieniotwórczych, to stwierdzimy, że maleje ona w czasie według określonego „przepisu”, zwanego prawem rozpadu promieniotwórczego.
Czwarta cecha wykresu związana jest ze skalą czasową. Przyjrzymy się teraz bliżej tej problematyce.
Skala czasowa zaniku liczebności próbki jąder promieniotwórczych
Promieniotwórcze jądra atomowe pierwiastków różnią się prawdopodobieństwem rozpadu. Jeśli więc wyodrębnimy kilka próbek jąder różnych pierwiastków promieniotwórczych (w celu uproszczenia przyjmijmy, że początkowa liczba jąder jest taka sama), to wykresy ich liczebności w czasie nie będą się pokrywać, choć będą miały jednakowy „kształt”. Sytuacja taka jest przedstawiona na il. 3.44.
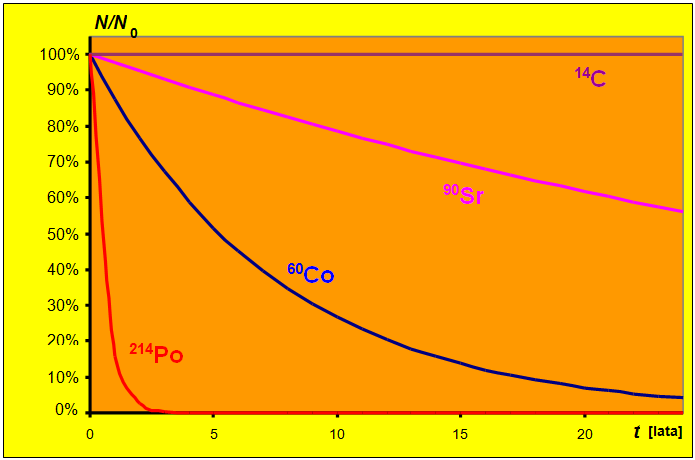
Linią niebieską oznaczyliśmy zanik jąder izotopu kobaltu . Rozpoznajemy w niej kształt z il. 3.43.
Jądra izotopu polonu charakteryzują się prawdopodobieństwem rozpadu ok. 14 razy większym niż jądra . Skutkiem tego jest znacznie szybszy zanik liczebności tej próbki: po około 3–4 latach spada ona – w skali wykresu – praktycznie do zera. Spadek ten jest tak szybki, że rozpoznanie charakterystycznego kształtu krzywej zaniku może wydawać się trudne.
Odwrotnie jest dla próbki jąder strontu : prawdopodobieństwo ich rozpadu jest ponad pięć razy mniejsze niż w przypadku jąder . W efekcie, zanik tej próbki jest znacznie wolniejszy; odnosimy wręcz wrażenie, że w skali dwudziestu kilku lat zanik ten jest jednostajny, choć uważne spojrzenie na wykres pozwala zauważyć nieliniowy jego charakter. Wreszcie ostatni izotop, , którego jądra mają prawdopodobieństwo rozpadu ok. 1000 razy mniejsze niż jądra . Tu widzimy, że w skali wykresu liczebność próbki praktycznie nie ulega zmianie – wnioskujemy, że upływ 20–30 lat w ogóle nie pozwala na zauważenie zaniku próbki.
Podsumujmy tę część rozważań następującym stwierdzeniem: dla każdego izotopu promieniotwórczego należy dobrać właściwą skalę czasu, w którym obserwowany jest zanik próbki. Skala ta związana jest z prawdopodobieństwem zajścia przemiany dla tego izotopu. W naszym przykładzie dogodnymi skalami czasowymi są: dla ok. 2 lata, dla ok. 30 lat, dla ok. 100–200 lat, zaś dla raczej dziesiątki tysięcy lat.
Czas połowicznego zaniku próbki jąder promieniotwórczych
Prawo rozpadu promieniotwórczego pozwala wyróżnić charakterystyczny czas zwany czasem połowicznego zaniku liczebności próbki (także okresem połowicznego zaniku próbki). Jest to czas, po którego upływie liczebność próbki maleje dwukrotnie. Oznaczamy go symbolem ; jest on wielkością charakteryzującą dany izotop promieniotwórczy.
Przykład: Ile jąder pozostanie w próbce?
Zastanówmy się, jaka część początkowej liczby jąder pozostanie promieniotwórcza po pięciu okresach połowicznego zaniku.
Rozwiązanie: Zauważ, że jedna czwarta, to , jedna ósma, to itd. Po pięciu okresach w próbce pozostanie więc , czyli początkowej liczby jąder. Oznacza to, że stosunek po upływie czasu wynosi 3,125%.
Korzystając z tych wyników, spróbujmy odpowiedzieć na bardziej ogólne pytanie: Ile jąder promieniotwórczych pozostanie w próbce po okresach, jeśli początkowa liczba jąder była ? Po okresach w próbce pozostanie liczba jąder promieniotwórczych dana wzorem:
Wzór ten pozwala przewidzieć liczebność próbki w dowolnej chwili . Wystarczy zauważyć, że liczba okresów połowicznego zaniku , to po prostu stosunek , gdzie jest czasem obserwacji. Czas ten niekoniecznie musi być równy całkowitej wielokrotności czasu połowicznego zaniku, więc niekoniecznie musi być liczbą całkowitą.
Badania rzeczywistych próbek jąder promieniotwórczych pokazują, że liczebność takich próbek zmienia się zgodnie z wykresem na il. 3.43 i zależnością (3.6). W następnym paragrafie przedstawimy i omówimy doświadczenie, którego przebieg jest uwarunkowany prawdopodobieństwem, podobnie jak rozpad jąder promieniotwórczych.
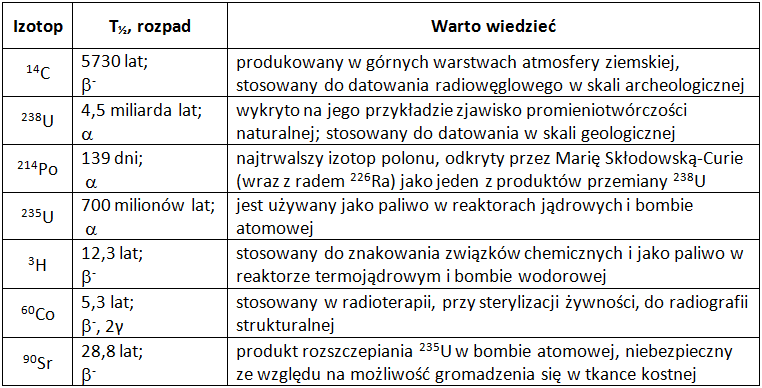
W przyrodzie występują różne izotopy promieniotwórcze, których czasy połowicznego zaniku zawierają się w bardzo szerokim zakresie: od nanosekund do miliardów lat. W tabeli (il. 3.45) ujęto kilka przykładowych izotopów, dla których podano czasy połowicznego zaniku wraz z nazwą rozpadu oraz wybrane informacje o nich.
„Naturalny zegar promieniotwórczy”. Datowanie izotopowe
Prawo rozpadu promieniotwórczego jest jak zegar, który tyka z czasem równym okresowi połowicznego zaniku. Jednym z bardziej znanych praktycznych zastosowań tego rozpadu promieniotwórczego jest datowanie. Jest to metoda oznaczania wieku minerałów lub przedmiotów pochodzących z odległych okresów historycznych bądź prehistorycznych, czyli sprzed tysięcy, milionów, a nawet miliardów lat. Jest ona stosowana m.in. przez historyków, archeologów i geologów. Datowanie izotopowe polega, w najprostszym ujęciu, na ustaleniu stosunku koncentracji wybranych izotopów promieniotwórczych do izotopów stabilnych w badanej próbce.
Każdy niemal słyszał o możliwości wyznaczenia wieku szczątków organicznych, np. roślin lub zwierząt, które żyły na Ziemi w okresie od kilkuset do kilkudziesięciu tysięcy lat temu. Wykorzystuje się do tego promieniotwórczy izotop węgla , którego okres połowicznego zaniku wynosi 5730 lat.
Węgiel jest jednym z podstawowych pierwiastków w organizmach żywych. Najczęściej jest to stabilny izotop węgla , ale w przyrodzie występuje też, choć w bardzo małych ilościach, promieniotwórczy izotop . Kiedy organizm żyje, to następuje w nim stale wymiana materii z otoczeniem i stosunek ilości izotopu węgla do ilości izotopu jest taki, jak w atmosferze. Kiedy jednak organizm żyć przestaje, zmniejsza się w nim ilość promieniotwórczego izotopu zgodnie z prawem rozpadu promieniotwórczego. Wykonując pomiar rozpadów promieniotwórczych w szczątkach organizmów żywych, można zbadać, jak zmienił się ten stosunek, a wykorzystując znaną wartość czasu połowicznego zaniku izotopu – ocenić wiek badanych szczątków.
Wzór (3.6) pozwala obliczyć liczebność próbki po czasie , gdy znamy początkową liczebność oraz czas połowicznego zaniku . Dokonajmy prostego „zabiegu”: zamieńmy wielkość szukaną w tym wzorze na daną, a w zamian niech będzie szukany czas . Wtedy mamy zadanie takie: „Określ czas , jaki upłynął od chwili, gdy liczebność próbki wynosiła , jeśli znasz oraz – jej liczebność obecną (czyli w chwili ). Dany jest także czas połowicznego zaniku tej próbki”. To zadanie trzeba rozwiązać.
Przykład: Oceniamy wiek przedmiotu
Stwierdzono, że próbka materii organicznej pobrana ze znalezionego podczas wykopalisk kawałka drewna zawiera trzy razy mniej izotopu (w porównaniu z izotopem ) niż w czasach współczesnych. Na podstawie wykresu z il. 3.47 oceń wiek artefaktu. Dla węgla czas połowicznego zaniku lat.
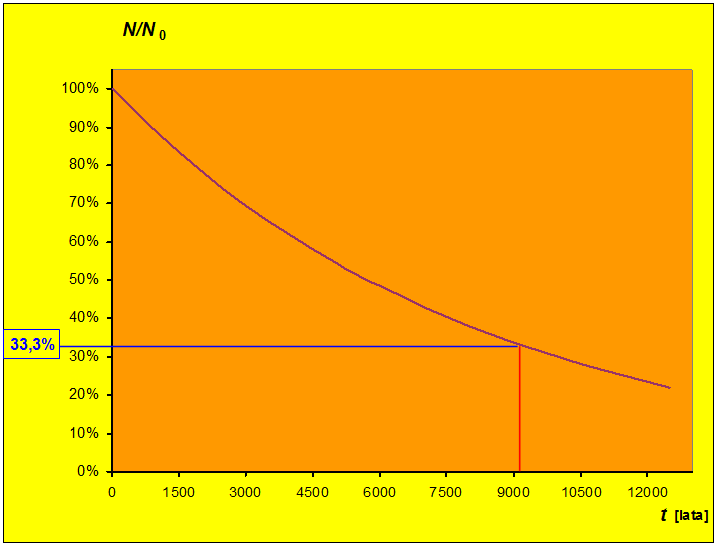
Rozwiązanie: Przyjmijmy, że zawartość w drzewie, z którego pochodzi znaleziony kawałek drewna, w chwili jego ścięcia dawno temu to umowne 100% na wykresie na il. 3.47. Obecnie zawartość ta zmalała trzykrotnie i stanowi 33,3% poziomu początkowego. Prowadzimy więc na wykresie poziomą linię (niebieską), odpowiadającą 33,3% na osi rzędnych i szukamy jej przecięcia z wykresem. Z tego punktu prowadzimy pionową linię (czerwoną) i odczytujemy z osi odciętych, że wiek artefaktu wynosi nieco ponad 9000 lat.
Komputerowe modelowanie zaniku promieniotwórczego (rozszerzenie wiadomości dla uczniów zainteresowanych fizyką)
Naturalne przemiany promieniotwórcze zachodzą spontanicznie, bez ingerencji zewnętrznych, w sposób losowy. Nie potrafimy przewidzieć, czy dane jądro rozpadnie się w określonym czasie, czy też nie. By więc opisać rozpad promieniotwórczy, musimy posłużyć się pojęciem prawdopodobieństwa, które najlepiej jest zdefiniować dla licznej próbki.
Obserwujemy próbkę jąder promieniotwórczych, powiedzmy, izotopu kobaltu , o liczebności ; po czasie stwierdzamy, że liczebność próbki zmalała do . Możemy wtedy powiedzieć, że prawdopodobieństwo rozpadu pojedynczego jądra kobaltu jest ilorazem liczby jąder , które się rozpadły, do liczby jąder , które miały taką możliwość:
W tym wzorze jest liczbą ujemną, gdyż oznacza różnicę między końcową liczebnością próbki a jej liczebnością początkową :
Tak zdefiniowane prawdopodobieństwo nie odzwierciedla, niestety, w sposób jednoznaczny właściwości jąder stanowiących naszą próbkę. Wynika to z faktu, że zależy ono od arbitralnie ustalonego odcinka czasu , po którym określamy liczebność . Przyjęto wobec tego zasadę przedstawiania prawdopodobieństwa w postaci iloczynu:
w którym określa jednoznacznie właściwości jąder . Wielkość tę nazywamy stałą rozpadu promieniotwórczego – każdy niestabilny izotop, podlegający którejkolwiek z poznanych przez nas przemian promieniotwórczych, charakteryzuje się określoną wartością . Z kolei taki zapis narzuca warunek na odcinek czasu : musi on być na tyle krótki, by zachować warunek . Dla potrzeb takich, jak komputerowe doświadczenie, które przedstawimy w dalszym ciągu tego paragrafu, przyjmujemy wartości możliwie małe. Dzięki temu uzyskamy wartości , co polepszy zgodność wyników komputerowej symulacji z rzeczywistością.
Z powyższego zapisu wynika także, że wielkość jest mianowana: . Jednostce tej nie nadajemy jednak nazwy „herc”, gdyż samo zjawisko rozpadu promieniotwórczego nie ma bezpośrednio charakteru okresowego. Dla izotopu stała rozpadu .
Połączenie wzorów (3.7) i (3.8) daje nam matematyczny „przepis” na śledzenie zmian liczebności próbki promieniotwórczej – w jednakowych (możliwie krótkich) odcinkach czasu liczebność ta zmienia się (maleje) o dane wzorem:
Należy jednak pamiętać, że we wzorze tym wielkość nie jest stała! Po każdym odcinku czasu jej wartość maleje, więc ubytki nie są jednakowe.
Przeprowadzimy „doświadczenie komputerowe” symulujące – w bardzo prostej wersji – rozpad wirtualnej próbki jąder promieniotwórczych zgodnie ze wzorem (3.9). Do tego doświadczenia przyjmiemy następujące założenia:
- Początkowa liczebność próbki .
- Będziemy obserwować liczebność próbki w umownych odstępach czasu .
- Przyjmiemy, że prawdopodobieństwo zajścia rozpadu pojedynczego jądra w jednosekundowym odstępie czasu wynosi 0,1. Oznacza to, że każde z jąder rozpada się w tym czasie z prawdopodobieństwem 10%.
- W celu uproszczenia symulacji przyjmiemy, że w każdym jednosekundowym odstępie czasu rozpada się dokładnie 10% próbki.
- Jeśli jądro nie ulegnie rozpadowi, to prawdopodobieństwo jego rozpadu w następnym odstępie czasu pozostaje stałe i nadal wynosi 10%.
W tabeli (il. 3.48) przedstawiono wynik takiego wirtualnego doświadczenia (dla uproszczenia podano jedynie kilka pierwszych wierszy tabeli), uzyskany w arkuszu kalkulacyjnym. W każdym wierszu pokazano czas, liczbę jąder, które nie uległy rozpadowi do tego czasu, oraz liczbę jąder , które ulegają rozpadowi w kolejnym odstępie czasu ; liczbę tę obliczono zgodnie ze wzorem (3.9):
Zwróćmy uwagę, że stanowi zawsze 10% aktualnej wartości (zaokrąglone do liczby całkowitej). W każdym kolejnym wierszu czas zostaje powiększony o , zaś liczebność zostaje pomniejszona o z poprzedniego wiersza.
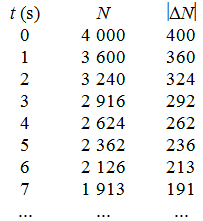
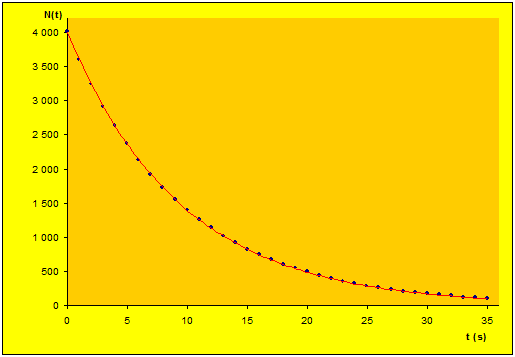
Na rysunku poniżej (il. 3.49) pokazano wykres uzyskanej zależności . Ma ona wszystkie cechy prawa rozpadu promieniotwórczego, o których wspominaliśmy wcześniej w tym rozdziale.
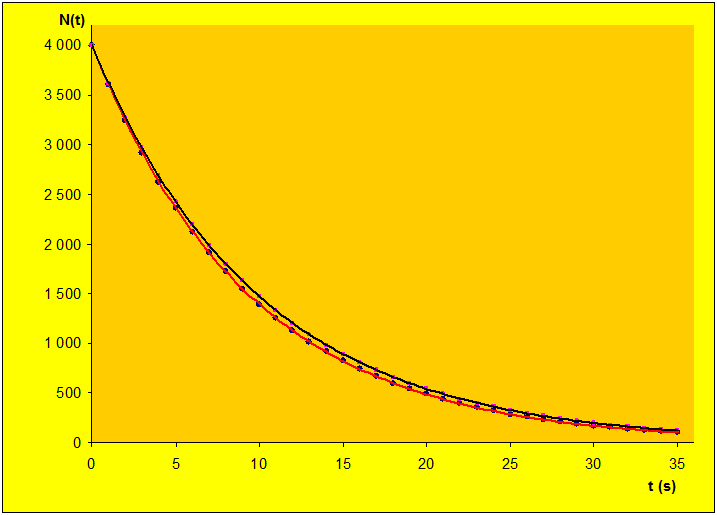
Na koniec pokażemy, że uzyskany w komputerowym doświadczeniu wykres jest w dobrym przybliżeniu zgodny z wykresem uzyskanym na podstawie wzoru (3.6):
w którym podstawiliśmy za iloraz . Na rysunku poniżej (il. 3.50) przedstawiono oba wykresy. Różnice między nimi wynikają z przybliżonego charakteru naszej symulacji komputerowej, w której przyjęliśmy jednosekundowe odstępy czasowe do określania kolejnych wartości liczebności próbki. Im krótszy czas zostałby w niej przyjęty, tym wykres czerwony (przybliżony) bardziej zbliżyłby się do wykresu czarnego (dokładnego).
Wyprowadzenie prawa rozpadu promieniotwórczego (materiał nadobowiązkowy)
Wyprowadzimy prawo rozpadu promieniotwórczego, wychodząc z ogólnych przesłanek i przyjmując całkowicie przypadkowy charakter promieniotwórczości jąder.
Przyjmijmy zatem, że rozpad promieniotwórczy danego jądra zachodzi zupełnie przypadkowo. Załóżmy także, że prawdopodobieństwo rozpadu jest stałe w czasie, tzn. zawsze po określonym odcinku czasu liczba jąder zanika jednakowo, np. po określonym czasie (tzw. okresie połowicznego zaniku) zanika połowa jąder, po czym znowu połowa itd.
Oznaczmy początkową liczbę jąder przez .
Po czasie będzie ich , czyli
po czasie : .
Po czasie będzie ich , czyli
po czasie : .
Po następnym odcinku czasu ich liczba jeszcze raz zmniejszy się o połowę, czyli łącznie po czasie będzie ich itd.
Widzimy, że po czasie ich liczba zmniejsza się według wzoru:
Uogólnijmy ten wzór. Najpierw zauważmy, że i dla dowolnego czasu mamy zależność:
Stąd
Otrzymaliśmy wzór – równoważny wzorowi (3.6) – określający prawo rozpadu promieniotwórczego wyrażone za pomocą okresu połowicznego zaniku .
Aby uzyskać wzór w postaci wykładniczej, należy przekształcić (3.11) w następujący sposób. Najpierw logarytmujemy obustronnie równość (3.11):
Stąd
Zatem
Oznaczmy wyrażenie w nawiasie przez :
( – tzw. stała rozpadu promieniotwórczego). Otrzymamy, że:
Funkcją odwrotną do logarytmu naturalnego jest funkcja wykładnicza, więc
Stąd ostateczna postać prawa rozpadu promieniotwórczego:
gdzie: – podstawa logarytmu naturalnego, – stała rozpadu; jej wartość jest charakterystyczna dla danego pierwiastka promieniotwórczego, – liczba jąder pierwotnych w chwili , – liczba jąder pierwotnych po czasie .
Pytania i problemy
- W podsumowaniu pod il. 3.44 podano orientacyjne skale czasowe, dogodne do przedstawiania zaniku czterech izotopów promieniotwórczych. Uzasadnij, że są one związane z prawdopodobieństwami zajścia przemiany dla tych izotopów. Skorzystaj z informacji w tekście bezpośrednio pod il. 3.44.
- Zilustruj graficznie fakt, że czas połowicznego zaniku nie musi być liczony od chwili zero. Wydrukuj wykres na il. 3.43 i zaznacz na nim odcinek odpowiadający liczony od początku obserwacji. Następnie pokaż, przykładowo, że od chwili osiągnięcia liczebności na poziomie 80% do chwili osiągnięcia 40% także mija .
- Uzupełnij wydrukowany wykres z il. 3.43 o linie obrazujące zanik próbki promieniotwórczej o czasie połowicznego zaniku dwa razy krótszym oraz dwa razy dłuższym niż pokazano na wykresie.
- W wykopaliskach pod Kaliszem znaleziono fragment drewnianej palisady. Poddano go datowaniu metodą radiowęglową i stwierdzono, że zawartość izotopu stanowi w nim ¾ zawartości oryginalnej. Oceń na tej podstawie, czy ta palisada mogła powstać za panowania pierwszych Piastów.
- Przedstaw, w możliwe ogólnym ujęciu, pojęcie stałej rozpadu promieniotwórczego .
- Wydrukuj wykres 5. (il. 3.49) i zaznacz na nim odcinek odpowiadający , liczony od początku obserwacji. Następnie pokaż, że kolejnym odcinkom odpowiadają połówkowe zaniki liczebności próbki.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
