Obecnie mamy już wiedzę wystarczającą do tego, aby zrozumieć w jaki sposób można opisać oddziaływanie magnetyczne na gruncie prawa Coulomba, niezmienniczości ładunku elektrycznego i szczególnej teorii względności.

Rozważmy szczególny przypadek oddziaływania magnetycznego prostoliniowego przewodnika z prądem na poruszający się pojedynczy ładunek. Może to być np. elektron w sytuacji wcześniej opisanej w rozdziale 3.3. Siła Lorentza i wektor indukcji pola magnetycznego (il. 3.14; patrz również przykład w rozdziale 3.5. Prawo Ampère'a). Przyjrzyjmy się jeszcze raz bliżej tej sytuacji (il. 10.9). Ładunek $q$ poruszający się równolegle do przewodnika z prądem doznaje działania siły Lorentza ${\overrightarrow{F}}_B$, która jest zwrócona w tym przypadku w stronę przewodnika. Należy zauważyć, że na ładunek nie działa żadna siła elektrostatyczna, ponieważ przewód z prądem elektrycznym nie jest naładowany. Całkowity ładunek elektronów jest dokładnie skompensowany przez dodatni ładunek jonów sieci krystalicznej przewodnika. W przewodniku jest tyle samo ładunków ujemnych – elektronów, co ładunków dodatnich – jonów. Tak sytuacja wygląda w układzie odniesienia $U$, w którym przewodnik spoczywa, a ładunek $q$ się porusza z prędkością $v$, równą prędkości unoszenia elektronów w przewodniku $\text{(}v=u_D\text{)}$. Widzimy, że w tym układzie na ładunek działa siła prostopadła do prędkości ładunku. Stwierdzamy, że siła ta jest siłą oddziaływania pola magnetycznego o indukcji $\overrightarrow{B}$ na poruszający się ładunek.

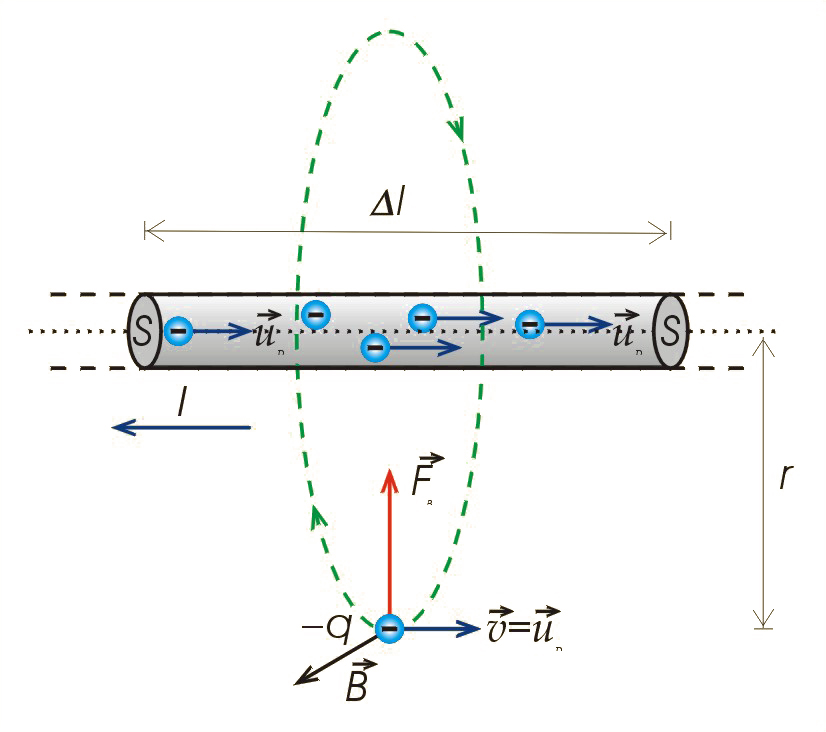
Spójrzmy teraz na tę samą sytuację z punktu widzenia układu $U\text{'}$, poruszającego się z prędkością równą prędkości ładunku. W tym układzie ładunek spoczywa, więc – zgodnie ze wzorem na siłę Lorentza (3.5) – siła magnetyczna nie występuje. Czy to znaczy, że dla obserwatora ruchomego (układ $U\text{'}$) ładunek nie będzie przyciągany do przewodnika z prądem? Oczywiście, byłby to absurd, gdyż ładunek jest realnie przyciągany do przewodnika i dlatego będzie się do niego zbliżał w każdym układzie odniesienia (przecież nie zatrzymamy zbliżania się ładunku do przewodnika tylko przez to, że inaczej będziemy na niego patrzeć!).

W takim razie, skoro w układzie $U\text{'}$ siła przyciągająca nie znika, a nie jest to siła Lorentza, to jak ją wytłumaczyć? Skąd się ona bierze? I tu przychodzi nam z pomocą teoria względności, z której dowiedzieliśmy się (patrz rozdz. Względność wymiarów przestrzennych), że przedmioty ruchome doznają skrócenia swoich wymiarów wzdłuż kierunku ich ruchu – tzw. skrócenia Lorentza. Zatem odległości wzajemne jonów dodatnich sieci krystalicznej przewodnika ulegają skróceniu, a odległości elektronów – nie (ponieważ w układzie $U\text{'}$ elektrony nie mają wypadkowej prędkości wzdłuż przewodnika). Wobec tego w układzie $U\text{'}$ ładunki dodatnie jonów są rozłożone w objętości przewodnika gęściej niż ładunki ujemne elektronów. O ile w układzie $U$ ładunki elektronów i jonów dokładnie się kompensują, to w układzie $U\text{'}$ przewodnik jest naładowany dodatnio i występuje pole elektryczne, które przyciąga ładunek znajdujący się na zewnątrz przewodnika (il. 10.10). Pokażemy niżej, że tę siłę oddziaływania kulombowskiego można wyrazić wzorem dokładnie takim, jak wzór na siłę Lorentza.

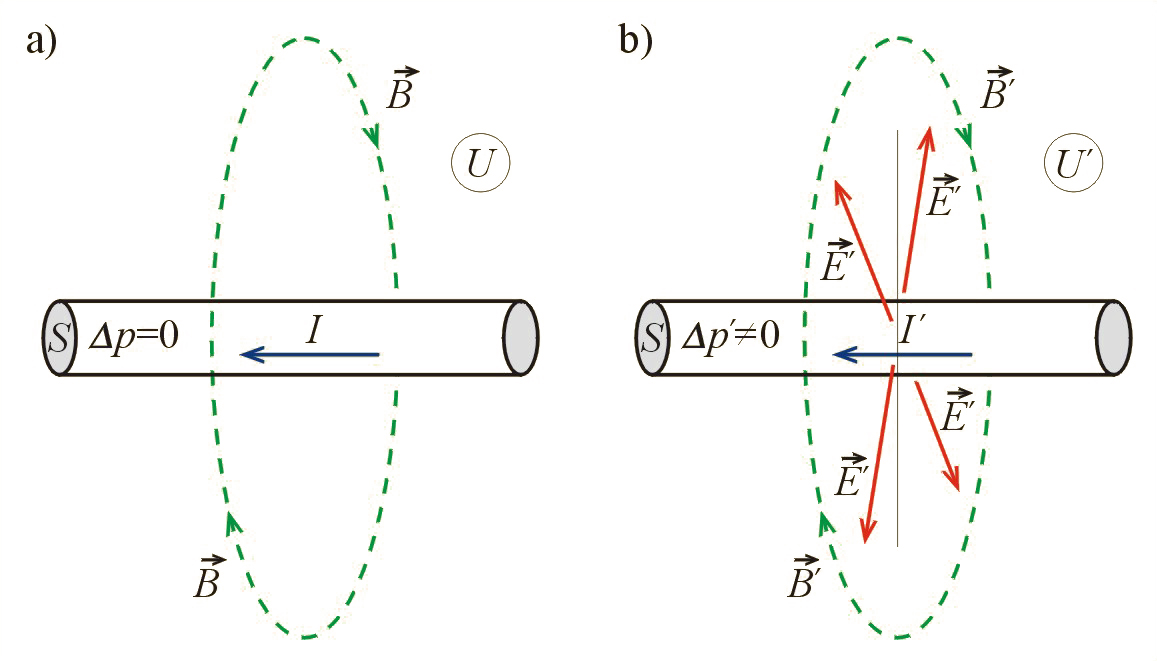
Siła oddziaływania magnetycznego jest zatem wynikiem praw teorii względności (relatywistycznego skrócenia długości), prawa Coulomba (czyli występowania siły elektrycznej w układzie $U\text{'}$) oraz prawa niezmienniczości ładunku elektrycznego. O zmianie gęstości ładunków jonów na skutek skrócenia długości wolno nam mówić pod warunkiem, że w nowym układzie odniesienia $U\text{'}$ wartość ładunku się nie zmienia – czyli ładunek jest niezmienniczy, niezależny od prędkości.

Prawo niezmienniczości ładunku elektrycznego jest potwierdzone doświadczalnie. Oto przykład. Różne cząstki elementarne (w tym protony i elektrony) są przyspieszane w akceleratorach od prędkości bliskich zeru do prędkości bliskich $c$. Tryb pracy wielu typów akceleratorów, od prostych cyklotronów po współczesne narzędzia takie jak LHC (tzw. Wielki Zderzacz Hadronów Genewie), zależy m. in. od wartości ładunku przyspieszanych cząstek. W żadnym doświadczeniu nie stwierdzono, by ładunek określonej cząstki zmieniał się w trakcie jej przyspieszania. Gdyby tak było, to większość akceleratorów nie działałaby w sposób oczekiwany przez projektantów i fizyków. Każda sekunda pracy tych akceleratorów potwierdza, że wartość ładunku nie zależy od prędkości.

Opisane powyżej relatywistyczne uzasadnienie siły Lorentza jest uzasadnieniem jakościowym. Obecnie pokażemy, że przedstawione rozumowanie da się uzasadnić ilościowo. W tym celu rozważymy najpierw sytuację w układzie $U$. Siła działająca na ruchomy ładunek $q$ w polu magnetycznym prostoliniowego przewodnika z prądem dana jest za pomocą wzoru (3.26) z przykładu (rozdz. 3.5. Prawo Ampère'a) i wynosi:

(W celu uproszczenia rachunków przyjęliśmy, tak samo jak w przykładzie 5, że ładunek $q$ ma prędkość $v=u_D$.)

Przyjmiemy, że ładunki w przewodniku są skompensowane, tzn. że gęstość ładunków dodatnich (jonów) jest równa gęstości ładunków ujemnych (elektronów), co symbolicznie zapisujemy: ${\rho }_{+}={\rho }_{-}=\rho$, czyli ${\rho }_{+}-{\rho }_{-}=0$

Przejdźmy teraz do układu $U\text{'}$ poruszającego się z prędkością $v$ wraz z ładunkiem $q$. W tym układzie ładunek $q$ spoczywa. Natomiast gęstość ładunku jonów dodatnich wynosi ${\rho }_{+}^{\text{'}}=\frac{\Delta q_{+}}{\Delta V\text{'}}=\frac{\Delta q_{+}}{S\Delta l\text{'}}$ (przyjęliśmy tu, zgodnie z zasadą niezmienniczości ładunku, że $\Delta q\text{'}=\Delta q$). Zgodnie ze wzorem (10.12) na skrócenie długości, mamy:

Zatem

Skoro $\frac{\Delta q_{+}}{S\Delta l}=\frac{\Delta q_{+}}{\Delta V}=\rho$, to:

Widzimy, że gęstość ładunku dodatniego ${\rho }_{+}^{\text{'}}$ jest większa niż w układzie $U$, gdzie wynosiła ${\rho }_{+}=\rho$.

W układzie $U\text{'}$ prędkość unoszenia ładunków ujemnych – elektronów – jest równa zeru, a gęstość ładunku ujemnego ${\rho }_{-}^{\text{'}}$. Natomiast w układzie $U$ elektrony mają prędkość unoszenia równą $v$, a gęstość ich ładunku ujemnego wynosi $\rho$. Zatem dla ładunku ujemnego elektronów obowiązuje taki sam wzór jak (10.34), ale zapisany w następujący sposób:

Widzimy, że ${\rho }_{-}^{\text{'}}<\rho$ – gęstość ładunku ujemnego elektronów jest mniejsza niż w układzie $U$.

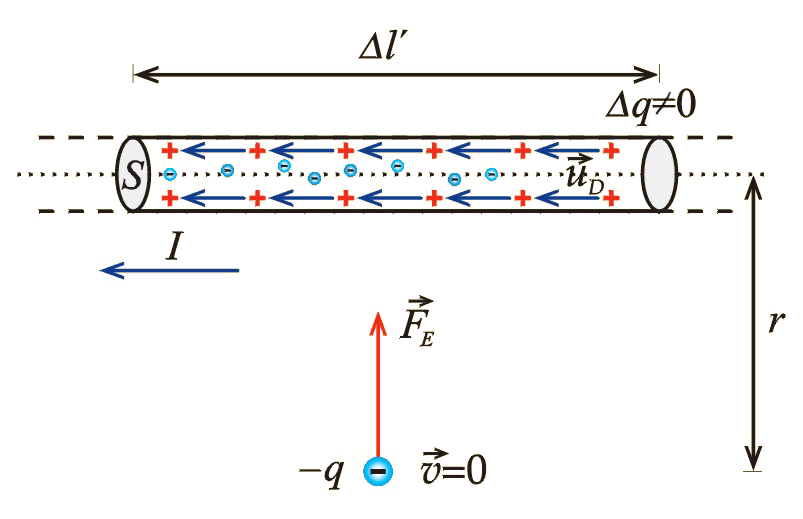
W układzie $U\text{'}$ przewodnik jest naładowany dodatnio ładunkiem o gęstości ${\Delta \rho \text{'}=\rho }_{+}^{\text{'}}-{\rho }_{-}^{\text{'}}$. Korzystając ze wzorów (10.34) i (10.35), otrzymamy:

czyli

Zatem na ładunek $q$ będzie działać siła elektrostatyczna (il. 10.11) o wartości:

pochodząca od pola $\overrightarrow{E}\text{'}$ o symetrii cylindrycznej, jak na il. 10.10b, wytworzonego przez naładowany przewodnik ładunkiem o gęstości $\Delta \rho \text{'}$.

Wartość natężenia pola wytworzonego przez prostoliniowy przewodnik równomiernie naładowany ładunkiem o gęstości $\Delta \rho \text{'}$ wynosi:

(wzór ten podajemy bez wyprowadzenia; zainteresowani wyprowadzeniem uczniowie bez trudu znajdą je w Internecie, np. pod hasłem „prawo Gaussa”). Zatem:

Po podstawieniu $\Delta \rho \text{'}$ ze wzoru (10.36) otrzymamy:

Z przykładu – wzór (3.24) – wiemy, że $c^2=\frac{1}{{\epsilon }_0{\mu }_0}$, więc ${\mu }_0=\frac{1}{{\epsilon }_0{c}^2}$. Jeżeli podstawimy to do wzoru (10.39), otrzymamy następujący wzór na siłę $F_E^{\text{'}}$:

Widzimy, że siła $F_E^{\text{'}}$ jest równa sile Lorentza $F_B$ określonej za pomocą wzoru (10.32):

z dokładnością do wartości pierwiastka występującego w mianowniku. Rzeczywiście,

więc wartości tych sił są prawie identyczne z obu punktów widzenia, a dla małych prędkości są równe. Możemy powiedzieć, że przynajmniej w przypadku małych prędkości widać, iż magnetyzm i elektryczność są po prostu „dwoma sposobami patrzenia na tę samą rzecz”.

Wartość siły $F_E^{\text{'}}$ określona za pomocą wzoru (10.40) to wartość, jaką uzyskałby w wyniku pomiaru obserwator ruchomy – poruszający się wraz z ładunkiem. Natomiast my mierzymy tę siłę w układzie nieruchomym. Powinno się zatem wziąć pod uwagę fakt, że przy przejściu z jednego układu do drugiego siły również podlegają transformacji relatywistycznej. Siła $F_B$ okaże się wtedy dokładnie równa sile Lorentza, dla dowolnych prędkości.

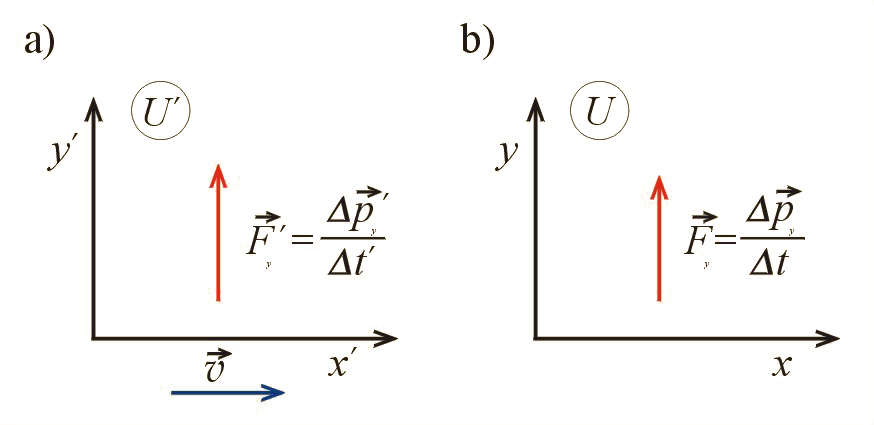
Przekonamy się, że te „dwa sposoby patrzenia na to, co się dzieje naprawdę”, dają ten sam wynik fizyczny dla dowolnej prędkości.

Zapytajmy, jak transformuje się siła poprzeczna $F_y^{\text{'}}$ przy przejściu z układu $U\text{'}$ do układu $U$. Na il. 10.12 pokazano siły poprzeczne do kierunku ruchu układu – ${\overrightarrow{F}}_y^{\text{'}}$ mierzoną w układzie $U\text{'}$ i ${\overrightarrow{F}}_y$ mierzoną w układzie $U$. Siła poprzeczna w układzie $U\text{'}$ jest równa:

w układzie $U$ zaś:

Podzielimy stronami powyższe dwie równości. Otrzymamy:

W kierunku poprzecznym przyrosty pędu w obu układach będą jednakowe (bo $y\text{'}=y$, zaś początkowa prędkość elektronu w kierunku $y$ wynosi zero), więc $\frac{\Delta p_y^{\text{'}}}{\Delta p_y}=1$. Natomiast upływ czasu nie będzie jednakowy (wystąpi tzw. dylatacja czasu). Z nauki teorii względności wiemy (patrz rozdz. Dylatacja czasu), że:

zatem, zgodnie z (10.44), otrzymamy:

Widzimy więc, że związek między tą samą siłą poprzeczną mierzoną w jednym układzie i drugim jest dokładnie taki sam, jak związek (10.41) między siłą elektryczną w układzie $U\text{'}$ a magnetyczną w układzie $U$, dla dowolnych prędkości, co właśnie mieliśmy wykazać.

Opisana tu współzależność pól elektrycznego i magnetycznego pokazuje kluczową rolę szczególnej teorii względności w zrozumieniu i opisie zjawisk elektromagnetycznych. Są one relatywistyczne już na poziomie najprostszego możliwego ujęcia. Pod tym względem różnią się od mechaniki, która ma swe ujęcie nierelatywistyczne, połączone zasadą korespondencji z jej ujęciem relatywistycznym.

Innym, ciekawym ujęciem tej różnicy jest fakt, iż relatywistyczny charakter zjawisk elektromagnetycznych objawia się mimo nierelatywistycznych (z punktu widzenia mechaniki!) prędkości unoszenia ładunków w przewodzie z prądem. Tak więc nie jest zbyt precyzyjne stwierdzenie, że obserwowanie efektów rodem ze szczególnej teorii względności jest możliwe tylko przy prędkościach obiektów (układów odniesienia) porównywalnych z  $c$ – prędkości dryfu elektronów w przewodzie są rzędu milimetrów na sekundę.