Celem doświadczenia jest doświadczalne sprawdzenie wzoru soczewkowego $\frac{1}{f}=\frac{1}{x}+\frac{1}{y}$ oraz wyznaczenie ogniskowej (zdolności skupiającej) użytej w nim soczewki.

Wartość ogniskowej soczewki możemy w przybliżeniu ocenić, mierząc odległość od soczewki do obrazu jakiegoś odległego przedmiotu (w słoneczny dzień możemy skupić za pomocą soczewki promienie słońca w ognisku, w dzień pochmurny wytwarzamy na kartce papieru obraz na przykład żarówki lampy wiszącej przy suficie). W naszym doświadczeniu użyjemy soczewki skupiającej o ogniskowej wynoszącej około 30 cm i wyznaczymy dokładną wartość tej ogniskowej.

Przebieg pomiarów

Na ławie optycznej ustawiamy żaróweczkę i ekran; między nimi umieszczamy soczewkę w odległości $x$ o 4–5 cm większej niż ogniskowa soczewki (jak na il. 8.56). Zmieniając położenie ekranu, doprowadzamy do uzyskania na nim ostrego obrazu żaróweczki. Mierzymy odległości $x$ i $y$. Zwiększamy $x$ (początkowo o 2–3 cm, w dalszych pomiarach o 4–5 cm), oddalając soczewkę od żaróweczki, korygujemy położenie ekranu i mierzymy nowe wartości $x$ i $y$.

Czynności te powtarzamy wielokrotnie, np. 10 razy (do uzyskania odległości $x$ rzędu $3f$), notując za każdym razem wyniki pomiarów odległości $x$ i $y$. Zwracamy przy tym uwagę na zakres wartości $y$, w jakim ustawienie ekranu pozwala uznać, że otrzymany obraz jest ostry. Jeśli dla większości pomiarów zakres ten okaże się być większy od podziałki na ławie optycznej (w naszym doświadczeniu to 1 cm), to wpłynie on na naszą ocenę niepewności $\Delta y$, z jaką wyznaczamy odległość $y$.

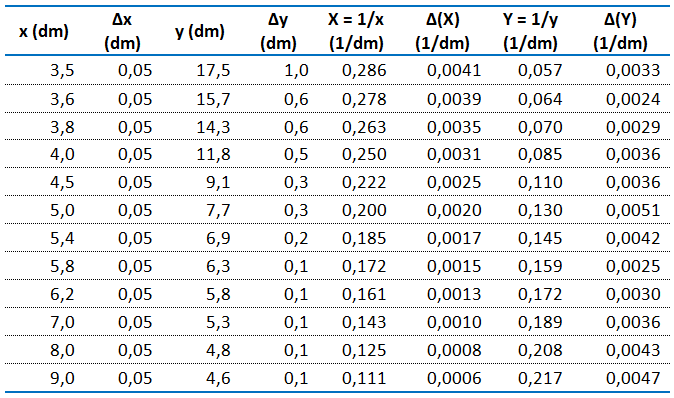
Wyniki pomiarów wpisujemy do uprzednio przygotowanej tabelki pomiarów (il. 8.57).

Niepewności pomiarowe wielkości prostych i wielkości złożonych

W trakcie pomiarów odległość $x$ (zmienna niezależna w naszym doświadczeniu) była ustalana i odczytywana z dokładnością taką, na jaką pozwalała podziałka oraz inne czynniki, jak rozmiar żaróweczki i soczewki. Dokładność tę oszacowaliśmy na 0,1 dm, stąd maksymalna niepewność pomiarowa $\Delta x=\mathrm{0,05}\text{dm}$ (0,5 cm), jednakowa dla wszystkich pomiarów.

Inaczej ma się sprawa ze zmienną zależną – odległością $y$. Jej odczyt jest obarczony taką samą niepewnością co ustalanie i odczyt zmiennej $x$. Jednak przy ustalaniu położenia ekranu, w którym powstawał na nim ostry obraz, pojawiła się niepewność o większym rozmiarze. Wynika ona z efektu zbliżonego do tzw. głębi ostrości, znanej z fotografii. Okazało się, że im większa odległość $y$, tym trudniej było ustalić „właściwe” położenie ekranu. Zakres położeń, przy których można było uznać, że obraz jest ostry, wynosił ok. 0,2 dm dla wartości $y$ poniżej $2f$; powyżej tej wartości zakres ten wzrastał aż do 2 dm. Te spostrzeżenia, odnotowane w trakcie pomiarów, są podstawą do oszacowania $\Delta y$, różnych dla poszczególnych pomiarów, zapisanych w tabeli na il. 8.57.

Niepewności odwrotności mierzonych zmiennych, $\Delta X$ i  $\Delta Y$, obliczone zostały zgodnie ze wzorem dla niepewności odwrotności, wyprowadzonym w rozdz. 1.7 Ocena niepewności pomiarowych, tom II:

Wykres zależności $y$ od $x$

Korzystając z tabeli, tworzymy wykres zależności $y$ od $x$, przedstawiony na il. 8.58a. Oczekiwane ułożenie punktów pomiarowych przedstawia wykres na il. 8.58b; jest on fragmentem wykresu z il. 8.54, odpowiadającym $f>0$ oraz $x>f$.

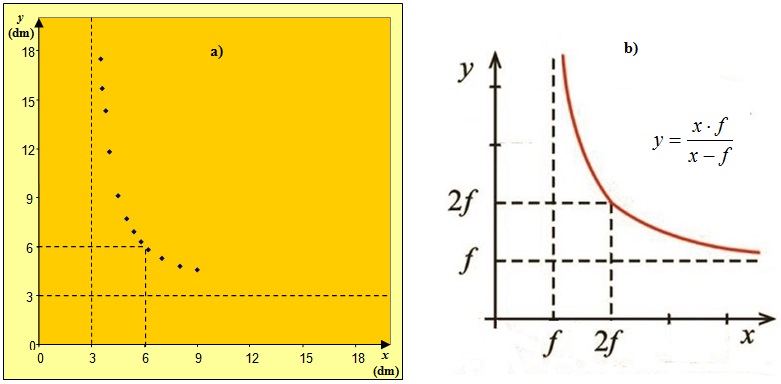
Cieszymy się, gdyż ułożenie punktów na naszym wykresie jest takie, jak na wykresie teoretycznym. Punkty pomiarowe prawidłowo oddają zachowania asymptotyczne krzywej wzorcowej: gdy $x$, malejąc, dąży do $f$, to $y$ gwałtownie rośnie; nieco mniej widoczne (ze względu na dziedzinę doświadczenia) jest dążenie $y$ do $f$ przy wzroście $x$. Wyobrażona linia krzywa przechodząca możliwie blisko punktów doświadczalnych zawiera punkt $\text{(}2f;2f\text{)}$. Świadczy to o jakościowej zgodności z teorią uzyskanych przez nas wyników.

Stwierdzamy także, że żaden z punktów nie odstaje w sposób istotny od tendencji wskazanych przez pozostałe. To z kolei świadczy o tym, że nie popełniono w doświadczeniu żadnej pomyłki (błędu grubego).

Przekształcenie danych pomiarowych

Musimy się upewnić, czy nasz wykres rzeczywiście odpowiada krzywej teoretycznej wynikającej ze wzoru soczewkowego (8.52). W tym celu tworzymy wykres w układzie współrzędnych $X=\frac{1}{x}$ i $Y=\frac{1}{y}$.

Jest to znana nam procedura „prostowania” zależności nieliniowej.Wygodnie jest też operować zdolnością skupiającą soczewki $\Phi =\frac{1}{f}$, pamiętając przy tym, że odległości w tym doświadczeniu wyrażamy w decymetrach. Wzór soczewkowy, przy takim podstawieniu zmiennych, przyjmie postać:

Jest to zależność liniowa o postaci $Y=aX+b$, w której współczynnik kierunkowy $a=-1$. Współczynnik wolny $b=\Phi$, pozwoli wyznaczyć ogniskową soczewki: $f=\frac{1}{b}$. Oczekujemy, że przekształcone punkty pomiarowe ułożą się w pobliżu takiej właśnie prostej. Dane z tabeli na il. 8.57 wraz z prostokątami niepewności pomiarowej oraz prostą optymalną pokazano na il. 8.59. Skalę wykresu dobrano w taki sposób, by spodziewane punkty przecięcia prostej optymalnej z osiami (okolice $X=\frac{1}{3}\text{1/dm}$ i  $Y=\frac{1}{3}\text{1/dm}$) widniały na wykresie.

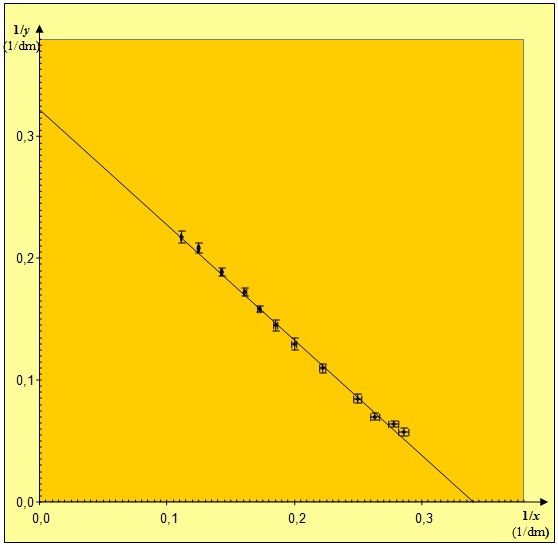
Stwierdzamy, że prosta optymalna przechodzi przez wszystkie prostokąty niepewności pomiarowej. Jest to potwierdzenie liniowej zależności między $Y$ i  $X$, czyli zależności między $y$ i  $x$ zgodnej ze wzorem soczewkowym.

Wyniki pomiarów

Z wykresu odczytujemy bezpośrednio, w punkcie przecięcia prostej optymalnej z osią $Y$, wartość odwrotności ogniskowej, czyli zdolności skupiającej oraz ogniskowej soczewki:

Nie dysponujemy żadną wartością wzorcową ogniskowej $f$, której uzyskanie warunkowałoby stwierdzenie powodzenia eksperymentu. Producent użytej soczewki nie umieścił na niej żadnej informacji o jej zdolności skupiającej. Oszacowana przez nas ogniskowa, na potrzeby wstępnej orientacji w doświadczeniu, równa 3 dm, nie spełnia roli takiego wzorca. Dlatego też oszacujemy niepewność $\Delta f$ (zgodnie z zasadą, że każdy wynik pomiaru winien zawierać choćby oszacowanie niepewności pomiarowej), choć nie będziemy porównywali $f$ z jakąkolwiek inną ogniskową.

Po podzieleniu wartości punktu przecięcia prostej z osią rzędnych przez wartość punktu przecięcia prostej z osią odciętych, otrzymujemy nachylenie prostej optymalnej:

Inaczej niż w przypadku ogniskowej, dla współczynnika kierunkowego $a$ mamy wartość wzorcową $a_w=-1$. Uzyskana wartość $a$ jest bliska wzorcowej: procentowe odstępstwo od wartości wzorcowej wynosi około 6%. Nie możemy jednak orzec o zgodności wyniku doświadczenia z oczekiwaniami bez oszacowania niepewności pomiarowej $\Delta a$.

Niepewności pomiarowe wyników

Zastosujemy postępowanie, które już kilkakrotnie pozwalało nam oszacować niepewność pomiarową współczynnika kierunkowego prostej optymalnej, np. w doświadczeniach „AkceleracjaBis” (rozdz. 4.9 Doświadczenie „Akceleracja BIS”, tom II), „Izobara” (rozdz. 6.5 Doświadczenie „Izobara”, tom II), „Ohm” (rozdz. 2.4. Doświadczenie „Ohm”) czy „Snellius” (rozdz. 8.2. Doświadczenie „Snellius”). Polega ono na naniesieniu dwóch prostych skrajnych, przechodzących przez wszystkie prostokąty niepewności pomiarowej. Przebieg prostych skrajnych przedstawiono na wykresie na il. 8.60.

Prosta niebieska ma największą dopuszczalną stromiznę (co do wartości bezwzględnej) i przecina oś $Y$ w największej dopuszczalnej współrzędnej. Wyznacza ona więc $a_{\text{max}}$ (co do wartości bezwzględnej) oraz ${\Phi }_{\text{max}}$. Analogicznie, prosta czerwona wyznacza $a_{\text{min}}$ (co do wartości bezwzględnej) oraz ${\Phi }_{\text{min}}$. Na wykresie zaznaczamy też dwa punkty $X_1$ i $X_2$. Są to punkty przecięcia prostych skrajnych z osią $X$; posłużą one, wraz z punktami ${\Phi }_{\text{max}}$ i ${\Phi }_{\text{min}}$, do obliczenia nachyleń tych prostych.

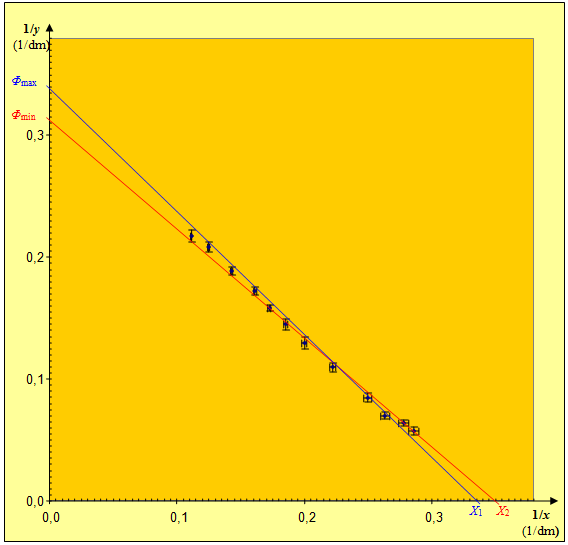
Odczytujemy z wykresu na il. 8.60 odpowiednie współrzędne:

Na tej podstawie obliczamy:

Jako niepewność pomiarową $\Delta a$ przyjmujemy połowę (wartości bezwzględnej) różnicy między $a_{\text{max}}$ i $a_{\text{min}}$:

Tak więc współczynnik kierunkowy (nachylenie) prostej optymalnej wynosi:

Wynik ten jest zgodny z hipotezą, że $a=a_w=-1$. Potwierdza to zgodność wyników pomiarów ze wzorem soczewkowym.

Jako niepewność pomiarową $\Delta \Phi$ przyjmujemy połowę różnicy pomiędzy ${\Phi }_{\text{max}}$ i ${\Phi }_{\text{min}}$:

Tak więc zdolność skupiająca soczewki wynosi:

Względna niepewność wyznaczenia ogniskowej $f$ jest taka sama jak względna niepewność wyznaczenia zdolności skupiającej $\Phi$ (gdyż wielkości te są swymi odwrotnościami):

Ostatecznie więc ogniskowa użytej soczewki wynosi:

Podsumowanie

W doświadczeniu zbadano zależność odległości $y$ między obrazem a soczewką od odległości $x$ przedmiotu od tej soczewki. Okazało się, że zależność ta jest zgodna ze wzorem soczewkowym. Za taką tezą przemawiają następujące argumenty:

• ułożenie punktów pomiarowych na wykresie $y\text{(}x\text{)}$ jest bardzo podobne do tej samej zależności, wynikającej ze wzoru soczewkowego;
• ułożenie punktów na wykresie $Y\text{(}X\text{)}$, gdzie $Y$ i $X$ są odwrotnościami, odpowiednio $y$ i $x$, ma charakter liniowy, zgodnie ze wzorem soczewkowym;
• prosta optymalna przybliżająca zależność $Y\text{(}X\text{)}$ przechodzi przez wszystkie punkty niepewności pomiarowej;
• wartość współczynnika kierunkowego zależności $Y\text{(}X\text{)}$ $a=-\mathrm{0,94}\pm \mathrm{0,06}$, jest ona zgodna z oczekiwaną wartością wzorcową $a_w=-1$.

Wyznaczono ogniskową użytej soczewki $f=\mathrm{3,12}\pm \mathrm{0,13}\text{dm}$, z dokładnością względną 4,1%.

Pytania i problemy

W ramach uzupełnienia doświadczenia z soczewką skupiającą przeprowadź następujące obserwacje i pomiary:

1. Wykorzystaj ławę optyczną jak na il. 8.56, z soczewką o znanej ogniskowej $f$. Umieść ekran w odległości $d$ większej niż $4f$ (np. $6f$) od żarówki. Między ekranem a żarówką umieść soczewkę; przesuwając ją po ławie optycznej, znajdź takie dwa jej położenia, w których uzyskasz ostry obraz żarówki na ekranie. Przekonaj się, że więcej takich położeń nie ma.

   Zmierz i zapisz odległości $x_1$ i $y_1$ dla jednego z tych położeń soczewki oraz odległości $x_2$ i $y_2$ dla drugiego położenia; oszacuj ich niepewności pomiarowe. Uwzględnij tzw. głębię ostrości zarówno przy pomiarach $x$ i $y$, jak i przy dyskusji niepewności pomiarowych. Zwróć uwagę na rozmiary obrazu w każdym z tych przypadków. Uzupełnij opis swojego doświadczenia o wnioski, zgodnie z poniższymi poleceniami.

   1. Wskaż prawidłowość w obrębie par odległości $x_1$ i $y_2$ oraz $x_2$ i $y_1$. Jaki związek ma ta prawidłowość z zasadą „odwracalności biegu promieni świetlnych”?
   2. Wskaż, w którym z tych dwóch położeń soczewka spełnia rolę zbliżoną do obiektywu aparatu fotograficznego, a w którym – do obiektywu rzutnika slajdów. Do którego z tych przypadków zaliczyłbyś rolę spełnianą przez soczewkę w oku ludzkim?
2. Przeprowadź obserwację z punktu 1., ale zmniejsz odległość $d$ do wartości mniejszej niż $4\cdot f$ (np. $3\cdot f$). Przekonaj się, że nie jest możliwe znalezienie takiego położenia soczewki, w którym uzyskuje się ostry obraz żarówki na ekranie. Uzupełnij opis swojego doświadczenia o rozważania teoretyczne, zgodnie z poniższymi poleceniami.
   1. Uzasadnij, że poniższy układ równań opisuje przebieg obserwacji z punktu 1.
      $$\{\begin{array}{c}x+y=d\\ \frac{1}{x}+\frac{1}{y}=\frac{1}{f}\end{array}$$
   2. Przekształć ten układ równań w taki sposób, by uzyskać z niego jedno równanie na odległość $x$. Przeanalizuj warunek rozwiązywalności tego równania i uzasadnij różnicę między efektem uzyskanym w punkcie 1. a brakiem efektu w punkcie 2.
   3. Przeanalizuj rozwiązanie równania uzyskanego w poleceniu 2b) i wyjaśnij, dlaczego w doświadczeniu z punktu 1. uzyskałeś tylko dwa położenia, w których na ekranie powstał ostry obraz żarówki.
3. Wykonaj sprawozdanie z przeprowadzonego doświadczenia według standardowego wzorca.