4.2. Prawo indukcji Faradaya
Faraday, zanim sformułował prawo indukcji elektromagnetycznej, wykonał wiele doświadczeń. Omówimy tu niektóre z nich.
Na il. 4.5 przedstawiony jest układ doświadczalny zbudowany specjalnie w celu wykazania, że przyczyną powstania prądu indukcyjnego w obwodzie jest zmienny strumień pola magnetycznego, niezależnie od tego, czy pole to pochodzi od magnesu stałego, czy od innego obwodu z prądem. Dwie pętle przewodnika umieszczamy blisko siebie. Jedna pętla jest podłączona – poprzez przełącznik i opornik – do źródła prądu stałego, druga zaś do galwanometru. Podczas włączania i wyłączania przełącznika w jednym obwodzie, w drugim wychyla się wskazówka galwanometru, świadcząc o pojawieniu się prądu indukcyjnego. Także gwałtowna zmiana jej położenia – odsunięcie bądź przysunięcie, przemieszczenie w płaszczyźnie pętli, a także obrót – indukuje prąd. Z kolei gdy przez jedną z pętli płynie stały prąd i obie pętle są w spoczynku, w drugiej nie indukuje się żaden prąd.
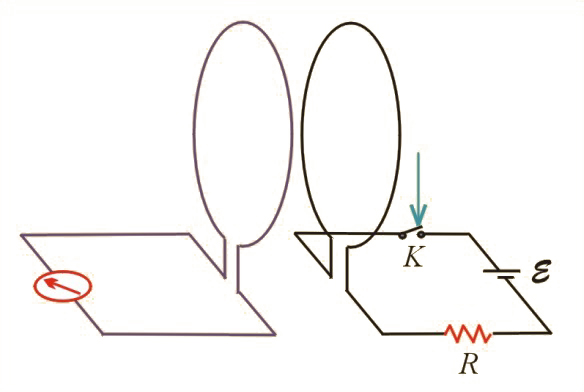
Spróbujemy teraz wyciągnąć ogólny wniosek z tych doświadczeń. Najpierw zauważmy, że obwód z galwanometrem może reagować na zmiany w jego otoczeniu jedynie za pośrednictwem pola magnetycznego.
W obwodzie nie powstaje żadna siła elektromotoryczna i nie płynie żaden prąd indukcyjny, gdy zewnętrzne pole magnetyczne jest stałe (np. w przypadku przepływu stałego prądu w drugim obwodzie i nieruchomych obydwu obwodach).
Natomiast gdy przez obwód przenika zmienne pole magnetyczne pochodzące od zmiennego prądu w drugim obwodzie (prąd się zmienia przy włączaniu i wyłączeniu przełącznika), to w obwodzie powstaje siła elektromotoryczna i płynie prąd indukcyjny.
Ponadto siła elektromotoryczna w obwodzie może powstać nawet przy stałym zewnętrznym polu magnetycznym. Niech zmienia się przestrzenne położenie obwodu – wtedy zmianie ulegać może efektywne pole magnetyczne przechodzące przez przekrój tego obwodu. Mówimy, że zmienia się strumień pola magnetycznego.
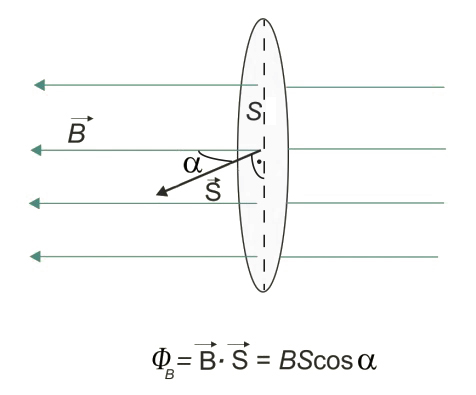
Strumień pola magnetycznego jest wielkością fizyczną, którą definiujemy jako iloczyn skalarny wektorów i :
gdzie jest wektorem prostopadłym do powierzchni, którego wartość równa się wartości pola powierzchni , a jest kątem między wektorem i (il. 4.6).
Jednostką strumienia magnetycznego jest weber . Jeden weber jest strumieniem indukcji magnetycznej o wartości 1 tesli przecinającej pod kątem prostym powierzchnię 1 metra kwadratowego. .
Widzimy, że w obwodzie, w którym nie ma ogniwa, indukuje się prąd dlatego, że zmienia się strumień pola magnetycznego przenikającego obwód. Wniosek ogólny z tych doświadczeń jest następujący:
Doświadczenie pokazowe
Do przeprowadzenia doświadczenia potrzebne są dwie zwojnice (cewki) o różnych średnicach, rdzeń żelazny dopasowany do mniejszej zwojnicy, magnes sztabkowy, mikroamperomierz (o zakresie ok. 1 mA) z zerem pośrodku oraz akumulator lub inne niskonapięciowe źródło prądu stałego.
- Większą cewkę podłączamy dwoma przewodami do mikroamperomierza. Gwałtownym ruchem wkładamy do niej sztabkę magnesu (il. 4.8a). W taki sam sposób wyciągamy sztabkę z cewki. Zauważamy, że podczas wkładania i wyjmowania magnesu wskazówka amperomierza wychyla się (raz w jedną stronę, raz w drugą) – w cewce indukuje się prąd. Odwrócenie magnesu i wkładanie go do cewki przeciwnym biegunem powoduje wychylenie amperomierza w przeciwnym kierunku. W czasie, gdy magnes znajduje się wewnątrz cewki i jest nieruchomy, amperomierz nie wychyla się – przez cewkę nie przepływa prąd.
- Mniejszą cewkę podłączamy do akumulatora (il. 4.8b). Cewka z prądem staje się magnesem. Wkładamy ją gwałtownie do większej cewki. Amperomierz zachowuje się podobnie jak poprzednio, czego należało się spodziewać, gdyż mniejsza cewka z prądem wytwarza pole magnetyczne podobne do pola sztabki.
- Do mniejszej cewki wstawiamy rdzeń żelazny i po podłączeniu jej do akumulatora wkładamy ją gwałtownie do cewki dużej. Przekonujemy
się, że wychylenia amperomierza są teraz znacznie większe. Spodziewaliśmy się tego, gdyż rdzeń powoduje znaczne wzmocnienie
pola magnetycznego. Silniejszy zmienny strumień pola magnetycznego przepływający przez cewkę większą indukuje w niej silniejszy
prąd, co wykazuje amperomierz.
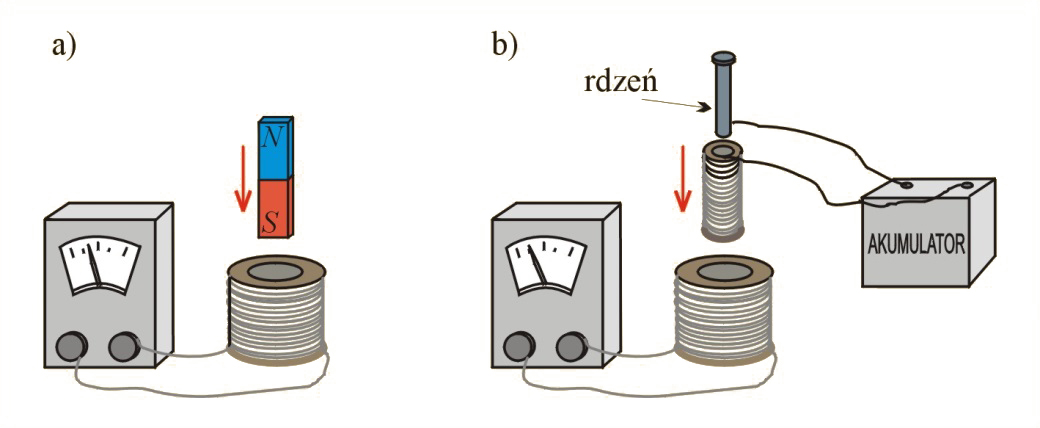 Ilustracja 4.8. a) podczas wkładania magnesu do zwojnicy indukuje się w niej prąd, b) podobny efekt zauważamy podczas wkładania elektromagnesu; rdzeń powoduje zwiększenie prądu indukcyjnego
Ilustracja 4.8. a) podczas wkładania magnesu do zwojnicy indukuje się w niej prąd, b) podobny efekt zauważamy podczas wkładania elektromagnesu; rdzeń powoduje zwiększenie prądu indukcyjnego - Powtarzamy doświadczenia, ale teraz poruszamy dużą cewkę (nasuwając ją lub zdejmując z cewki małej czy magnesu), a magnes lub mała cewka znajdują się w spoczynku. Stwierdzamy, że wychylenia amperomierza są podobne do tych, jakie wystąpiły poprzednio. Zatem powstanie prądu indukcyjnego nie zależy od tego, czy cewka z podłączonym amperomierzem jest w spoczynku, a porusza się źródło pola magnetycznego, czy na odwrót. Ważny jest względny ruch cewki i źródła pola.
Powyższe doświadczenie, podobnie jak opisane na początku rozdziału, potwierdza wniosek, że prąd indukcyjny, więc i siła elektromotoryczna indukcji, pojawiają się w obwodzie, gdy zmienia się w czasie strumień pola magnetycznego przepływający przez obwód.
Obecnie sformułujemy prawo indukcji Faradaya w postaci ilościowej. Posłużymy się omówionym w poprzednim rozdziale przykładem prostego pręta poruszającego się w polu magnetycznym (il. 4.2). Wyprowadziliśmy wzór (4.5) na siłę elektromotoryczną indukcji powstającą w pręcie . Przekształcimy go tak, aby mógł być przydatny w przypadku ogólnym. W tym celu prędkość pręta wyrazimy jako stosunek jego przemieszczenia do czasu : , otrzymamy więc:
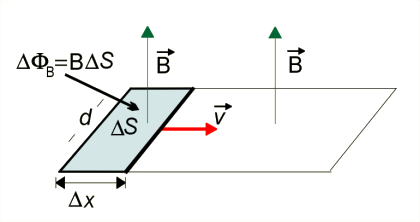
Wyrażenie w liczniku oznacza zmianę strumienia wektora indukcji magnetycznej , gdyż oznacza pole powierzchni zatoczone przez pręt w czasie , a wektor jest prostopadły do tej powierzchni (il. 4.9). Zatem . Otrzymaliśmy wzór, który po opatrzeniu go znakiem minus wyraża prawo indukcji Faradaya:
Wzór (4.7) jest słuszny w ogólnym przypadku i wyraża prawo Faradaya, które słowami można ująć następująco:
Przykład 1
Metalowy pręt o długości wiruje ze stałą częstością w jednorodnym polu magnetycznym o indukcji (il. 4.10). Jak duża SEM indukcji pojawi się w pręcie?
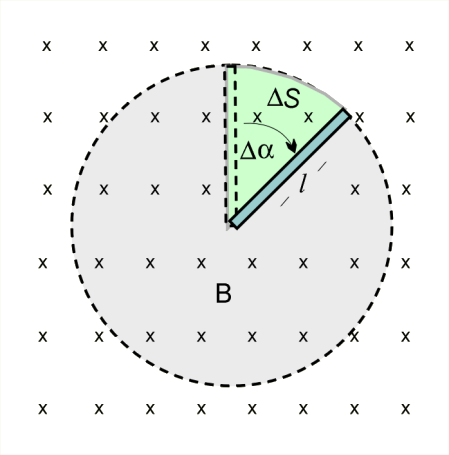
Rozwiązanie: Zgodnie ze wzorem (4.7), SEM zaindukowana w pręcie wynosi:
Pręt w czasie zatacza obszar pola magnetycznego o powierzchni . Pole to jest wycinkiem koła o kącie , więc:
Przyrost strumienia pola , więc:
Skoro , to:
Zatem wartość bezwzględna siły elektromotorycznej indukowanej w pręcie wynosi:
Pytania i problemy
- Czy do tego, aby w obwodzie, przez który przechodzi zmienny strumień pola magnetycznego, płynął prąd, potrzebne jest zewnętrzne źródło prądu?
- W ramach doświadczenia pokazowego 1 przeprowadzono następującą próbę: mniejszą cewkę, bez rdzenia, wstawiono do większej, po czym do mniejszej wstawiono i wyjęto rdzeń ferromagnetyczny. Rozstrzygnij (i odpowiednio uzasadnij), czy uzyskano w ten sposób wychylenie galwanometru.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
