Każdy element (cząstka) ośrodka, w którym rozchodzi się fala, ma energię ruchu drgającego. Fala, przechodząc przez ośrodek, pobudza coraz to nowe cząstki do drgań. W ten sposób fala przenosi energię. Miarą energii fali przenoszonej przez jednostkową powierzchnię w jednostce czasu jest natężenie fali.

Wyobraźmy sobie mały element ośrodka o objętości $V$ i masie $m$. Zgodnie ze wzorem (5.28), średnia energia jego ruchu drgającego wynosi:

Po podzieleniu jej przez objętość $V$, otrzymamy wyrażenie na średnią gęstość energii fali:

gdzie $\rho$ jest gęstością ośrodka. Widzimy, że średnia gęstość energii fali o określonej częstości $\omega$ wynosi:

Jest ona proporcjonalna do kwadratu amplitudy fali.

Fala rozchodzi się w ośrodku, więc przenosi energię między jego elementami. Dla scharakteryzowania wielkości przenoszonej energii w jednostce czasu posługujemy się pojęciem natężenia fali.

Natężeniem fali nazywamy średnią wielkość energii przenoszonej przez jednostkowy wycinek powierzchni falowej w jednostce czasu:

Jest to średnia moc przechodząca przez jednostkowy wycinek powierzchni falowej. Jednostką natężenia fali jest $1\text{W}/{\text{m}}^2$.

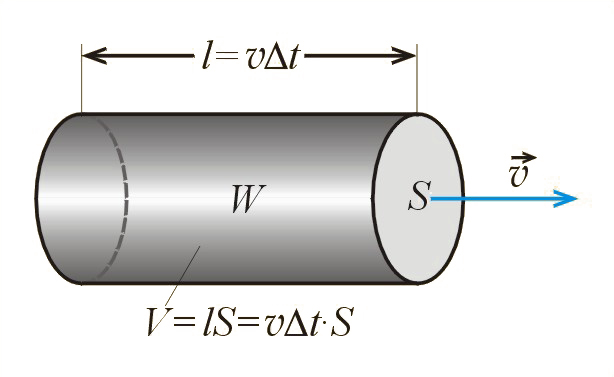
W czasie $\Delta t>T$ przez powierzchnię $S$ przejdzie tyle energii fali, ile jest jej zawarte w objętości $V=lS=v\Delta tS$ (il. 5.23), gdzie $v$ – prędkość fali. Energia $\overline{E}=\overline{w}V=\overline{w}v\Delta tS$. Po podstawieniu tego wyrażenia do (5.48) i skróceniu otrzymamy:

Korzystając ze wzoru (5.47), otrzymamy:

Widzimy, że nie tylko średnia energia, ale również i natężenie fali o określonej częstości jest proporcjonalne do kwadratu jej amplitudy.

Przykład 8

Wewnątrz cylindrycznej rury o średnicy $2R=5\text{cm}$ w powietrzu biegnie fala sinusoidalna. Natężenie fali wynosi $I={10}^{-6}\text{W}/{\text{m}}^2$. Wyznacz energię $W$ przenoszoną przez falę w czasie 1 minuty.

Rozwiązanie: Z wzoru (5.48) mamy:

$$W=IS\Delta t=I\pi R^2\cdot \Delta t={10}^{-6}\cdot \mathrm{3,14}\cdot \mathrm{0,02}{5}^2\cdot 60\text{J}\approx \mathrm{1,2}\cdot {10}^{-7}\text{J}$$

Przykład 9

Chcemy, aby natężenie dźwięków dochodzących do naszych uszu wynosiło $I={10}^{-5}\text{W}/{\text{m}}^2$ (jest to natężenie wystarczająco głośnej muzyki). Przyjmując, że głośnik znajduje się w odległości $r=100\text{m}$, i zakładając, że wysyła fale dźwiękowe jednakowo we wszystkich kierunkach, oblicz, jaka powinna być moc tzw. akustyczna głośnika. Przyjmij, że nie ma pochłaniania energii fali przez powietrze.

Rozwiązanie: Wyobraźmy sobie, że głośnik jest otoczony sferą o promieniu $r$ i powierzchni $4\pi r^2$. Wówczas cała moc $P$ emitowana przez głośnik przejdzie przez tę powierzchnię. Korzystając ze wzoru (5.48) i uwzględniając, że $P=\frac{E}{\Delta t}$, otrzymamy natężenie fali w odległości $r$ od źródła równe $I=\frac{P}{4\pi r^2}$. Stąd:

$$P=4\pi r^{2}I=4\cdot \mathrm{3,14}\cdot {10}^4\cdot {10}^{-5}\text{W}=\mathrm{1,26}\text{W}$$

Zauważmy tutaj, że moc akustyczna głośnika jest znacznie mniejsza od mocy elektrycznej dostarczanej do głośnika, np. ze wzmacniacza. Wynika to z faktu, że typowa sprawność głośnika, czyli stosunek mocy akustycznej do mocy elektrycznej, nie przekracza 5%.

Dla porównania podajmy też, że moc akustyczna ludzkiego narządu mowy (podczas „normalnego” mówienia) jest rzędu $1\text{μ}\text{W}$, a podczas bardzo głośnego śpiewu czy krzyku osiąga $1\text{m}\text{W}$. Z kolei maksymalna moc akustyczna głośników koncertowych mierzona jest w setkach watów.

Pytania i problemy

1. Podaj wzór na średnią energię fali i średnią gęstość fali.
2. Przedstaw związek między natężeniem fali i jej amplitudą.