Celem tego doświadczenia jest zbadanie zależności oporu przewodnika od temperatury i wykazanie, że jest ona liniowa. Zgodnie ze wzorami (2.12) i (2.10) opór przewodnika powinien zależeć od temperatury w następujący sposób:

Mamy wykazać doświadczalnie, że wzór ten zgadza się z rzeczywistą zależnością $R$ od $t$.

Możemy zastosować spiralny przewodnik przygotowany do doświadczenia „Ohm” oraz układ pomiarowy dodatkowo zaopatrzony w wyłącznik (wyłącznik stosujemy po to, by nie wyczerpywać nadmiernie źródła SEM; obwód zamykamy tylko na czas pomiaru). Będziemy badać zależność oporu od temperatury, więc musimy przygotować odpowiednie przyrządy – termometr, pojemnik wykonany z materiału nieprzewodzącego prądu, np. duży kubek porcelanowy lub szklany, grzałkę o małej mocy (najwyżej kilka watów), np. akwariową, oraz olej nieprzewodzący prądu.

W kubku umieszczamy spiralny przewodnik, zalewamy go olejem, a następnie do kubka wkładamy grzałkę i termometr. Dbamy o to, by grzałka była zanurzona możliwie głęboko w cieczy; termometr z kolei umieszczamy tak, by mierzył on temperaturę oleju możliwie blisko spirali. Montujemy układ elektryczny do pomiaru oporu, jak na il. 2.9. Pierwszy pomiar napięcia i natężenia prądu wykonujemy w temperaturze otoczenia. Następnie włączamy grzałkę i czekamy, aż temperatura wzrośnie do $25°\text{C}$, włączamy wyłącznik tylko na czas pomiaru i mierzymy ponownie $U$ oraz $I$. Kolejne pomiary wykonujemy w trakcie wzrastania temperatury co $5°\text{C}$, aż do $90°\text{C}$. Uwaga! Wprawdzie temperatura wrzenia typowych olejów jest wyższa od $100°\text{C}$, jednak jeśli w trakcie doświadczenia zaobserwujemy oznaki wrzenia oleju, bezwzględnie przerywamy dalsze jego podgrzewanie – wrzący olej może się rozchlapać i spowodować poparzenia.

Wyniki pomiarów zapisujemy w tabelce przygotowanej według wzoru pokazanego na il. 2.10. Następnie dla każdej temperatury obliczamy opór. Wyniki również wpisujemy do tej samej tabelki.

Korzystając z danych w tabelce, wyniki pomiarów nanosimy na wykres zależności $R$ od $t$ w postaci punktów. Skalę osi rzędnych (oporu) dobieramy tak, by najmniejsza wartość na skali odpowiadała oporowi $R_0$ dla najniższej temperatury. Zanim poprowadzimy prostą między tymi punktami, umieścimy na wykresie prostokąty niepewności pomiarowych.

W tym celu przeprowadzamy dyskusję niepewności pomiarowych podobną do dyskusji z doświadczenia „Ohm”. Podobnie jak w tamtym doświadczeniu, oceniamy niepewności pomiarów bezpośrednich: temperatury $\Delta t$, napięcia $\Delta U$ i natężenia $\Delta I$, a następnie dla każdego oporu obliczamy niepewność $\Delta R$. Otrzymane wartości wpisujemy do tabelki pomiarów.

Wyniki nanosimy na wykres i rysujemy prostokąty niepewności pomiarowych. Przykładowy wykres pokazano na il. 2.11. Sprawdzamy, przykładając linijkę, czy punkty pomiarowe układają się wzdłuż prostej. Jeżeli tak jest, prostą prowadzimy tak, by przechodziła możliwie przez wszystkie prostokąty.

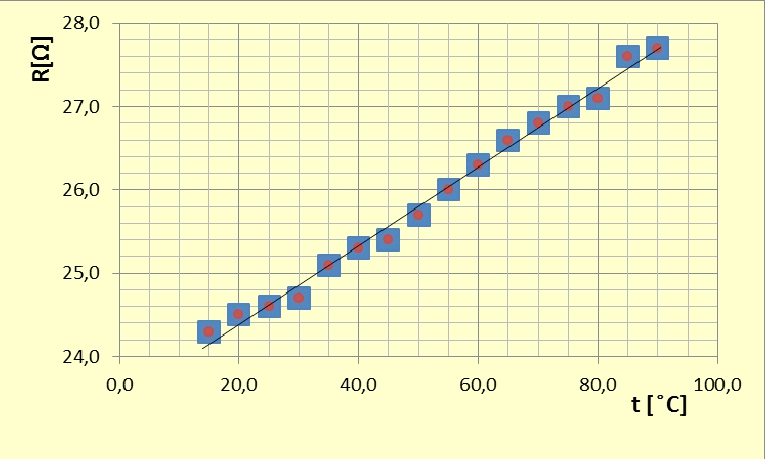
Możliwość przeprowadzenia prostej w pobliżu punktów pomiarowych świadczy o tym, że w naszym doświadczeniu występuje liniowa zależność między oporem przewodnika a jego temperaturą. Zatem upewniamy się w przekonaniu, że wzór (2.15) jest w badanym przedziale zmienności wielkości fizycznych zgodny z rzeczywistością!

Nasze dane pomiarowe pozwalają wyznaczyć współczynnik $\alpha$ dla badanego materiału przewodnika. W tym celu przekształcimy wzór (2.15). Dla temperatur $t_1$ i $t_2$ otrzymamy odpowiednio:

$R_1=R_0\left(1+\alpha t_1\right)$ oraz $R_2=R_0\left(1+\alpha t_2\right)$

Po odjęciu tych równości stronami mamy:

Stąd

Obieramy na prostej na wykresie dwa punkty możliwie najbardziej odległe od siebie i odczytujemy odpowiednie wartości oporu i temperatury, które podstawiamy do wzoru (2.16). Obliczamy wartość $\alpha$. Będzie to nasz wynik końcowy pomiaru.

Sprawdzamy, czy otrzymana przez nas wartość $\alpha$ równa się w przybliżeniu $\frac{1}{273}\frac{1}{°\text{C}}$ (patrz wzór (2.12)). Zapisujemy odpowiedni wniosek.

Jeśli zaś wiemy, z jakiego materiału wykonana jest użyta w doświadczeniu spirala, możemy uzyskaną wartość $\alpha$ porównać z wartością umieszczoną w tablicach wielkości fizycznych.

Powracamy do dyskusji niepewności pomiarowych i obliczamy niepewność pomiaru $\Delta \alpha$. Możemy ją uznać za wielkość złożoną, wyrażoną w postaci ilorazowej, traktując zarówno licznik, jak i mianownik wzoru (2.16) jako pojedyncze wielkości zmierzone z niepewnościami:

$\Delta \left(R_2-R_1\right)=\Delta R_2+\Delta R_1$ oraz $\Delta \left(t_2-t_1\right)=\Delta t_2+\Delta t_1$

(zastosowaliśmy tutaj regułę: niepewność pomiaru różnicy dwóch wielkości jest równa sumie niepewności – patrz tom I, rozdz. 1.D1 Ocena dokładności wyników pomiarów (Dodatek)). Otrzymamy więc wzór:

z którego obliczymy niepewność pomiarową $\Delta \alpha$. Widzimy w tym wzorze zaletę wzięcia do obliczeń wartości $t_1$, $t_2$ oraz $R_1$, $R_2$ możliwie odległych – dzięki temu mianowniki w obu składnikach wzoru (2.17) są duże, a uzyskana niepewność $\Delta \alpha$ mała.