5.8. Równanie fali harmonicznej
Napiszemy teraz równanie, które będzie dawało informacje o wychyleniu dowolnej cząstki w fali harmonicznej w każdej chwili. Znajomość tego równania pozwoli nam rozwiązać wiele problemów związanych z ruchem falowym.
Rozważania nasze przeprowadzimy dla fali poprzecznej, ale wyprowadzone równanie będzie również słuszne dla fali podłużnej.
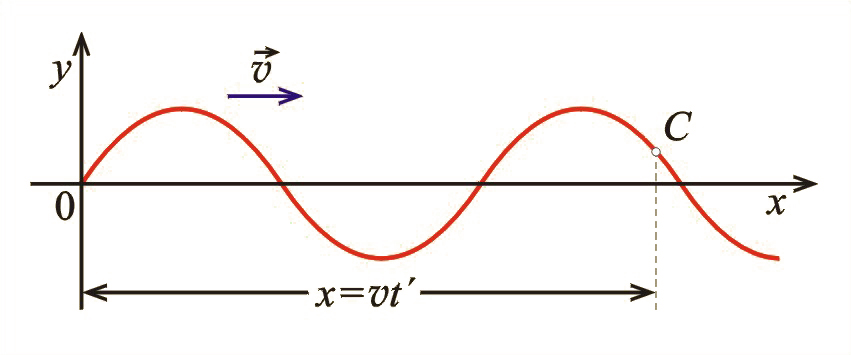
Niech fala rozchodzi się wzdłuż osi , a wychylenia cząstek odbywają się w kierunku równoległym do osi (il. 5.22). Widzieliśmy już na il. 5.19, że każda cząstka, do której dotarła fala, wykonuje takie same drgania harmoniczne, ale opóźnione o czas potrzebny na dotarcie fali do niej. Jeżeli więc wychylenie cząstki drgającej w początku układu współrzędnych jest dane równaniem , to dla cząstki odległej o od cząstki drgania będą się odbywać według takiego samego równania, ale będą opóźnione o czas dotarcia fali do tego miejsca:
Ponieważ ,
Wiemy, że:
oraz że , więc czynnik można przekształcić w następujący sposób:
Po podstawieniu powyższego wzoru oraz (5.40) do równania (5.39) otrzymamy:
Punkt wybraliśmy dowolnie, więc równanie (5.41) jest słuszne dla każdego punktu fali o współrzędnej . Zatem równanie to możemy traktować jako równanie fali harmonicznej, gdzie jest wychyleniem cząstki w punkcie o współrzędnej w chwili . Równanie to będzie słuszne również dla fali podłużnej (wtedy będzie oznaczać wychylenie cząstki równoległe do ).
Wygodnie jest wprowadzić grecką literę oznaczającą wychylenie: , z kolei amplitudę oznaczyć przez . Przy takim oznaczeniu równanie fali:
może opisywać dowolną falę harmoniczną, np. akustyczną – wtedy oznacza ciśnienie drgającego powietrza, falę elektromagnetyczną – wtedy oznacza wektor lub drgającego pola elektromagnetycznego.
Warto zauważyć, że równanie to wykazuje ciekawą symetrię. Jak widać, jest funkcją dwóch zmiennych – czasu i współrzędnej przestrzennej : . Widzimy, że czas i przestrzeń w tej funkcji występują na jednakowych prawach – współrzędna czasowa jest mnożona przez czynnik , określający periodyczność fali w czasie, natomiast współrzędna przestrzenna jest mnożona przez czynnik , określający periodyczność fali w przestrzeni. Czynnik ten nosi nazwę liczby falowej i zwykle oznacza się go literą :
Stwierdzamy, że liczba falowa mówi nam, ile długości fali mieści się na odcinku równym metrów. Podobnie i częstość kołowa mówi nam, ile okresów mieści się w odcinku czasu równym sekund.
Jeżeli zastosujemy te oznaczenia, jednowymiarowe równanie fali harmonicznej przybierze postać:
Przykład 7
Wyznacz prędkość fali, znając jej równanie:
Rozwiązanie: Porównanie ze wzorem (5.44) prowadzi do wniosku, że oraz . Stąd . Gdy zarówno , jak i są dodatnie, fala rozchodzi się w kierunku ujemnych wartości .
Pytania i problemy
- Napisz równanie fali harmonicznej w jednym wymiarze. Objaśnij znaczenie symboli.
- Wyprowadź równanie fali harmonicznej, korzystając z równania drgań harmonicznych.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
