8.14. Przyrządy optyczne
Lupa
W celu określenia zdolności powiększającej lupy potrzebne nam będzie pojęcie odległości dobrego widzenia. Przypomnijmy sobie, co to jest. Aby lepiej widzieć małe przedmioty, zbliżamy je do oka. Zwiększa się wtedy kąt, pod jakim widzimy przedmiot, a jego obraz padający na siatkówkę oka staje się większy. Pamiętamy, że soczewka naszego oka ma zdolność akomodacji, tzn. zmienia swoją grubość i krzywiznę powierzchni wraz ze zmianami odległości przedmiotu od oka. Soczewka oczna zmienia swoją ogniskową, dostosowując ją za każdym razem tak, by obraz na siatkówce był ostry (odległość od soczewki ocznej do siatkówki jest stała). Jednakże akomodacja oka „w bliższy” jest dla oka męcząca; jest ona również ograniczona. Przy zbliżaniu przedmiotu do oka natrafiamy w końcu na taką odległość, po której przekroczeniu przedmiot staje się nieostry, gdyż jego ostry obraz nie może powstać na siatkówce. Zatem odległość dobrego widzenia jest to taka odległość przedmiotu od oka, przy której widzimy go jako ostry, najmniej obciążając przy tym mięśnie oka. Dla przeciętnego oka jest to około 25 cm.
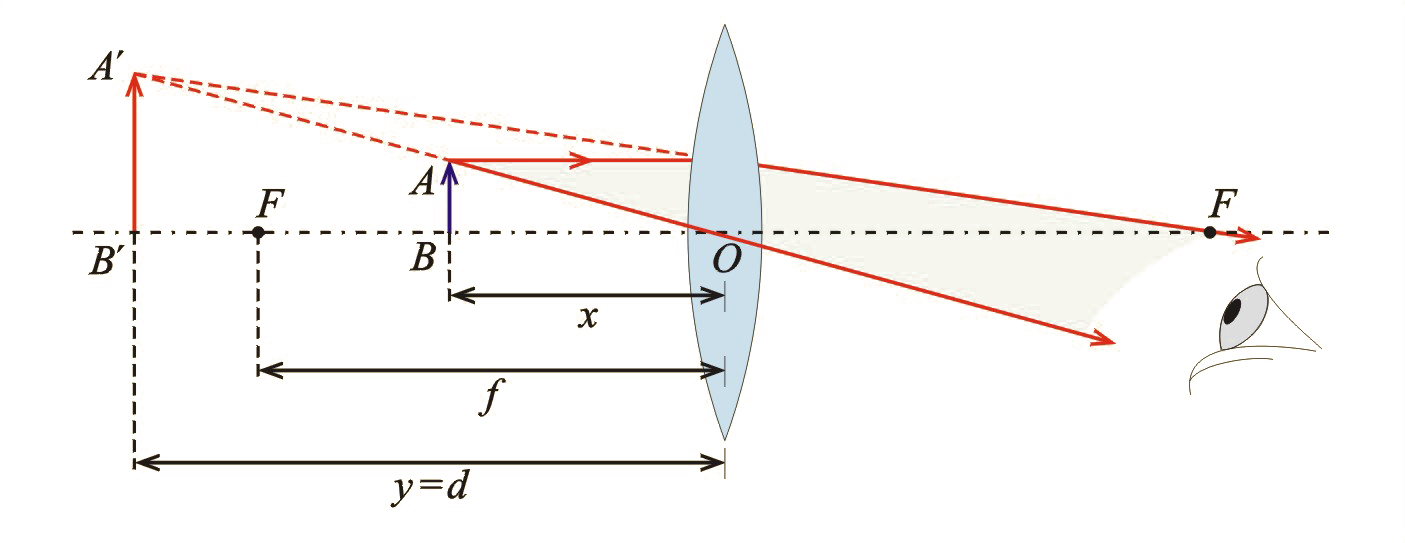
Teraz możemy przejść do omówienia powiększenia lupy. Wiemy, że lupa to pojedyncza soczewka skupiająca, umożliwiająca oglądanie powiększonych obrazów. Bieg promieni w lupie jest pokazany na il. 8.61. Zaznaczono tam ogniskową, odległość przedmiotu od soczewki i odległość y obrazu od soczewki. Standardowo powiększenie lupy podaje się dla sytuacji, w której lupa jest trzymana blisko oka (jak soczewka okularów), a przedmiot jest ustawiany w takiej odległości od lupy, by obraz w niej powstał w odległości dobrego widzenia . Warto zwrócić uwagę, że ta standardowa sytuacja nie zapewnia uzyskania największego powiększenia; największe powiększenie uzyskamy, gdy w przybliżeniu będzie równe najmniejszej odległości, przy której oko może jeszcze akomodować.
Aby wyprowadzić wzór na powiększenie lupy, przeprowadzimy rozumowanie podobne do omówionego w rozdziale 8.11. Soczewka, gdzie powiększenie zdefiniowaliśmy jako stosunek wielkości obrazu do wielkości przedmiotu. Z podobieństwa trójkątów i (il. 8.61) wynika, że:
Wzór soczewkowy (8.52), który dla obrazu pozornego (formalnie jest ujemne) ma postać:
przekształcimy w następujący sposób:
stąd
Ale , więc:
Jest to wzór na powiększenie lupy. Wynika z niego na przykład, że jeżeli lupa ma ogniskową 2,5 cm, a , wówczas powiększenie wynosi 11.
Wydawałoby się, że stosując dowolnie krótkie ogniskowe, można uzyskiwać dowolnie duże powiększenia lupy. Tak jednak nie jest, gdyż wzór (8.57) ma ograniczenia praktyczne – jest tylko wzorem przybliżonym, słusznym dla soczewek cienkich. Soczewka o bardzo małej ogniskowej musi mieć małe promienie krzywizny powierzchni, co powoduje, że nie możemy jej zaliczać do soczewek cienkich. Z kolei im grubsza soczewka, tym trudniej jest uzyskać obraz niezniekształcony. W praktyce lupa nie powiększa więcej niż kilkunastokrotnie.
Mikroskop
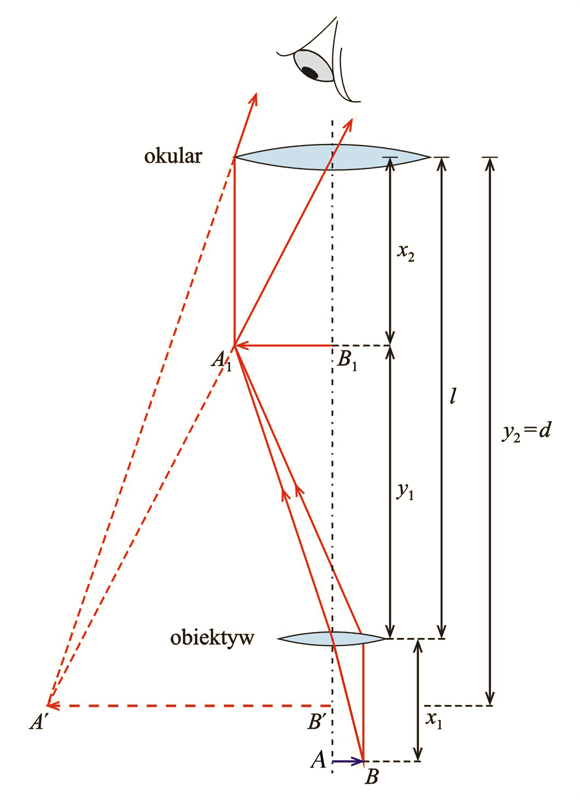
Na il. 8.62 przedstawiono schematycznie bieg promieni w najprostszym mikroskopie. Przedmiot jest umieszczony w odległości nieco większej od ogniskowej obiektywu . Wtedy otrzymujemy duże powiększenie przedmiotu przez soczewkę obiektywu. Obraz jest odwrócony i powstaje w odległości od okularu nieco mniejszej od jego ogniskowej. Możemy więc przyjąć . Odległość obiektywu od okularu jest w przybliżeniu równa długości tubusa mikroskopu. Odległość obrazu od obiektywu jest równa . Wobec tego powiększenie obrazu w soczewce obiektywu wynosi:
Powiększenie obrazu w okularze wynosi (w przybliżeniu):
Całkowite powiększenie obu soczewek mikroskopu wyniesie:
lub
Po podstawieniu tu wyrażeń (8.58) i (8.59) otrzymamy:
Oceniając niezbyt dokładnie powiększenie mikroskopu, można przyjąć wzór przybliżony:
(w liczniku wzoru (8.60) zaniedbaliśmy ogniskową okularu , gdyż jest ona znacznie mniejsza od długości tubusa , np. , ).
Powiększenie zwykle stosowanych obiektywów wynosi od 8 do 90, zaś okularów od 7 do 15. Zatem całkowite powiększenie mikroskopu zwykle mieści się w granicach od 56 do 1350.
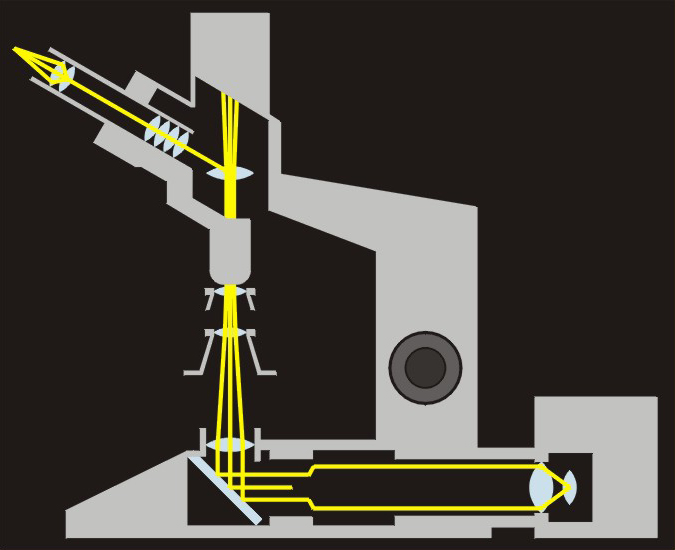
Stosowane w praktyce mikroskopy mają dużo bardziej skomplikowane układy optyczne niż opisany powyżej. Zarówno obiektyw, jak i okular składają się z kilku soczewek (podobnie jak obiektywy aparatów fotograficznych). Są one dobierane pod kątem kształtu i materiału wykonania, by korygować wady obrazu geometryczne (różne odkształcenia) oraz barwne (efekty dyspersji światła). Oprócz obiektywu i okularu w mikroskopie występują układy optyczne zapewniające właściwe oświetlenie oglądanego przedmiotu, kierujące biegiem promieni wewnątrz tubusa czy tworzące promienie przeznaczone do rejestracji na kliszy lub w kamerze. Takie układy przedstawiono schematycznie na il. 8.63.
Współczesna technika komputerowa wprowadziła do mikroskopu ulepszenia, które pozwoliły zwiększyć jakość oglądanych obrazów oraz uzyskiwać powiększenie dochodzące do 7000, tj. ponad pięciokrotnie większe niż w tradycyjnym mikroskopie. Uzyskuje się to przez stosowanie kamer wideo o bardzo wysokiej rozdzielczości z cyfrowym przetwornikiem obrazu i innymi urządzeniami komputerowej obróbki obrazu, pozwalającymi na usuwanie zniekształceń obrazu powstałych w układzie optycznym mikroskopu.
Luneta
Istnieje wiele konstrukcji lunet. My podamy tu zasadę pracy jednej z nich – tzw. lunety Galileusza. Na il. 8.64 przedstawiono bieg promieni w lunecie. Obraz rzeczywisty odległego przedmiotu jest utworzony przez soczewkę skupiającą obiektywu w odległości od niego. Odległość ta jest w przybliżeniu równa ogniskowej obiektywu, tzn. (dzieje się tak, ponieważ przedmiot znajduje się w bardzo dużej odległości od obiektywu, a wówczas na obiektyw padają promienie prawie równoległe). Ten obraz jest oglądany przez drugą soczewkę, tzw. okularu. Okular daje obraz urojony w odległości od niego. Odległość możemy traktować jak odległość dobrego widzenia. Aby w okularze uzyskać duże powiększenie, należy go ustawić w odległości od obrazu równej w przybliżeniu ogniskowej okularu .
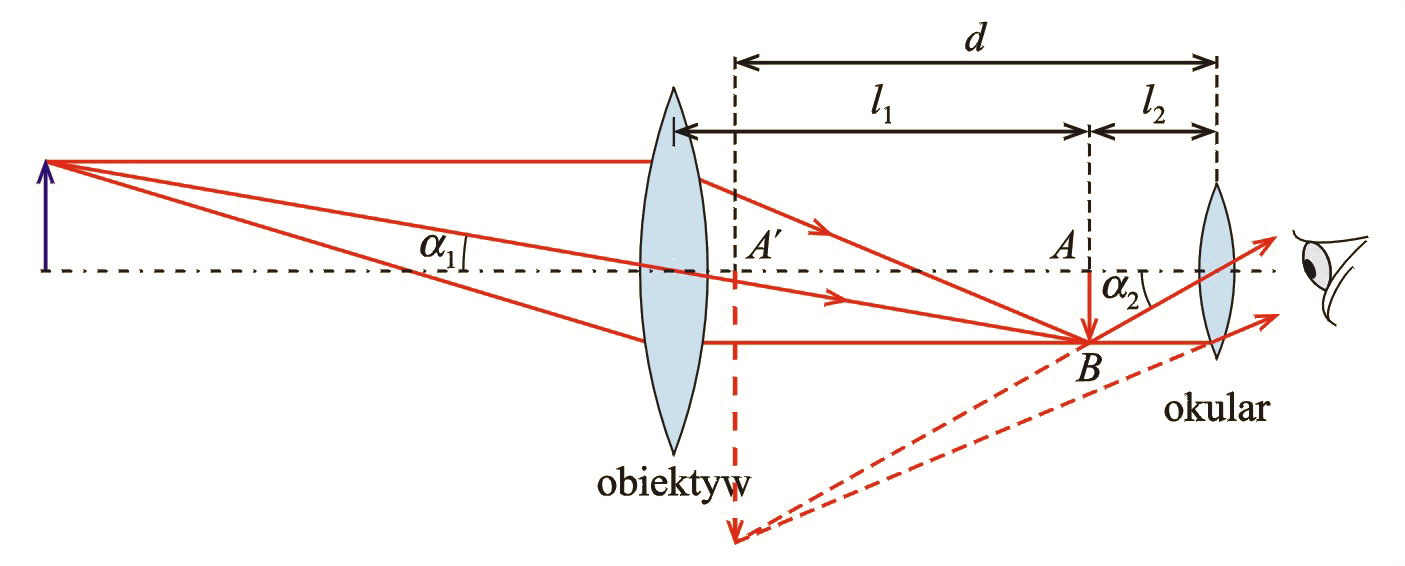
W jaki sposób można określić powiększenie lunety? Otóż gdybyśmy na odległy przedmiot patrzyli okiem nieuzbrojonym, to widzielibyśmy go pod małym kątem . Dlatego przedmiot wydawałby się nam mały – jego obraz na siatkówce oka byłby mały. Patrząc przez okular lunety, widzimy go pod większym kątem (il. 8.64). Przedmiot oglądany przez lunetę wydaje się nam większy. Zatem stosunek drugiego kąta do kąta możemy uznać za powiększenie lunety i wówczas:
Wartości małych kątów możemy przybliżyć ich tangensami . Otrzymamy wtedy:
,
i ostatecznieOtrzymaliśmy wzór na powiększenie lunety:
Widzimy, że aby uzyskać duże powiększenie lunety, należy stosować długie ogniskowe obiektywu, a krótkie ogniskowe okularu.
Niezależnie od tego, że obraz odległego przedmiotu, oglądanego gołym okiem, utworzony na siatkówce oka jest mały, to jeszcze dochodzi drugi czynnik słabego widzenia – bardzo mały jest strumień energii świetlnej płynący do oka. Luneta, oprócz powiększenia obrazu, pełni jeszcze jedną funkcję. Zbiera energię świetlną pochodzącą od oglądanego przedmiotu z większej powierzchni – obiektywu lunety. Przez to strumień świetlny padający do oka jest zwielokrotniony, gdyż strumień ten jest proporcjonalny do powierzchni, na którą pada. Efekt jest taki, jak gdyby źrenica naszego oka zwiększyła się do wielkości obiektywu lunety. Dlatego obiektywy lunet astronomicznych mają duże średnice. Łatwo można obliczyć, że luneta astronomiczna o średnicy obiektywu np. 0,5 m zwiększa strumień energii świetlnej wpadającej do oka około 28 000 razy (przyjęliśmy, że źrenica oka ma średnicę równą około 3 mm).
Pytania i problemy
- Wyjaśnij, co to jest odległość dobrego widzenia. Przedstaw na rysunku mechanizm powstawania obrazu w lupie.
- Wyprowadź równanie opisujące zależność powiększenia lupy od wartości jej ogniskowej. Przedstaw interpretację tej zależności.
- Przedstaw na rysunku mechanizm powstawania obrazu w mikroskopie.
- Wyprowadź równanie opisujące zależność powiększenia mikroskopu od wartości ogniskowej jego obiektywu i okularu. Przedstaw interpretację tej zależności.
- Przedstaw na rysunku mechanizm powstawania obrazu w lunecie.
- Podaj definicję powiększenia lunety i wyprowadź równanie opisujące zależność powiększenia lunety od wartości ogniskowej jej obiektywu i okularu. Przedstaw interpretację tej zależności.
- Znany jest efekt „pomniejszania” obrazu przez lunetę (lornetkę), gdy użyjemy jej „odwrotnie” – spojrzymy w obiektyw zamiast w okular. Omów ten efekt, odwołując się do wzoru (8.63). Wykonaj odpowiedni rysunek.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
