8.2. Doświadczenie „Snellius”
Celem naszego doświadczenia jest upewnienie się o prawdziwości prawa załamania światła – prawa Snelliusa. Przy opracowaniu wyników doświadczenia do powtarzających się obliczeń można wykorzystać komputer. Ćwiczenie można wykorzystać na lekcji informatyki, by odpowiednio skomponować tabelę wyników pomiarów i obliczeń oraz by wykonać wykresy.
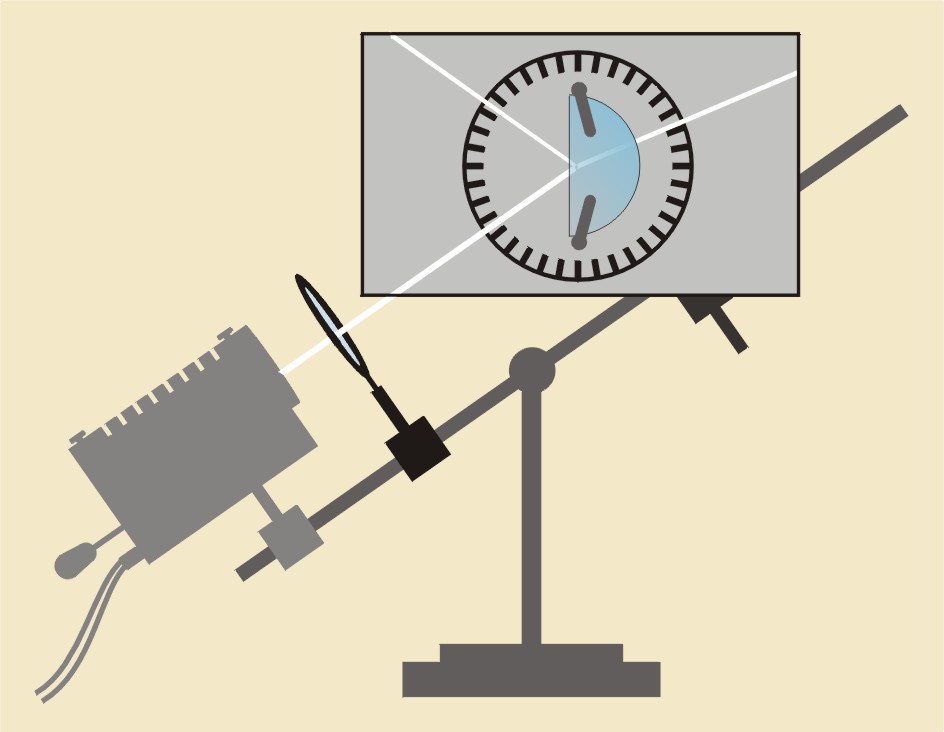
Do wykonania doświadczenia potrzebny będzie prosty przyrząd przedstawiony na il. 8.9. Główną jego częścią jest koło z podziałką stopniową (pełny kątomierz) umieszczone na statywie na osi, aby mogło obracać się wraz z umieszczonym na nim szklanym półkolem. Na statywie znajduje się też wskaźnik laserowy lub latarka z wąską szczeliną umożliwiającą rzucanie wiązki światła na półkole pod dowolnym kątem.
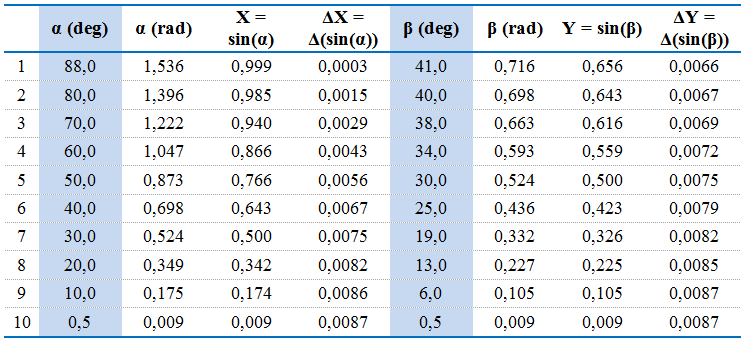
Ustawiamy koło kątomierza wraz z półkolem szklanym tak, aby kąt padania wiązki światła na płaską powierzchnię półkola szklanego wynosił zero. Sprawdzamy, czy kąt załamania (wyjścia wiązki po drugiej stronie półkola) także wynosi zero. W przeciwnym razie odpowiednio korygujemy ustawienie półkola na tle kątomierza. Następnie nastawiamy kąt padania bliski , np. . Staramy się zmierzyć kąt załamania (w razie niemożności dokonania odczytu, zmniejszamy kąt o i ponawiamy próbę). Powtarzamy pomiary kątów, zmieniając stopniowo kąt padania, np. , , ,… , . Wyniki pomiarów wpisujemy do odpowiednio przygotowanej tabelki (il. 8.10). Wykonujemy także wykres zależności (il. 8.11) na podstawie wyróżnionych kolumn.
Wstępna analiza wyników pomiarów
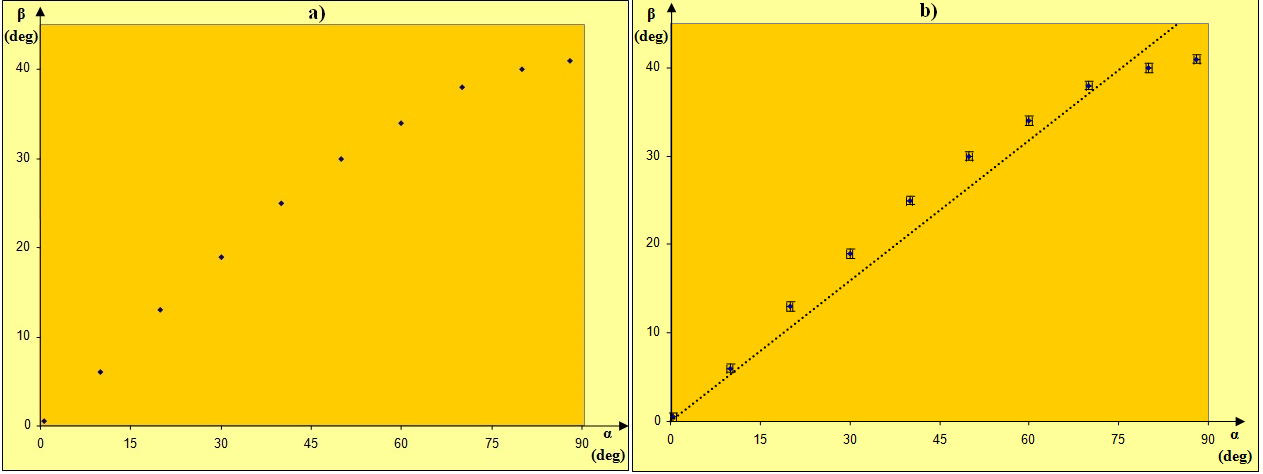
Stwierdzamy, że punkty pomiarowe układają się w określonym porządku. Żaden z punktów nie odstaje w sposób znaczący od tego porządku, co świadczy o wykonaniu pomiarów bez popełnienia błędu grubego (pomyłki).
Zauważamy, że porządek ułożenia punktów nie jest wyznaczony przez linię prostą – na il. 8.11b poprowadzono prostą optymalną przechodzącą możliwie blisko wszystkich punktów pomiarowych. Prosta ta przechodzi jednak tylko przez niewielką część prostokątów niepewności. Odchylenia punktów od tej prostej mają charakter systematyczny, świadczący o ułożeniu punktów wzdłuż linii krzywej.
Powyższe stwierdzenie prowadzi nas do wniosku, że zależność nie jest liniowa. Jest to zgodne z prawem Snelliusa (8.3), które łączy zależnością liniową sinusy kątów padania i załamania światła. Dalsze postępowanie idzie w kierunku „wyprostowania” uzyskanej zależności, podobnie jak to uczyniliśmy przy okazji doświadczeń „Akceleracja” (rozdz. 1.13. Doświadczenie „Akceleracja”, tom II) i „AkceleracjaBIS” (rozdz. Doświadczenie „Akceleracja BIS”, tom II).
Analiza przekształconych wyników pomiarów
Z prawa załamania światła (8.3) wynika, że:
czyli
co można zapisać jako . Jest to zależność liniowa, w której pomocnicza zmienna , zaś pomocnicza zmienna . Symbolem oznaczyliśmy współczynnik kierunkowy zależności , równy odwrotności współczynnika załamania .
Obliczamy wartości sinusów kątów i (zamieniwszy uprzednio ich miary ze stopni na radiany) i wpisujemy je do odpowiednich kolumn tabelki pomiarów (il. 8.10). Każdej wartości sinusa kąta przypisujemy też niepewność pomiarową. Wynika ona przede wszystkim z niepewności wyznaczania samych kątów i . Ocenimy je, przyjmując za podstawę dokładność skali kątomierza oraz szerokość wiązki światła. W opisanym tu doświadczeniu przyjęto, że .
Mając te wartości, możemy ocenić i . Niepewności te będą różne, gdyż funkcja sinus nie jest liniowa. Dla dowolnego kąta niepewność jego sinusa zapisujemy jako:
Wykonujemy wykres zależności od w ten sposób, że na osi odciętych odkładamy wartości , zaś na osi rzędnych – wartości (il. 8.12a). Punkty pomiarowe otaczamy prostokątami niepewności pomiarowej i prowadzimy prostą optymalną możliwie blisko wszystkich punktów. Uwaga: Wykres należy wykonać w odpowiedniej skali, by uwidocznić niepewności pomiarowe, które są tu małe.
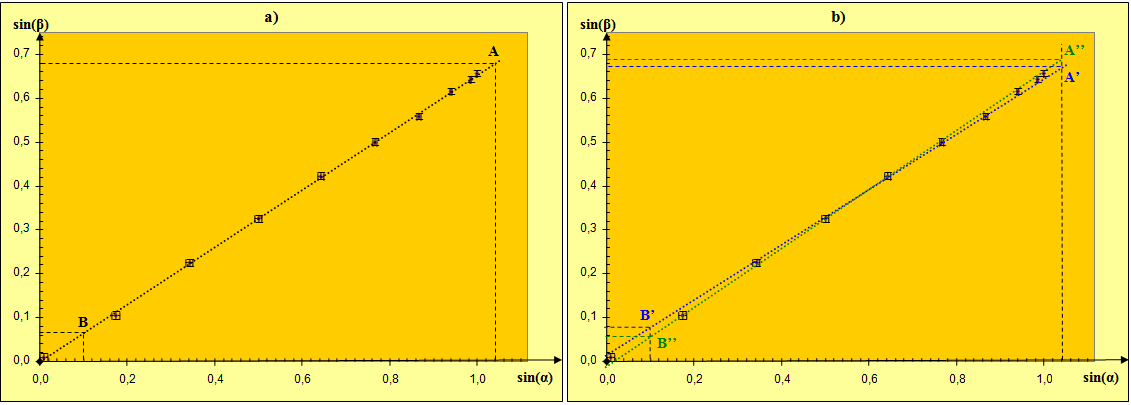
Cieszymy się, jeżeli punkty na wykresie układają się w pobliżu prostej optymalnej, a ta przechodzi przez wszystkie prostokąty niepewności, gdyż świadczy to o tym, że potwierdziliśmy doświadczalnie prawo załamania światła!
Obliczenie współczynnika załamania światła
Wartość współczynnika kierunkowego prostej optymalnej określa nam odwrotność wartości współczynnika załamania ośrodka półkola (szkła) względem powietrza (8.9). Współczynnik kierunkowy prostej zaś jest tożsamy z jej nachyleniem do osi (czyli ). Nachylenie to obliczamy, korzystając z wykresu na il. 8.12a i z pomocniczych punktów i umieszczonych na prostej optymalnej – stosujemy przy tym postępowanie opisane w doświadczeniu „AkceleracjaBIS” (rozdz. 4.9. Doświadczenie „Akceleracja BIS”, tom II).
Odczytana z wykresu wartość współczynnika kierunkowego (w tym doświadczeniu jest to wielkość niemianowana) odpowiada współczynnikowi załamania:
Niepewność pomiarową szacujemy na podstawie wykresu na il. 8.12b, nadal stosując postępowanie opisane w doświadczeniu „AkceleracjaBIS” (rozdz. 4.9. Doświadczenie „Akceleracja BIS”, tom II). Kreślimy dwie skrajne proste przechodzące przez wszystkie prostokąty niepewności. Nachylenie prostej niebieskiej z punktami i pozwoli nam obliczyć maksymalną dopuszczalną wartość :
Podobnie, nachylenie prostej zielonej z punktami i pozwala nam obliczyć minimalną dopuszczalną wartość :
Oszacowana maksymalna niepewność pomiarowa jest połową różnicy pomiędzy a :
Po dokonaniu odpowiednich zaokrągleń, zapisujemy współczynnik załamania szkła, z którego zrobione było półkole jako:
Względna niepewność pomiarowa .
Podsumowanie
Wszystkie postawione cele doświadczenia zostały osiągnięte. Zmierzone kąty padania i załamania światła ułożyły się na wykresie na linii krzywej, czego należało oczekiwać. Z kolei na wykresie punkty ułożyły się na linii prostej, co jest zgodne z przewidywaniami prawa załamania światła (prawa Snelliusa).
W doświadczeniu nie popełniono istotnych błędów (pomyłek), a odstępstwa punktów od optymalnej linii prostej na wykresie miały losowy charakter i mieściły się w granicach niepewności pomiarowej.
Zastosowana graficzna metoda wyznaczenia współczynnika załamania światła w szkle i oszacowania jego niepewności pomiarowej dała wynik:
co oznacza względną niepewność pomiarową 3,3%, bardzo przyzwoitą jak na szkolne warunki.
Wynik ten, uzyskany dla żarowego światła latarki, jest zgodny z wartością wzorcową (tabela na il. 8.6, rozdział 8.1. Prawa odbicia i załamania światła). Wartość ta jest wprawdzie podana dla światła żółtego, ale można przyjąć, że żółte światło odpowiada z grubsza środkowi widma widzialnego.
Pytania i problemy
- Przedstaw powód, dla którego w opisanym doświadczeniu badamy zjawisko załamania przy wejściu światła z powietrza do szkła, zaś nie zajmujemy się załamaniem światła przy przejściu ze szklanego półkola z powrotem do powietrza. Czy to drugie załamanie nie fałszuje wyników pomiarów? Uzasadnij swoją odpowiedź.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
