Ocena niepewności pomiarowych napięcia i natężenia prądu

W przypadku mierników analogowych przyjmuje się, że niepewność pomiaru to połowa wartości najmniejszej działki przyrządu pomiarowego powiększona o wartość wynikającą z tzw. klasy przyrządu pomiarowego. Zilustrujemy to za pomocą przykładu pokazanego na il. 2.28.

W przypadku mierników cyfrowych konieczne jest zapoznanie się z instrukcją załączoną do miernika. Wynika to przede wszystkim z faktu, że mierniki takie mają na ogół wiele zakresów, a klasa miernika może zależeć od używanego zakresu. Inna (niż przy miernikach analogowych) jest też na ogół interpretacja klasy miernika: określa ona względną niepewność odczytu. Podobnie jak w przypadku mierników analogowych, oprócz klasy miernika należy uwzględnić niepewność związaną ze skalą, czyli z ostatnią wyświetlaną cyfrą znaczącą. Zilustrujemy to w sześciu krokach na przykładzie pokazanym na il. 2.29 oraz na podstawie danych w tabeli na il. 2.29.

4. W tabeli na il. 2.29 pokazano, że zakresy miernika dobrane są w tzw. dekady. Dla każdej dekady podana jest rozdzielczość odczytu – jest to odpowiednik najmniejszej podziałki na skali miernika analogowego. W zakresie 20 V wskazania są podane do setnych części wolta.

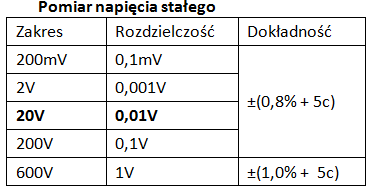
5. Dla każdego zakresu podano „dokładność” (czyli niepewność) odczytu. Dla zakresu 20 V $\text{„}\pm \mathrm{0,8}\%\text{”}$ jest odpowiednikiem klasy miernika i oznacza, że niepewność związana z klasą to 0,8% razy odczyt. Z kolei $\text{„}\pm 5c\text{”}$ oznacza, że niepewność związana z podziałką wynosi pięć jednostek na ostatniej cyfrze określonej rozdzielczością, czyli 0,05 V dla skali 20-woltowej.

6. Tak więc całkowita niepewność pomiarowa napięcia $\Delta U=\mathrm{0,8}\%\cdot U+\mathrm{0,05}\text{V}\approx \mathrm{0,036}\text{V}+\mathrm{0,05}\text{V}=\mathrm{0,086}\text{V}$. Ostatecznie więc mierzone napięcie $U=\mathrm{4,53}\text{V}\pm \mathrm{0,086}\text{V}$.

Warto zwrócić uwagę, że wynik ten jest niemal dwukrotnie bardziej precyzyjny niż wynik uzyskany za pomocą woltomierza analogowego (w obu przypadkach mierzono napięcie na zaciskach tej samej baterii płaskiej). W naszym przykładzie wynika to z różnic klas przyrządów, choć istnieją precyzyjne mierniki analogowe o klasie lepszej niż wiele mierników cyfrowych.

Pomiar oporu elektrycznego

Zgodnie z prawem Ohma $R=\frac{U}{I}$, zatem, aby zmierzyć opór przewodnika $R$, należy znać zarówno natężenie prądu $I$ płynącego w przewodniku, jak i napięcie $U$ na jego końcach. Trzeba więc zbudować obwód elektryczny, w najprostszym przypadku taki, jak na il. 2.31. Woltomierz łączymy równolegle do badanego opornika, a amperomierz – szeregowo.

Woltomierz powinien mieć duży opór wewnętrzny, aby zabierać jak najmniejszy prąd z obwodu i w możliwie małym stopniu zmieniać prąd płynący przez opór $R$. Amperomierz zaś powinien mieć mały opór, aby wprowadzać jak najmniejszą zmianę potencjału w gałęzi obwodu, w której się znajduje. Ponieważ amperomierz w naszym przykładowym obwodzie znajduje się przed punktem $B$, gdzie dołączony jest woltomierz, więc wskazuje całkowite natężenie prądu – zarówno tego, który przepływa przez woltomierz, jak i tego, który nas interesuje, przepływającego przez opornik o oporze $R$. Amperomierz możemy umieścić za punktem $B$ – wtedy jego wskazania nie będą zawierały natężenia prądu płynącego przez woltomierz, ale za to woltomierz będzie wskazywał łączną różnicę potencjałów na oporniku o oporze $R$ i na amperomierzu.

Pomiar siły elektromotorycznej $E$

W obwodzie pokazanym na il. 2.31 woltomierz mierzy napięcie na oporniku o oporze $R$. Jak jednak zmierzyć siłę elektromotoryczną $E$?

Napięcie $U$, które mierzy woltomierz w tym obwodzie, jest jednocześnie napięciem na zaciskach źródła (pomijając małą zmianę potencjału wniesioną przez amperomierz). To napięcie $U=IR$ nie jest równe sile elektromotorycznej $E$, gdyż zgodnie z prawem Ohma dla całego obwodu:

więc:

Jeżeli do obwodu włączy się regulowany opornik, zwany potencjometrem, jak na il. 2.32, to zwiększając wartość oporu $R$ (ruch suwaka potencjometru w górę), można obserwować wzrost napięcia wskazywanego przez woltomierz. Wykres zależności napięcia $U$ od wartości oporu $R$ opisanej za pomocą równania (2.42) przedstawiony jest na il. 2.33a. Widzimy, że im większy opór zewnętrzny $R$, tym bardziej napięcie $U$ zbliża się do wartości siły elektromotorycznej $E$. Jeżeli wyłączymy opornik $R$ za pomocą wyłącznika $K$, to prąd popłynie tylko przez woltomierz, który ma zwykle duży opór. Wtedy jego wskazanie mało już będzie się różnić od wartości $E$. Widzimy na wykresie, że teoretycznie wartość siły elektromotorycznej będzie równa napięciu na zaciskach źródła wtedy, gdy opór będzie nieskończenie duży, a to następuje, gdy źródło jest otwarte (dlatego czasami mówi się, że wartość siły elektromotorycznej jest równa napięciu na zaciskach źródła otwartego). Wtedy natężenie prądu w obwodzie zbliża się do zera, co jest widoczne na wykresie zależności (2.41) – il. 2.33b.

Wykres na il. 2.33b pokazuje jeszcze jeden ciekawy aspekt korzystania ze źródeł prądu. Nawet jeśli jego zaciski połączymy idealnym przewodem, o oporze $R=0$ (czyli doprowadzimy do tzw. zwarcia źródła), to nie uzyskamy przepływu prądu o dowolnie dużym natężeniu. Maksymalne natężenie prądu, jaki możemy czerpać ze źródła, tzw. prąd zwarcia $I_0$, zależy od SEM $E$ źródła oraz oporu wewnętrznego $r$ i wynosi:

Duża wartość prądu zwarcia często jest pożądaną cechą akumulatorów (np. samochodowych), które muszą być w stanie dostarczyć prądu o dużym natężeniu (nawet rzędu 100–200 A), by zapewnić rozruch silnika.

Bezpośredni pomiar SEM

Jeśli w obwodzie (il. 2.32) ustawimy dwie różne wartości oporu potencjometru $R_1$ i $R_2$ i zmierzymy odpowiadające im $\left(I_1;U_1\right)$ oraz $\left(I_2;U_2\right)$, to możemy wyznaczyć SEM $E$ oraz opór wewnętrzny $r$ źródła.

Metoda kompensacyjna

W praktyce istnieje sposób na precyzyjny pomiar wartości SEM bez konieczności stosowania oporników o bardzo dużych oporach. Jest to tzw. metoda kompensacji. Schemat obwodu jest pokazany na il. 2.34. Zaznaczono tam natężenia prądów i wartości SEM. Symbolem $E_x$ oznaczono mierzoną wartość SEM, a $E_0$ oznacza wartość SEM źródła zasilającego układ. Dzięki potencjometrowi $R_0$ można regulować napięcie podawane na drugi potencjometr o końcach $AB$. Natężenie prądu w części $AC$ tego potencjometru wynosi $\left(I_0-I\right)$, co wynika z pierwszego prawa Kirchhoffa w odniesieniu do węzła $C$. Zgodnie z drugim prawem Kirchhoffa dla oczka oznaczonego $ACDE$ mamy:

Z tego równania możemy wyznaczyć wartość $I$:

Widzimy, że – zmieniając opór $R_{AC}$ – możemy tak dobrać jego wartość, aby prąd w oczku $ACDE$ nie płynął. Wtedy $I=0$, co wykaże nam czuły galwanometr $G$. Oznaczmy tę wartość oporu przez $R_x$. Wtedy:

Widzimy, że wartość $E_x$ możemy wyznaczyć, mierząc $I_0$ i $R_x$. Zwykle jednak postępujemy inaczej. Po zmierzeniu $R_x$ w miejsce źródła o nieznanej wartości $E_x$ wstawiamy źródło wzorcowe $E_w$. Ponownie doprowadzamy do wyzerowania wskazań galwanometru, co następuje przy innej wartości oporu $R_{AC}$, którą oznaczymy jako $R_w$. Otrzymamy wtedy (przyjmując, że $I_0$ pozostaje niezmienione, co uzyskujemy, odpowiednio przesuwając suwak potencjometru $R_0$):

Stąd, po uwzględnieniu (2.45), otrzymamy wzór:

pozwalający na precyzyjne wyznaczenie nieznanej wartości $E_x$. Warto zauważyć, że opór wewnętrzny $r$ badanego źródła nie odgrywa tu żadnej roli. Przyrządy do wyznaczania wartości SEM zawierają zwykle w jednej obudowie źródło zasilania $E_0$ i wzorcowe $E_{\mathrm{w}}$, przełączniki pozwalające na zamianę badanego źródła ze źródłem wzorcowym oraz urządzenie zapewniające precyzyjne utrzymanie stałej wartości $I_0$.