Fala harmoniczna to fala sinusoidalna, tzn. taka, w której drgania zachodzą zgodnie z funkcją sinus (lub kosinus). Ze złożenia fal harmonicznych można otrzymać wiele innych fal.

Jeżeli w doświadczeniu pokazowym zamiast uderzać dłonią w sznur będziemy potrząsać jego końcem, wprowadzając sznur w ruch drgający harmoniczny, to w sznurze wytworzy się fala w postaci sinusoidy. Przeanalizujmy teraz to zjawisko dokładniej, co pozwoli nam odpowiedzieć na pytanie, dlaczego tak się dzieje. Wyróżnijmy na rysunku sznura cząstki i ponumerujmy je (il. 5.19a). Cząstkę $1$ pobudzamy do drgań harmonicznych o okresie $T$. Poszczególne fazy ruchu są przedstawione na il. 5.19b-e.

Na il. 5.19b pokazano moment, gdy cząstka $1$ osiągnęła swoje największe wychylenie – po czasie równym $\frac{T}{4}$. Cząstka $2$ pociągnięta przez cząstkę $1$ została również pobudzona do drgań. Jednakże wymagało to pewnego czasu, co powoduje, że cząstka $2$ po jednej czwartej okresu nie osiągnęła jeszcze swojego najwyższego wychylenia i ciągle porusza się w górę, cząstka $3$ jeszcze bardziej się opóźnia, a cząstka $4$ i następne jeszcze nie rozpoczęły ruchu drgającego.

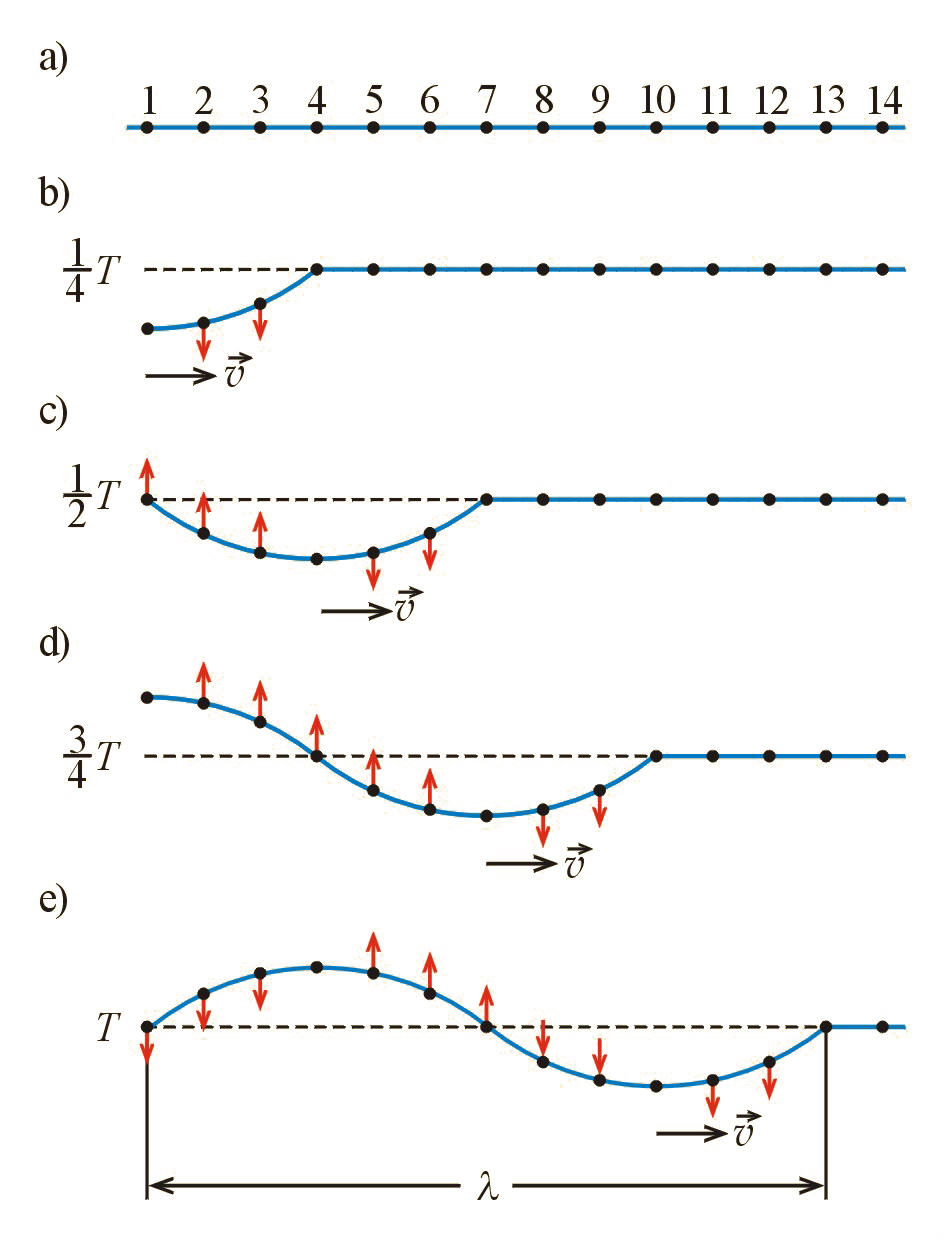
Na il. 5.19c przedstawiona jest sytuacja po czasie równym połowie okresu. Cząstka $1$ wróciła do miejsca początkowego, ale ma prędkość zwróconą w dół, co zaznaczono strzałką. Cząstka $2$ po osiągnięciu swojego największego wychylenia zmierza w dół, podobnie cząstka $3$. Teraz cząstka $4$ ma największe wychylenie, zaś cząstki $5$ i $6$ zostały pobudzone do ruchu w górę (podobnie jak to było z cząstkami $2$ i $3$ po czasie $\frac{T}{4}$). W efekcie oddziaływania sprężystego cząstek po połowie okresu ułożą się w kształcie połówki sinusoidy.

Rozumując podobnie, dojdziemy do wniosku, że po czasie równym $\frac{3T}{4}$ cząstki ułożą się jak na il. 5.19d, zaś po czasie $T$ – tak, jak na il. 5.19e. Widzimy, że po pełnym okresie cząstki ułożą się na sinusoidzie i w tym czasie fala dotrze do cząstki $13$.

Odległość, jaką fala przebędzie w czasie jednego pełnego okresu, nazywamy długością fali i oznaczamy $\lambda$. Jasne jest, że prędkość rozchodzenia się fali wynosi:

Występujący tu okres $T$ drgań cząstki w ruchu falowym nosi nazwę okresu fali. Podobnie jak w ruchu drgającym, częstotliwość fali definiuje się jako odwrotność okresu:

Zatem, zgodnie ze wzorem (5.35), prędkość fali można wyrazić za pomocą wzoru:

Prędkość rozchodzenia się fali w danym ośrodku jest stała i zależy tylko od własności tego ośrodka.

Zatem ze wzoru (5.37) wnioskujemy, że iloczyn częstotliwości i długości fali dla danego ośrodka jest stały. To oznacza, że jeżeli w ośrodku wzbudzimy drgania o większej częstotliwości, rozchodząca się fala będzie miała mniejszą długość lub – ściślej – długość fali w danym ośrodku jest odwrotnie proporcjonalna do jej częstotliwości (co symbolicznie zapisujemy: $\lambda =\frac{v}{\nu }$ lub $\lambda \sim \frac{1}{\nu }$). Czyli fale o większej częstotliwości są krótsze.

Wartość maksymalną wychylenia cząstki z położenia równowagi nazywamy amplitudą fali i zwykle oznaczamy przez $A$.

Przyjrzyjmy się jeszcze raz il. 5.19. Mimo iż cząstki drgają w określonych miejscach w górę i w dół w stosunku do położenia równowagi, fala się przemieszcza.

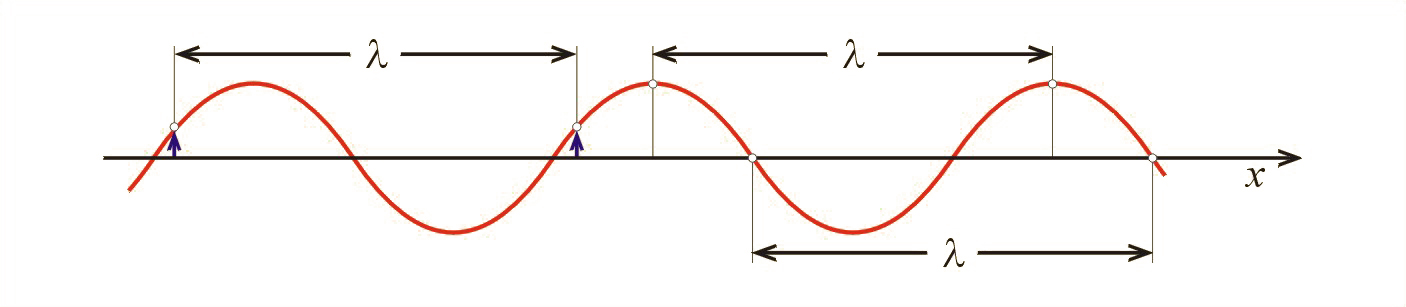
Na rysunku poziomą strzałką zaznaczono ruch „grzbietu” fali, tzn. przemieszczanie się maksymalnego wychylenia (z lewa na prawo). Widzimy, że w tym przypadku ruch fali polega na przemieszczaniu się poszczególnych faz drgających cząstek. Zauważmy, że w fali harmonicznej jest wiele cząstek mających w danej chwili taką samą fazę (il. 5.20), tzn. cząstek, które mają jednakowe wychylenia z położenia równowagi i jednakowy zwrot prędkości chwilowej. Mówimy, że te cząstki mają zgodne fazy. Na przykład na il. 5.19e cząstki $1$ i $13$ mają zgodne fazy. Dwie najbliższe cząstki mające zgodne fazy znajdują się w odległości równej długości fali $\lambda$ (il. 5.20).

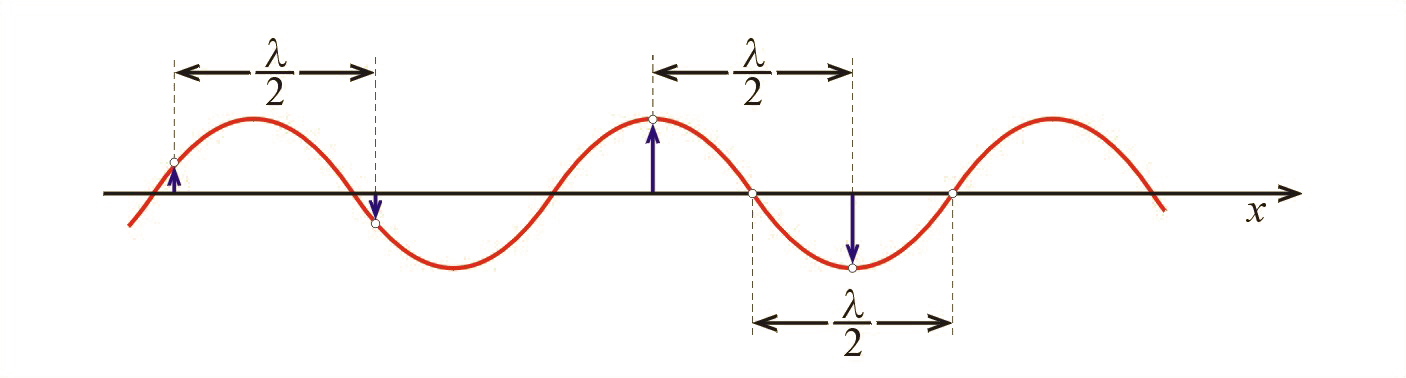
O dwóch cząstkach, które mają wychylenia i prędkości jednakowej wartości, ale przeciwnego zwrotu (il. 5.21), mówimy, że mają fazy przeciwne. Na przykład na il. 5.19e fazy przeciwne mają cząstki $1$ i $7$, $2$ i $8$, $3$ i $9$ itd. Dwie najbliższe cząstki mające fazy przeciwne znajdują się w odległości równej połowie długości fali.

Wszystko, co podano powyżej, odnosi się również do fal podłużnych.

Przykład 6

Wiemy, że prędkość rozchodzenia się fal dźwiękowych w powietrzu wynosi $v=340\text{m}/\text{s}$. Wyznacz długość fali dźwiękowej rozchodzącej się od kamertonu, który wydaje dźwięk o częstotliwości $\nu =440\text{Hz}$.

Rozwiązanie: Korzystając ze wzoru (5.37), mamy $\lambda =\frac{v}{\nu }$, więc:

$$\lambda =\frac{v}{\nu }=\frac{340}{440}\text{m}=\mathrm{0,773}\text{m}=\mathrm{77,3}\text{cm}$$

Długość fali dźwiękowej emitowanej przez ten kamerton wynosi $\lambda =\mathrm{77,3}\text{cm}$.

Pytania i problemy

1. Jaką falę nazywamy falą harmoniczną? Wyjaśnij, co rozumiesz przez: długość fali, okres, częstotliwość oraz prędkość fali. Opisz związki między tymi wielkościami.
2. Gdy fale sejsmiczne przechodzą przez warstwy wnętrza Ziemi o różnej gęstości, to dochodzi do zmiany prędkości rozchodzenia się tych fal. Rozstrzygnij, czy towarzyszy temu zmiana częstotliwości fali, czy długości fali. Uzasadnij swoje rozstrzygnięcie.
3. Czy w jednym określonym ośrodku możemy wzbudzić fale o różnych częstotliwościach? Określ związek między długością fali i jej częstotliwością.
4. Podaj definicje amplitudy fali i fazy fali. Kiedy cząstki ośrodka mają fazy zgodne, a kiedy – przeciwne?