5.6. Podstawowe cechy fal
Zjawiska polegające na rozchodzeniu się fal występują w przyrodzie bardzo często. Obserwujemy je w postaci fal na wodzie. Rozchodzenie się drgań w powietrzu to fale akustyczne, dzięki którym możemy się porozumiewać i słuchać muzyki. Rozchodzenie się w przestrzeni zmiennych pól, elektrycznego i magnetycznego, to fale elektromagnetyczne, do których należą fale radiowe i radarowe służące do telekomunikacji. Do fal elektromagnetycznych należy też światło. Tego rodzaju zjawiska spotykamy także w mikroświecie, gdyż zachowanie się cząstek elementarnych ma również charakter falowy.
Najłatwiejsze do obserwacji są fale mechaniczne. Na ich przykładzie zrozumiemy podstawowe prawa ruchu falowego. Dlatego od nich rozpoczniemy omawianie zjawisk falowych. Wyróżnimy fale poprzeczne i podłużne, dowiemy się, dlaczego fale rozchodzą się w ośrodku ze skończoną prędkością, a nie błyskawicznie. Fale elektromagnetyczne, m.in. radiowe i świetlne, omówimy w dalszych częściach podręcznika.
Wykonamy doświadczenia dotyczące ruchu fali mechanicznej i wyciągniemy z nich wnioski dotyczące fal w ogólności.
Doświadczenie pokazowe 1
Weźmy długi sznur (5, 6 metrów) i umocujmy go jednym końcem do ściany. Drugi koniec trzymajmy w ręku. Uderzając grzbietem dłoni w sznur, przekonamy się, że powstałe wygięcie (odkształcenie) sznura nie pozostaje w spoczynku, ale porusza się wzdłuż sznura, jak na il. 5.16.
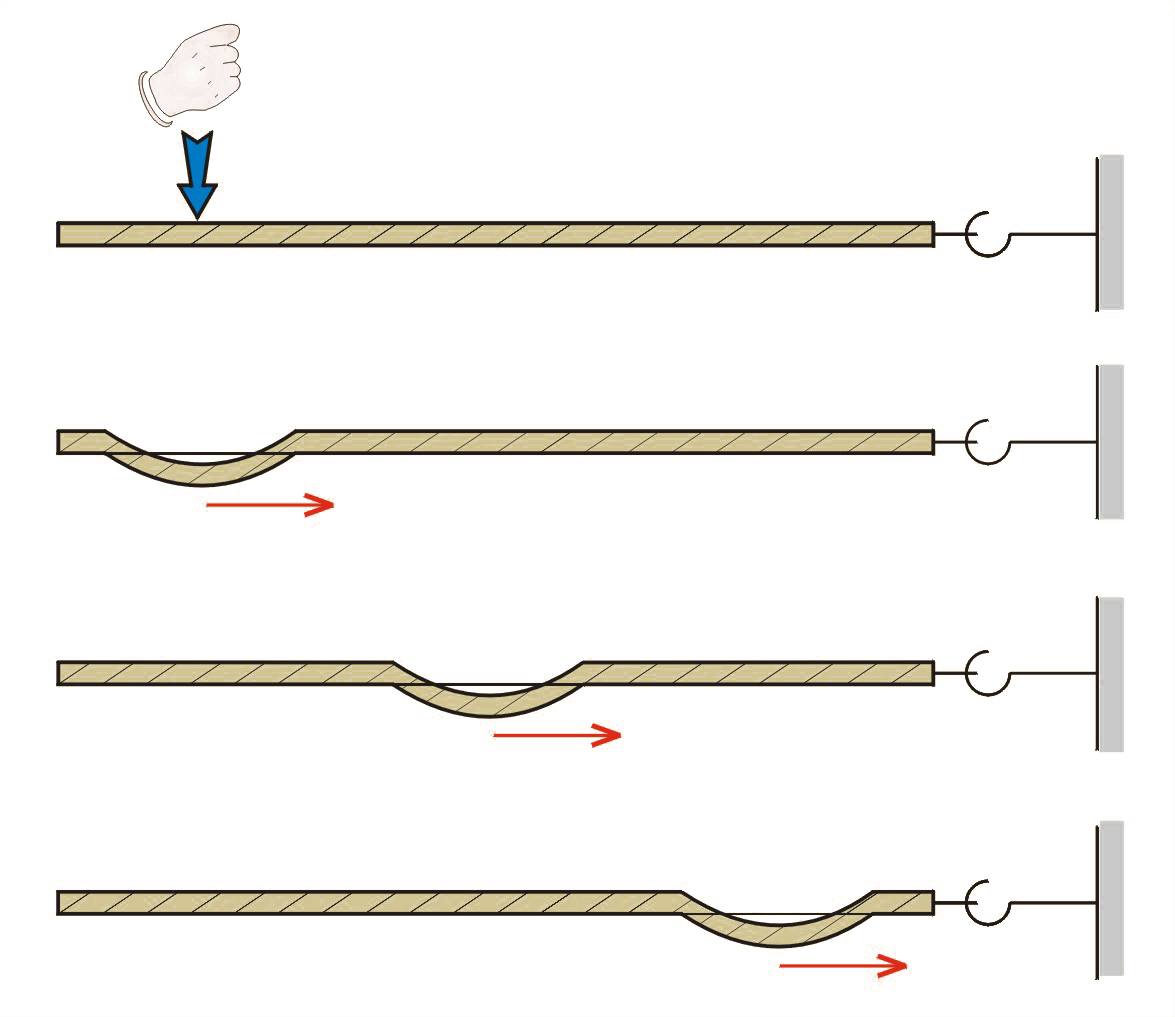
Z doświadczenia wyciągamy wniosek, że odkształcenie wywołane w ośrodku sprężystym (tutaj w sznurze) rozchodzi się w tym ośrodku. Mówimy, że przez sznur przebiega fala. Dlatego ruch falowy określamy jako przemieszczanie się odkształcenia w ośrodku, zaś rozchodzące się odkształcenie nazywamy falą.
Dlaczego odkształcenie nie pozostaje w spoczynku, lecz rozchodzi się w ośrodku w postaci fali? Otóż cząstka ośrodka sprężystego odchylona z położenia równowagi zaczyna drgać, a ponieważ jest ona powiązana siłami wiązania z sąsiednimi cząstkami, pobudza sąsiednią cząsteczkę do drgań. Ta pobudza następną sąsiednią itd. W ten sposób odkształcenie przemieszcza się na coraz większą odległość, czyli rozchodzi się w ośrodku. Mówimy, że w ośrodku występuje sprzężenie między jego elementami. To sprzężenie powoduje, że energia każdej cząstki zostaje przekazana cząstce następnej. Część energii zostaje też rozproszona. Jeśli więc nie dostarczamy kolejnych porcji energii (poprzez kolejne uderzenia), to cząstki ośrodka powrócą do swoich stanów równowagowych.
Dlaczego odkształcenie rozchodzi się w ośrodku nie „błyskawicznie”, ale z określoną prędkością? Widzieliśmy, że aby odkształcenie mogło przejść z jednego do drugiego końca sznura, musiał upłynąć określony czas. Występuje tu coś w rodzaju „sztafety”. Cząsteczki znajdują się w pewnej, chociaż małej, ale skończonej odległości od siebie. Jedna cząsteczka oddaje część swojej energii drugiej, ta z kolei następnej itd. Na przekazanie tej „pałeczki” potrzebny jest, choć krótki, ale skończony odcinek czasu, za każdym razem jednakowy. Stosunek wzajemnej odległości sąsiednich cząsteczek do tego elementarnego czasu przekazania energii jest właśnie prędkością (skończoną) fali.
Doświadczenie pokazowe 2
W tym doświadczeniu zastąpmy sznurek wężem gumowym (gumą pasmanteryjną czy innym materiałem elastycznym), który można mniej lub bardziej naprężyć. Przeprowadzając doświadczenie przy różnych naprężeniach ośrodka przekonamy się, że prędkość rozchodzenia się fali jest tym większa, im ośrodek jest bardziej naprężony. Wynika to przede wszystkim z faktu, że przy zwiększonym naprężeniu sąsiednie cząsteczki ośrodka są silniej ze sobą sprzężone (powiązane ze sobą), dzięki czemu szybciej przekazują sobie energię. Związek prędkości rozchodzenia się fali z naprężeniem ośrodka wykorzystuje się m.in. przy strojeniu gitar i innych instrumentów strunowych (patrz – fale stojące).
Kierunek rozchodzenia się odkształcenia w ośrodku nazywamy kierunkiem rozchodzenia się fali. Widzieliśmy podczas przeprowadzonego doświadczenia, że odkształcenie rozchodziło się wzdłuż sznura (od ręki do ściany). A jaki był kierunek drgań? Drgania cząsteczek sznura odbywały się z góry na dół i odwrotnie, tzn. prostopadle do kierunku rozchodzenia się fali. Mówimy, że mamy tu do czynienia z falą poprzeczną. Ogólnie, falę nazywamy falą poprzeczną, gdy drgania odbywają się prostopadle do kierunku jej rozchodzenia.
Nie zawsze tak jest. Inny skrajny przypadek występuje wtedy, gdy drgania odbywają się wzdłuż kierunku rozchodzenia się fali. Mamy wówczas do czynienia z falą podłużną. Możemy ją zaobserwować w kolejnym doświadczeniu.
Doświadczenie pokazowe 3
Uderzamy dłonią w jeden koniec zawieszonej na cienkich linkach długiej sprężyny. Obserwujemy, jak wywołane w ten sposób zagęszczenie zwojów sprężyny przemieszcza się wzdłuż tej sprężyny, z jednego jej końca na drugi.
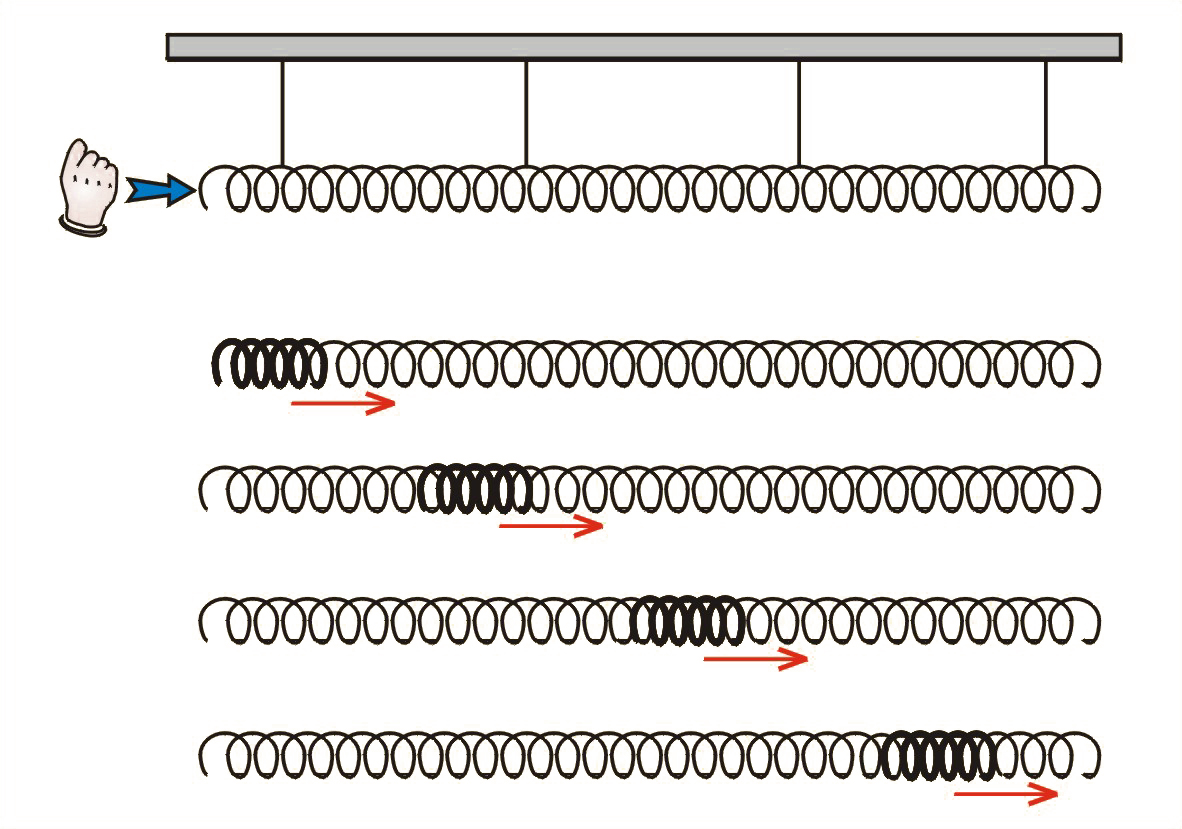
Fale głosowe (akustyczne) zaliczamy do fal podłużnych. Fala głosowa polega na rozchodzeniu się zagęszczeń i rozrzedzeń powietrza lub innego ośrodka – gazowego albo ciekłego.
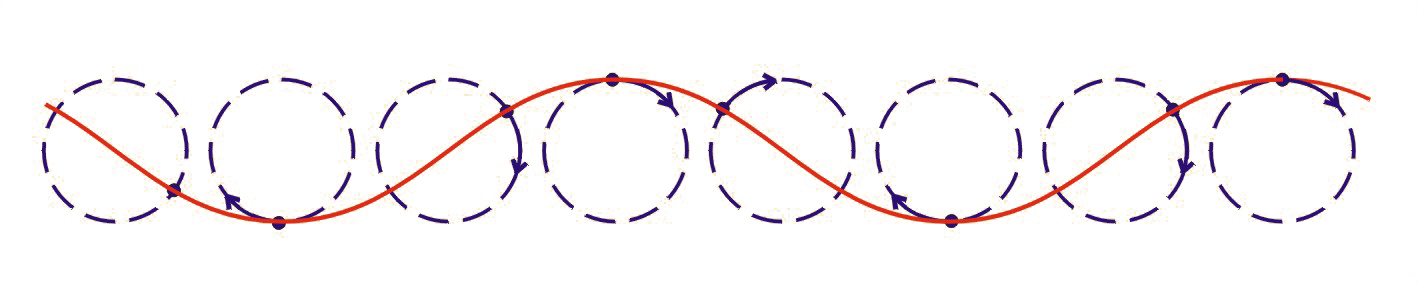
Przyjrzyjmy się jeszcze bardzo często spotykanym falom – falom na wodzie. Jeżeli spokojną powierzchnię wody zakłócimy, na przykład wrzucając kamień, to na powierzchni wody zacznie się rozchodzić fala. Z pozoru wydaje się, że jest to fala poprzeczna – taki bowiem ruch wykonuje powierzchnia wody. Jednakże bliższa analiza wykazuje, że cząsteczki wody wykonują w przybliżeniu ruchy kołowe (il. 5.18). Wobec tego taka fala nie jest ani poprzeczna, ani podłużna.
Przykład 5
W badaniach sejsmicznych drgań skorupy ziemskiej wykorzystuje się fakt, że fale podłużne rozchodzą się szybciej niż fale poprzeczne. Wiadomo, że prędkość fali podłużnej wynosi , zaś fali poprzecznej . Sejsmograf wykazał różnicę czasu między nadejściem fali podłużnej i poprzecznej. Znajdź odległość źródła trzęsienia ziemi od stacji sejsmicznej (przyjmij, że przy takiej wartości sejsmograf zarejestrował tylko fale, które rozchodziły się w skorupie ziemskiej oraz że można zaniedbać krzywiznę skorupy ziemskiej).
Rozwiązanie: Oznaczmy przez odległość między stacją sejsmiczną a centrum trzęsienia ziemi. Zatem:
oraz
Stąd:
oraz
więc:
Skąd:
Widzimy, że odległość centrum trzęsienia ziemi od stacji sejsmicznej wynosiła 1325 km.
Pytania i problemy
- Wyjaśnij, na czym polega ruch falowy. Podaj klasyfikacje fal oraz przykłady fal odpowiadających tej klasyfikacji.
- Scharakteryzuj falę poprzeczną i falę podłużną. Czy mogą istnieć takie fale, które nie są ani poprzeczne, ani podłużne?
- Z okna na drugim piętrze zwisa swobodnie gumowy wąż. Przy ziemi uderzono go, wysyłając ku górze poprzeczną falę. Czy fala ta porusza się jednostajnie, czy zwalnia albo przyspiesza? Uzasadnij swój wybór. Wskazówka: Zwróć uwagę na rozkład ciężaru w zwisającym pionowo wężu.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
