Pierwsze prawo Maxwella jest uogólnieniem prawa indukcji Faradaya.

Przyjrzyjmy się doświadczeniu przedstawionemu na il. 9.2. Przewodnik kołowy (pętla) i magnes zbliżają się do siebie z prędkością $v$. Spójrzmy na tę sytuację z dwóch układów odniesienia. W układzie $\left(x\text{'}y\text{'}z\text{'}\right)$, związanym z magnesem, pętla porusza się z prędkością $v$. Na elektrony w pętli, poruszające się wraz z nią w polu magnetycznym, działa siła Lorentza, która wprawia je w ruch okrężny. W ten sposób w pętli indukuje się prąd.

W układzie $\left(xyz\right)$, związanym z pętlą, średnia prędkość ładunków jest równa zeru, więc siła Lorentza też jest równa zeru, niemniej zbliżający się magnes wywołuje w pętli prąd. Jest to zrozumiałe, gdyż zgodnie z zasadą względności wszystkie zjawiska w układach inercjalnych przebiegają tak samo (również i przepływ prądu). Skoro prąd w pętli płynął w układzie $\left(x\text{'}y\text{'}z\text{'}\right)$, to musi również płynąć w układzie $\left(xyz\right)$. Liczy się tylko to, że pętla i magnes są względem siebie w ruchu!

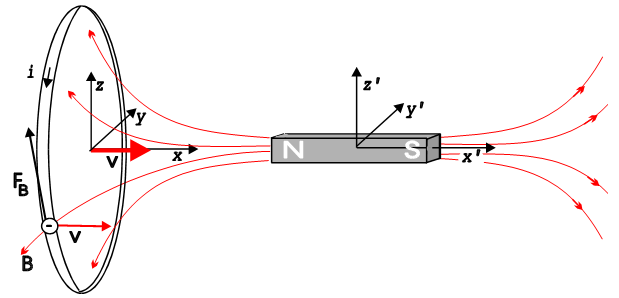
Zapytajmy zatem, jaka siła w układzie $\left(xyz\right)$ wywołuje prąd, skoro nie jest to siła Lorentza? Może to być jedynie siła elektryczna $F=qE$ przemieszczająca ładunki $q$ stanowiące prąd elektryczny. Zatem w układzie $\left(xyz\right)$ prąd jest wywołany polem elektrycznym o natężeniu $\overrightarrow{E}$ powstającym w obwodzie pod wpływem zbliżania się do niego magnesu. Wniosek ten jest całkowicie potwierdzony doświadczalnie, co opiszemy w dalszej części rozdziału.

Jakie cechy ma elektryczne pole indukcyjne wywołujące prąd w obwodzie przy zbliżaniu się magnesu (zbliżaniu się źródła pola magnetycznego)?

1. Zauważmy, że nie jest to takie pole, z jakim mieliśmy do czynienia w elektrostatyce, gdyż jego linie nie zaczynają się ani nie kończą na ładunkach elektrycznych (nie jest ono wywołane ładunkami elektrostatycznymi, czyli ładunki elektryczne nie są źródłami tego pola). Linie elektrycznego pola indukcyjnego zamykają się same w sobie. Dlatego pole to nosi nazwę pola wirowego.
2. Siła elektryczna (styczna do toru), przemieszczająca w pętli ładunek $q$, wykonuje pracę. Na małym odcinku drogi $\Delta l$ jest to praca $\Delta W=F\Delta l=qE\Delta l$, a przy pełnym obiegu:
   $$W=q\sum _{\text{po drodze zamkniętej}}\overrightarrow{E}\cdot \Delta \overrightarrow{l}$$

   ( 9.1 )

Przypomnijmy sobie, że pole, w którym praca zależy od drogi, nie jest polem zachowawczym. Zatem elektryczne pole indukcyjne nie jest polem zachowawczym.

Powróćmy do doświadczenia przedstawionego na il. 9.2. Stwierdziliśmy, że na skutek zmiennego strumienia pola magnetycznego przepływającego przez pętlę powstaje w niej wirowe pole elektryczne, które przy każdym obiegu pętli wykonuje pracę $W$ przemieszczenia ładunków równą przemieszczanemu ładunkowi pomnożonemu przez cyrkulację wektora $\overrightarrow{E}$ indukowanego pola elektrycznego (suma po drodze zamkniętej $\sum \overrightarrow{E}\cdot \Delta \overrightarrow{l}$, występująca w równaniu (9.1), nazywa się cyrkulacją wektora $\overrightarrow{E}$). Pracę tę identyfikujemy z pracą siły elektromotorycznej indukcji $E_{\mathrm{ind}}$ – patrz wzór (3.16). Z drugiej strony, zgodnie z definicją SEM, $E=\frac{W}{q}$. Zatem, stosując wzór (4.6), otrzymamy:

Wzór powyższy w ogólnej postaci wyraża treść pierwszego prawa Maxwella. Słowami można to wyrazić następująco:

Należy zwrócić uwagę na to, że prawo Maxwella wyrażone za pomocą wzoru (9.2) jest ogólniejsze od prawa indukcji Faradaya. W treści prawa Maxwella abstrahuje się od obecności przewodnika w zmiennym polu magnetycznym. Prawo to mówi, że niezależnie od tego, czy występuje obwód elektryczny, czy mamy do czynienia z próżnią, zawsze zmienne pole magnetyczne spowoduje wywołanie wirowego pola elektrycznego. Występowanie wirowego pola elektrycznego w obecności przewodnika zamanifestuje się wystąpieniem indukowanego prądu, o którym mówimy, że jest wywołany przez SEM indukcji.

Najprostszą ilustracją doświadczalnego potwierdzenia prawa Maxwella jest urządzenie do przyspieszania elektronów w zmiennym polu magnetycznym – tzw. betatron – omówiony w poniższym przykładzie.

Przykład „Betatron”

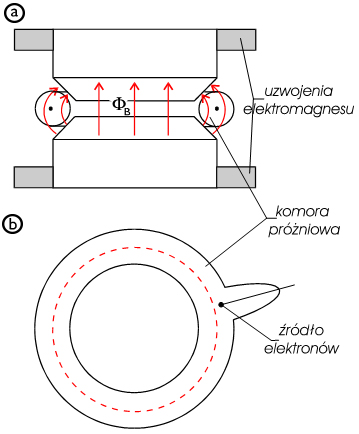
Na il. 9.3 przedstawiony jest schemat betatronu – akceleratora elektronów. Przez uzwojenia elektromagnesu przepływa zmienny prąd elektryczny (narastający impulsowo) wytwarzający zmienny strumień pola magnetycznego między nabiegunnikami elektromagnesu, gdzie znajduje się komora próżniowa w kształcie torusa (obwarzanka), do której wstrzykuje się elektrony. Jak wiemy, zmienne pole magnetyczne wytwarza wirowe pole elektryczne, które działa na elektrony siłą $F_e=eE$ i przyspiesza je. Po każdym obiegu okręgu elektrony nabywają coraz to większej prędkości. Jest to wyraźny dowód na słuszność pierwszego prawa Maxwella – w torusie panuje próżnia, nie ma żadnego przewodnika, w którym mogłaby powstać siła elektromotoryczna indukcji, niemniej jednak elektrony są przyspieszane. Mogą być one przyspieszane tylko dzięki wirowemu polu elektrycznemu indukowanemu w próżni torusa przez zmienne pole magnetyczne.

Elektromagnes, oprócz przyśpieszania elektronów, pełni jeszcze inną funkcję: na skutek działania siły Lorentza ${\overrightarrow{F}}_B=e\cdot \overrightarrow{v}\times \overrightarrow{B}$, prostopadłej do kierunku ich prędkości, zakrzywia ich tor (siła ta jest siłą dośrodkową).

Maksymalna energia elektronów obiegających setki tysięcy razy orbity kołowe w betatronie przekracza 100 MeV (przypomnijmy, że 1 eV jest to energia, jaką uzyskuje elektron przy przejściu różnicy potencjałów 1 V, $1\text{eV}=\mathrm{1,6}\cdot {10}^{-19}\text{J}$). Elektrony przy tej energii osiągają prędkości wynoszące $\mathrm{0,999}986c$, gdzie $c$ jest prędkością światła w próżni. Dlatego musimy tu stosować relatywistyczne prawa ruchu. Ograniczenie energii elektronów w betatronie wynika głównie z tego, że – przyspieszane – tracą one energię na wypromieniowanie fal elektromagnetycznych.

W celu osiągnięcia jeszcze wyższych energii cząstek stosuje się obecnie akceleratory oparte na trochę innej zasadzie, niewymagającej stosowania pełnych elektromagnesów.

Pytania i problemy

1. Jakie znaczenie teoretyczne w nauce i jakie konsekwencje praktyczne ma teoria Maxwella?
2. Podaj pierwsze prawo Maxwella oraz zapisz je w postaci wzoru. Jaki ma ono związek z prawem indukcji Faradaya?
3. Jakie cechy ma pole elektryczne indukowane przez zmienne pole magnetyczne? Podaj podobieństwa i różnice tego pola i pola elektrostatycznego.