Zanim bliżej omówimy interferencję, czyli nakładanie się fal, podamy zasadę superpozycji fal. W tym celu przeprowadźmy poniższe doświadczenie.

Doświadczenie pokazowe 1

Dotknij jednocześnie dwoma ostrymi prętami powierzchni wody. Z obu miejsc styku prętów z wodą rozejdą się dwa kręgi, które przejdą przez siebie. Jedna fala przejdzie przez drugą, jak gdyby tamta nie istniała.

Wyciągamy wniosek, że fale nie oddziałują ze sobą, ale rozchodzą się niezależnie jedna od drugiej.

Jeżeli dwie fale (lub więcej) o tej samej długości spotykają się w określonym miejscu, to pobudzają tam cząstkę do drgań – każda z osobna, niezależnie od siebie (ponieważ fale nie oddziałują ze sobą). Wychylenie cząstki ośrodka jest sumą wychyleń wynikających z drgań fal pochodzących z różnych źródeł. Jest to treść zasady superpozycji.

Następne doświadczenie pokaże nam interferencyjny obraz fal na wodzie.

Doświadczenie pokazowe 2

Za pomocą dwóch ostrzy połączonych ze sobą w postaci widełek pobudzamy wodę do drgań w dwóch miejscach jednocześnie. Zaobserwujemy, że w wyniku nakładania się fal rozchodzących się z dwóch źródeł powstaną smugi – w których nie występuje drganie cząsteczek wody – na przemian z obszarami, których woda faluje ze zdwojoną intensywnością (il. 5.28).

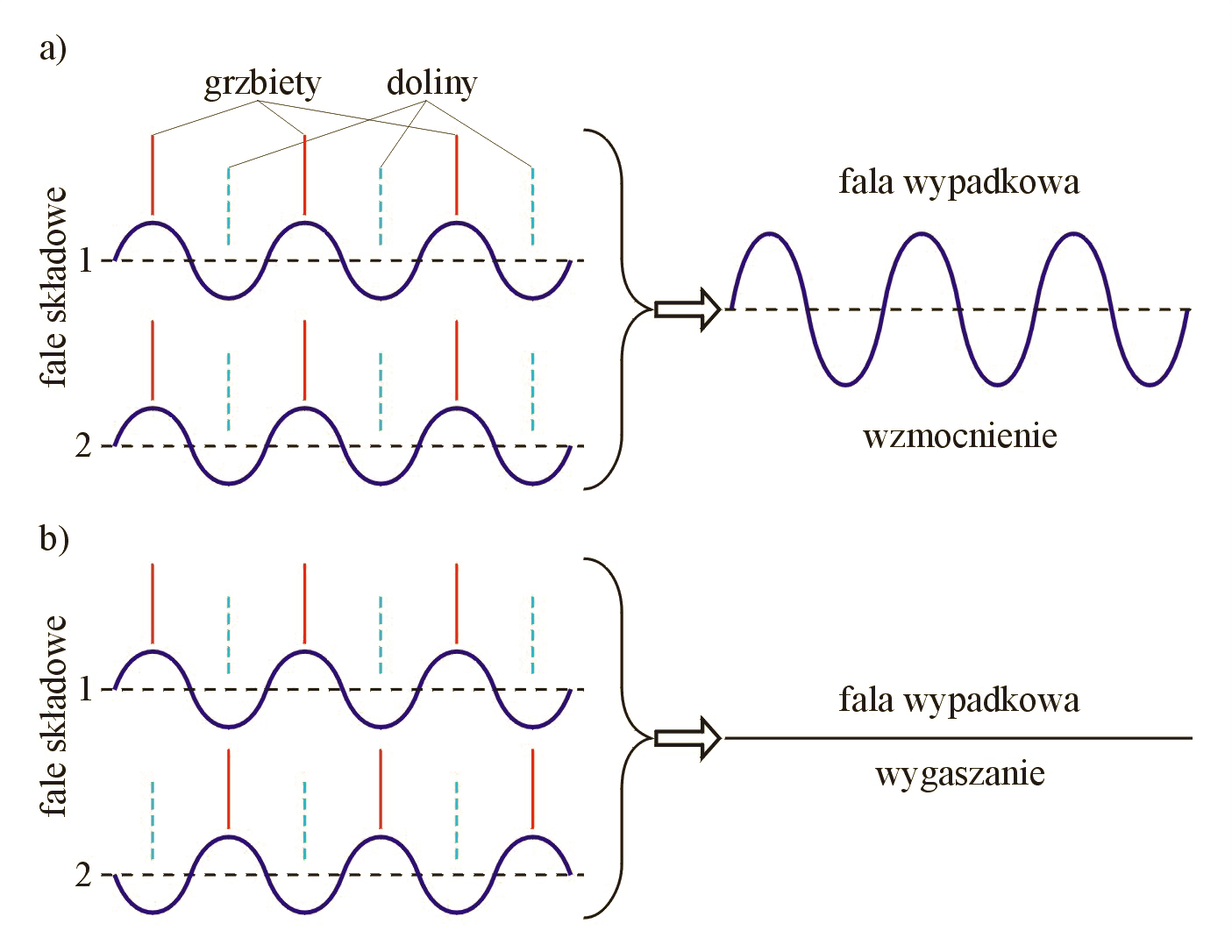
Obecnie spróbujemy zrozumieć, dlaczego przy interferencji powstaje taki właśnie rozkład fal. Weźmy pod uwagę najpierw sytuację prostszą, gdy nakładają się dwie fale (il. 5.29). Jeżeli dwie fale w miejscu spotkania, np. w punkcie $P$, mają fazy zgodne, tzn. grzbiety jednej fali spotykają się jednocześnie z grzbietami drugiej, wtedy i doliny jednej fali spotykają się jednocześnie z dolinami drugiej fali – w takim punkcie następuje interferencyjne wzmocnienie fali (il. 5.29a). Jeżeli sytuacja jest taka, jak na il. 5.29b, gdzie fale spotykają się w przeciwfazie (tzn. grzbiety jednej fali spotykają się z dolinami drugiej i na odwrót) to w takim punkcie następuje interferencyjne wygaszenie fali.

Na il. 5.28 przedstawiono obraz interferencyjny fal kulistych wychodzących z dwóch szczelin, ujęty w jednej określonej chwili. Podobnie jest na schematycznym rysunku na il. 5.30, na którym grzbiety fal zaznaczono linią ciągłą, doliny zaś – linią przerywaną. Widzimy, że miejsca spotkań grzbietów dwóch fal oraz miejsca, w których spotykają się ich doliny, układają się wzdłuż określonych linii. Wzdłuż tych linii następuje wzmocnienie fal. Miejsca spotkań grzbietów jednej fali z dolinami drugiej fal (tam występuje wygaszenie) układają się wzdłuż linii prostych naprzemiennie z liniami wzmocnień.

Obecnie opiszemy to zjawisko ściślej, za pomocą języka matematyki. Najpierw zauważmy, że aby mógł powstać stabilny obraz interferencyjny, fale składowe muszą mieć jednakową częstość $\omega$ i stałą różnicę faz. Fale o tej samej częstości rozchodzące się w tym samym ośrodku będą miały również jednakowe długości $\lambda$ i jednakowe liczby falowe $k$.

Załóżmy, że w odległości $l$ od przesłony z dwiema szczelinami znajduje się ekran (il. 5.31). Załóżmy dodatkowo, że natężenia $I_1$ oraz $I_2$ tych fal są w każdym punkcie ekranu jednakowe (w rzeczywistości tak nie jest, ze względu na różnice odległości od szczelin); oznaczymy to wspólne natężenie przez $I_0$.

Fale dochodzące do różnych punktów $P$ ekranu będą tam interferować. Zajmiemy się dwiema skrajnymi sytuacjami: pełnego wzmocnienia i pełnego wygaszenia interferencyjnego. Wystąpienie na ekranie jednego z tych przypadków zależy od różnicy odległości źródeł fal (szczelin) od interesującego nas punktu $P$ na ekranie $\Delta r=r_2-r_1$ (nazywa się ją różnicą dróg). Oczywiście, ta różnica dróg jest zależna od położenia punktu $P$ na osi $y$ lub od kąta $\alpha$, gdyż – jak widać na rysunku – w przybliżeniu $\Delta r=r_2-r_1=dsin\alpha$ (to przybliżenie jest słuszne gdy $l$ jest dużo większe od $d$). Zatem natężenie drgania wypadkowego na ekranie $E$ będzie się zmieniać wraz z kątem $\alpha$ (i również – wraz z wartością $y$) okresowo, jak na il. 5.31.

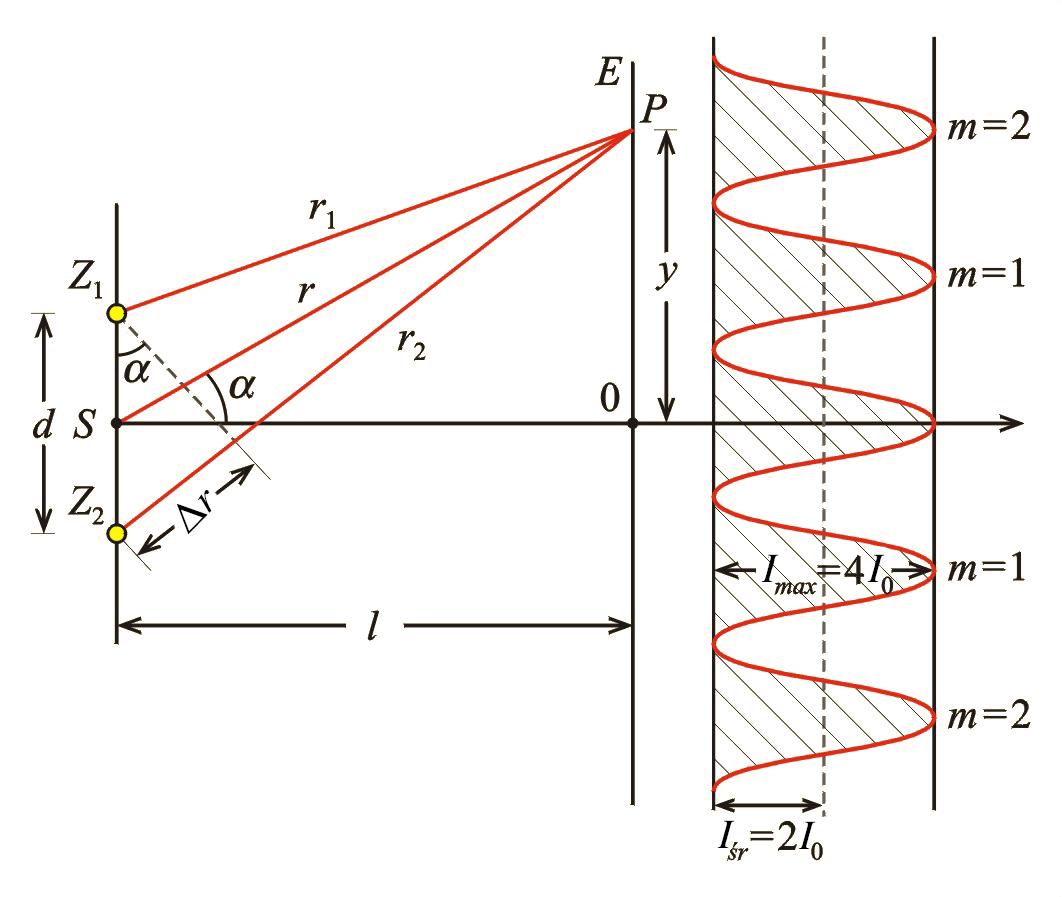
Natężenie wypadkowe osiąga maksimum w tych miejscach, gdzie różnica dróg jest równa parzystej wielokrotności połowy długości fali, tzn.

gdzie $m$ jest dowolną liczbą całkowitą. Tam powstanie interferencyjne maksimum.

Natężenie wypadkowe jest minimalne w tych miejscach, gdzie różnica dróg jest równa nieparzystej wielokrotności połowy długości fali, tzn.

gdzie $m$ jest dowolną liczbą całkowitą.

W skrócie warunki na maksimum i minimum interferencyjne można zapisać następująco:

W przypadku skrajnego wzmocnienia interferencyjnego amplituda wypadkowej fali jest sumą amplitud interferujących fal. W punktach spełniających warunek (5.51) następuje więc podwojenie amplitudy, co prowadzi do czterokrotnego wzrostu natężenia fali. Jest to zgodne z kwadratową zależnością natężenia od amplitudy – wzór (5.50). Z kolei w przypadku pełnego wygaszenia interferencyjnego amplituda wypadkowej fali jest różnicą amplitud interferujących fal. W punktach spełniających warunek (5.52) amplituda wypadkowa wynosi więc zero. Skutkiem jest zerowe natężenie, także zgodnie ze wzorem (5.50).

Przy interferencji następuje przegrupowanie energii – energia przechodzi z miejsc minimalnego natężenia do miejsc z maksimami natężenia. Zgodnie z zasadą zachowania energii, średnie natężenie (il. 5.31) jest równe sumie natężeń obu fal: $I_{śr}=2I_0=I_1+I_2$.

Interferencja jest zjawiskiem typowo falowym (podobnie jak dyfrakcja). Jeżeli nie znamy natury jakiegoś promieniowania, ale możemy wykazać doświadczalnie, że promieniowanie to podlega interferencji, to możemy twierdzić, że mamy do czynienia z falą. W ten sposób udowodniono na przykład, że światło ma naturę falową.

Pytania i problemy

1. Na czym polegają zjawiska interferencji i dyfrakcji fali?
2. Jaki warunek musi spełniać różnica dróg fal, aby wystąpiło: a) maksimum interferencyjne fali wypadkowej, b) minimum interferencyjne fali wypadkowej? Wyjaśnij mechanizm powstawania minimum i maksimum.
3. Podaj treść zasady superpozycji fal.
4. Dwa źródła, $Z_1$ i $Z_2$, odległe o $d$, emitują fale o jednakowych długościach $\lambda =\frac{1}{2}d$. Źródła te leżą na końcach średnicy okręgu o środku $O$. Wskaż wszystkie punkty na okręgu, w których występuje wzmocnienie interferencyjne tych fal.