3.7. Pole magnetyczne solenoidu

W celu wyznaczenia pola magnetycznego solenoidu założymy, że pole magnetyczne występuje tylko wewnątrz długiego solenoidu, a na zewnątrz jest równe zeru. Teoretyczne uzasadnienie tego zjawiska znajdziemy w tym rozdziale (to przybliżenie jest tym dokładniejsze, im długość solenoidu jest większa w porównaniu z jego średnicą).

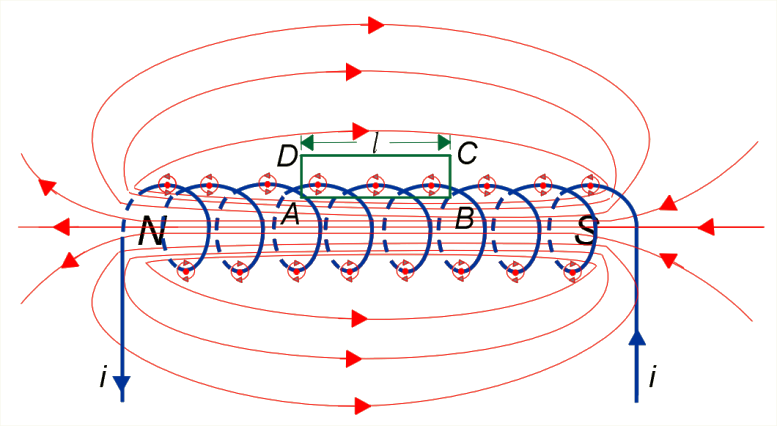
Wykorzystamy prawo Ampère'a. Obierzmy drogę cyrkulacji wektora $\vec{B}$ w postaci prostokąta $A B C D$ , jak na il. 3.30. Cyrkulacja wektora $\vec{B}$ po tej drodze wyniesie $B l$ , ponieważ tylko na odcinku $A B$ iloczyn skalarny $\vec{B}\cdot\Delta\vec{l}$ nie znika. Przez powierzchnię rozpiętą na prostokącie $A B C D$ przepływa prąd o całkowitym natężeniu $N I$ $(N$ – liczba zwojów na odcinku $l)$ , więc zgodnie z prawem Ampère'a $Bl=\mu_{0}NI$ . Stąd wzór na indukcję magnetyczną solenoidu:

B=\frac{\mu_{0}NI}{l}=\mu_{0}nI

( 3.31 )

gdzie $n=\frac{N}{l}$ jest liniową gęstością zwojów w solenoidzie.

Ilustracja 3.30. **Prostokątna droga cyrkulacji wektora $\vec{B}$ obrana dla zastosowania prawa Ampère'a**

Pierścień Rowlanda

Pokażemy teraz inny sposób otrzymania tego wzoru, wykorzystując tzw. pierścień Rowlanda. Jest to spirala nawinięta na toroidalny rdzeń, czyli solenoid mający kształt obwarzanka, który w przekroju przedstawiony jest na il. 3.31.

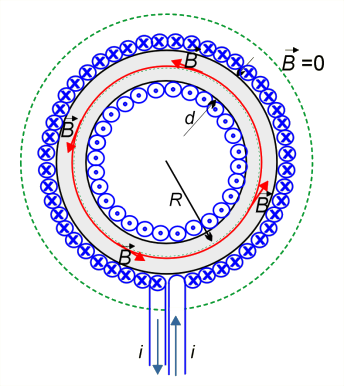
Ilustracja 3.31. **Pole magnetyczne spirali nawiniętej na torusie**

Zastosujemy prawo Ampère'a (3.23). Symetria układu narzuca koncentryczne linie pola magnetycznego. Wartość wektora $\vec{B}$ w każdym punkcie takiej linii jest taka sama. Cyrkulacja indukcji $\vec{B}$ po drodze kołowej o promieniu $R$ wewnątrz toroidu wyniesie $2\pi RB$ . Przez powierzchnię rozpiętą na tej drodze kołowej przepływa całkowity prąd równy $N I$ , gdzie $N$ jest liczbą zwojów. Zatem, zgodnie z (3.23), mamy: $2\pi RB=\mu_{0}nI$ , więc wzór na indukcję toroidu przybierze postać:

B=\frac{\mu_{0}NI}{2\pi R}

( 3.32 )

Z prawa Ampère'a wynika, że na zewnątrz toroidu nie ma pola magnetycznego. Przez powierzchnię (np. koło) rozpiętą na okręgu o promieniu $r$ większym od zewnętrznego promienia toroidu $R_{z}$ przepływa sumaryczny prąd o natężeniu równym zeru (każdy zwój przechodzi przez tę powierzchnię dwa razy, a prąd w obu częściach zwoju przepływa przez tę powierzchnię w przeciwnych kierunkach). Z kolei przez koło o promieniu $r$ mniejszym od wewnętrznego promienia toroidu $R_{w}$ nie przepływa żaden prąd. W związku z tym w obu przypadkach prawa strona równania Ampère'a jest równa zeru, więc cyrkulacja wektora $\vec{B}$ musi być również zerowa, stąd $B=0$ .

Solenoid można utworzyć przez „wyprostowanie” toroidalnej zwojnicy. Zatem pole magnetyczne wewnątrz długiego solenoidu nie powinno się prawie wcale różnić od pola toroidu (o dużej średnicy) o tej samej gęstości zwojów, jeżeli płynie przez nie prąd o takim samym natężeniu $I$ . Długość $l$ solenoidu odpowiada obwodowi toroidu, $l=2\pi R$ , dlatego, wykorzystując wzór (3.32), otrzymamy wzór (3.31).

Jak widzieliśmy, pole magnetyczne występuje tylko wewnątrz toroidu, stąd argument przemawiający za tym, że pole magnetyczne także występuje tylko wewnątrz długiego solenoidu, a na zewnątrz jest znikome.

Przykład 7

Na kartonową rurkę o promieniu $r=1\, cm$ nawinięto (ciasno) $N=1\,000$ zwojów miedzianego przewodu o średnicy $d=0,2\, mm$ . Średnica przewodu wraz z izolacją wynosi $d\text{’}=0,3\, mm$ . Tak uzyskany solenoid zasilono napięciem $U$ . Oblicz napięcie $U$ , wiedząc, że wewnątrz solenoidu indukcja pola magnetycznego wynosi $B=10^{-3}\, T$ , czyli jest ono około 20 razy silniejsze niż ziemskie pole magnetyczne. Oporność właściwa miedzi $\rho=1,6\,\Omega\cdot m$ .

Rozwiązanie: Użyte napięcie wyznaczymy z prawa Ohma:

U=I R

( 3.33 )

Natężenie prądu $I$ niezbędne do wytworzenia pola $B$ o żądanej indukcji wyznaczymy ze wzoru (3.31), który po przekształceniu przybiera postać:

I=\frac{B l}{\mu_{0} N}=\frac{B d' N}{\mu_{0} N}=\frac{B d'}{\mu_{0}}

( 3.34 )

Po podstawieniu danych obliczamy $I\approx0,24\, A$ .

Opór elektryczny $R$ nawiniętego przewodu wyznaczymy ze wzoru (2.10):

R=\rho\frac{L}{S}=\rho\frac{N\cdot2\pi r}{\frac{1}{4}\pi d^{2}}=\frac{8\rho N r}{d^{2}}

( 3.35 )

Po podstawieniu danych obliczamy $R=32\,\Omega$ .

Przyjęcie we wzorze (3.35), że długość przewodu

L=N\cdot2\pi r

, jest przybliżeniem. W rzeczywistości, nawinięcie jednego zwoju wymaga użycia przewodu o długości nieco większej od

2\pi r

– jest to związane z faktem, że po wykonaniu przewodem jednego obiegu walca jego koniec nie trafia w punkt wyjścia. Należałoby tu zastosować twierdzenie Pitagorasa:

L=N\sqrt{\left(2\pi r\right)^{2}+s^{2}}

Ze względu jednak na fakt, że $s$ jest ponad 20 razy mniejsze od $2\pi r$ , zastosowane przybliżenie jest uzasadnione.

Ostatecznie obliczamy niezbędne napięcie $U=7,68\, V$ .

Zwróćmy uwagę, że w zaprojektowanym solenoidzie będzie się wydzielała moc $P=UI\thickapprox1,8\, W$ . Jest to na pozór niewielka moc, ale może ona spowodować zauważalne podgrzanie bardzo cienkiego, zaizolowanego przewodu.

Pytania i problemy

Korzystając z prawa Ampère'a, wyprowadź związek między indukcją pola magnetycznego i natężeniem prądu w nieskończenie długim prostoliniowym przewodniku.
Wyjaśnij, dlaczego na zewnątrz pierścienia Rowlanda nie występuje pole magnetyczne, mimo że w zwojnicy tego pierścienia płynie prąd.
Wytłumacz, dlaczego wewnątrz pierścienia Rowlanda występuje pole magnetyczne, gdy w zwojnicy tego pierścienia płynie prąd.
Na il. 3.30 przedstawiono linie pola magnetycznego solenoidu z prądem. Gęstość linii jest większa tam, gdzie pole jest silniejsze. Uzasadnij przebieg linii pola, korzystając z prawa Ampère'a dla pierścienia Rowlanda.