2.4. Doświadczenie „Ohm”
Nasze doświadczenie ma wykazać, że prawo Ohma (wzór (2.9)) jest spełnione w rzeczywistości. Dodatkowym jego efektem będzie wyznaczenie oporu elektrycznego badanego przewodnika.
Z kawałka drutu oporowego (np. długości 0,6 m i średnicy 0,5 mm) zwijamy spiralę tak, aby jej poszczególne zwoje nie zwierały się ze sobą (przewodnik kształtujemy w spiralę dla wygody, aby nie zajmował dużo miejsca).
Jeżeli w szkole jest regulowany zasilacz prądu stałego, to końce spirali podłączamy do niego przez amperomierz, dołączając do nich woltomierz, według schematu przedstawionego na il. 2.4a. Jeżeli takiego zasilacza nie ma, budujemy go sami z kilku ogniw. Dobrym pomysłem jest użycie trzech baterii, tzw. płaskich (3R12), każda o nominalnej SEM 4,5 V. Taka bateria składa się z trzech półtorawoltowych ogniw. Baterie łączymy w szereg i odsłaniamy przewody łączące ogniwa każdej baterii, jak na il. 2.4b (Uwaga: Nie należy wyjmować ogniw z baterii – może to spowodować wyciek elektrolitu, który jest substancją żrącą i niebezpieczną dla zdrowia). W ten sposób, podłączając jeden przewód do jednej elektrody, a drugi kolejno do poszczególnych odsłoniętych złączy ogniw, będziemy dysponować SEM o różnych wartościach.
W obwodzie warto zastosować wyłącznik, by niepotrzebnie nie wyczerpywać baterii i nie podgrzewać badanego opornika, którego opór mógłby znacząco zmienić się pod wpływem wydzielanego w nim ciepła.

Ustawiamy SEM źródła na najniższą wartość, np. 1,5 V. Mierzymy napięcie na oporniku i natężenie prądu . Powtarzamy te czynności dla różnych wartości SEM, np. 1,5 V, 3 V, 4,5 V itd.
Wyniki pomiarów zapisujemy w tabelce przygotowanej według wzoru (il. 2.5).

Dane z tabeli nanosimy na wykres zależności od w postaci punktów. Zanim poprowadzimy prostą między tymi punktami, naniesiemy na wykres prostokąty niepewności pomiarowych.
Przeprowadzamy dyskusję niepewności pomiarowych według zasad podanych w tomie I, rozdz. 1.D1 Ocena dokładności wyników pomiarów (Dodatek). Najpierw ocenimy niepewności pomiarów bezpośrednich: napięcia i . Możemy przyjąć, że niepewność pomiaru to połowa wartości najmniejszej działki przyrządu pomiarowego oraz wartość wynikająca z tzw. klasy przyrządu pomiarowego. W elektrycznych przyrządach pomiarowych klasę podaje się zwykle jako liczbę umieszczoną z boku na skali, np. „1”, „2,5”. Liczba ta oznacza maksymalną niepewność pomiarową w procentach zakresu skali, na którym pracujemy. Ta informacja, wraz z oszacowaniem połowy działki na skali, pozwala nam ocenić niepewność pomiaru. Na przykład, pracujemy na zakresie skali 10 V, przy klasie 1. Oznacza to, że część niepewności pomiaru napięcia wynikająca z klasy przyrządu wynosi , niezależnie od wartości aktualnego odczytu na tym zakresie; np. zarówno przy odczycie 6 V, jak i 4,5 V niepewność pomiaru wynosi 0,1 V. Ocenione wartości wpisujemy do tabelki pomiarów. Więcej szczegółów dotyczących niepewności pomiarowych wielkości elektrycznych znajdziesz w rozdziale 2.9. Pomiary wielkości elektrycznych.
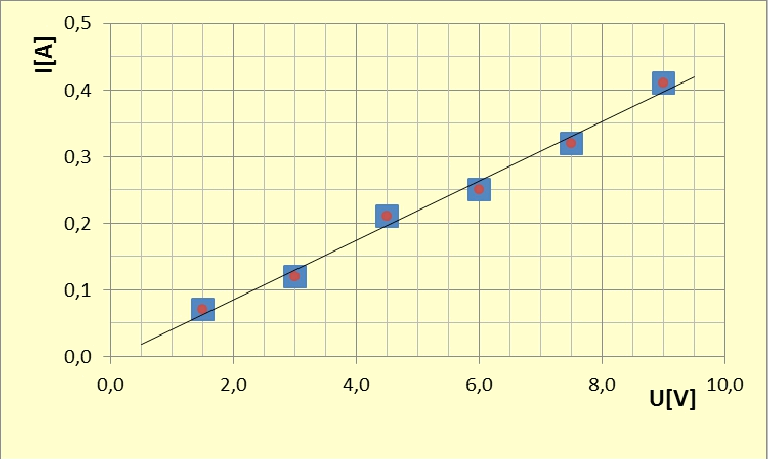
Przerywamy więc dyskusję dotyczącą niepewności pomiarowych i wracamy do wykresu. Każdy punkt pomiarowy na wykresie otaczamy prostokątem niepewności pomiarowych. Przykładowy wykres znajduje się na il. 2.6. Następnie sprawdzamy, przykładając linijkę, czy punkty pomiarowe układają się wzdłuż linii prostej. Jeżeli tak jest, to optymalną prostą prowadzimy tak, by przechodziła przez wszystkie prostokąty, jak najbliżej wszystkich punktów pomiarowych.
Możliwość przeprowadzenia prostej w pobliżu punktów pomiarowych świadczy o tym, że w naszym doświadczeniu występuje zależność proporcjonalna między natężeniem prądu a napięciem na badanym przewodniku. Tak interpretujemy prawo Ohma (wzór (2.9)):
Zatem sprawdziliśmy prawo Ohma w praktyce!
Nasze dane pomiarowe pozwalają wyznaczyć opór badanego przewodnika, który zgodnie z prawem Ohma wynosi . Zastosujemy metodę poznaną przy okazji doświadczenia Akceleracja (rozdział 1.13. Doświadczenie „Akceleracja”, tom II) i Akceleracja-BIS (rozdział 4.9. Doświadczenie „Akceleracja BIS”, tom II). Wartość uzyskamy, obliczając nachylenie wykresu , na podstawie dwóch dowolnie wybranych punktów na prostej optymalnej (najlepiej jest wybrać dwa punkty odległe od siebie). Należy jednak pamiętać, że nachylenie tego wykresu jest odwrotnością oporu . Prawo Ohma pokazuje, że jest proporcjonalne do , a współczynnikiem proporcjonalności jest wyrażenie .
Niepewność pomiaru oszacujemy na podstawie nachylenia dwóch prostych skrajnych. Jedna z nich ma nachylenie możliwe małe, druga – możliwie duże, ale obie przechodzą przez wszystkie prostokąty niepewności pomiarowej. Nachylenie pierwszej prostej pozwala wyznaczyć maksymalną dopuszczalną wartość oporu (opór elektryczny jest bowiem odwrotnością nachylenia). Analogicznie, nachylenie drugiej prostej skrajnej pozwala obliczyć opór . Jako maksymalną niepewność przyjmiemy połowę różnicy między i :
Stosując prawidłowe zaokrąglenia (patrz tom I, rozdz. 1.D1 Ocena dokładności wyników pomiarów (Dodatek)), zapisujemy nasz wynik końcowy z uwzględnieniem niepewności pomiarowej, np.
Pytania i problemy
- Znane są tzw. nieliniowe elementy obwodu, dla których wykres zależności
nie jest linią prostą lecz linią krzywą. Przykładami takich elementów
są opór żarówki, dioda prostownicza i termistor. Mówimy w takiej sytuacji,
że opór elektryczny takiego elementu zmienia się w trakcie badania.
Zbadano charakterystyki prądowo-napięciowe dwóch elementów nieliniowych „a” i „b” i uzyskano następujące wykresy (il. 2.8):
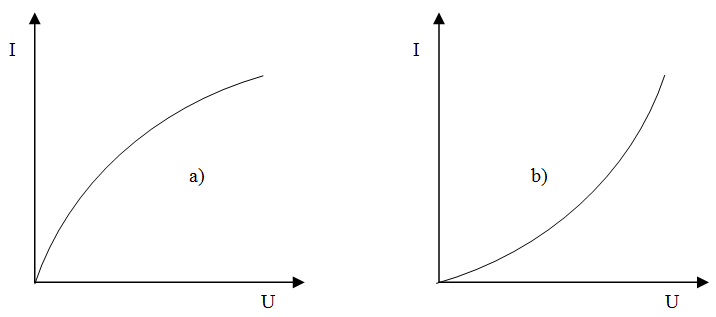 Ilustracja 2.8. Ilustracja do zadania
Ilustracja 2.8. Ilustracja do zadaniaRozstrzygnij, odpowiednio uzasadniając, jak zmieniał się, wraz ze wzrastającym napięciem, opór elektryczny elementu „a”, a jak – opór elementu „b”.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
