3.5. Prawo Ampère'a

Już po raz drugi pada nazwisko Ampère'a. Jego prawo, które teraz będziemy omawiać, jest – łącznie z uogólnieniem dokonanym później przez Maxwella – jednym z podstawowych praw elektromagnetyzmu. Prawo Ampère'a pozwala znajdować wektor indukcji $\vec{B}$ pola magnetycznego o określonej symetrii. Pole magnetyczne wytworzone przez nieskończenie długi prostoliniowy przewodnik z prądem jest polem kołowym tzn. takim, którego linie sił układają się we współśrodkowe okręgi.

Na il. 3.26a widoczne są koncentryczne, kołowe linie pola magnetycznego otaczające przewodnik z prądem. Wnioskujemy więc, że wektor indukcji magnetycznej $\vec{B}$ jest skierowany stycznie do okręgu w każdym jego punkcie. Z symetrii narzuconej przez prostoliniowy przewodnik z prądem, będący osią symetrii tego pola magnetycznego, możemy wywnioskować, że wartość wektora indukcji musi być jednakowa dla wszystkich punktów koncentrycznej linii pola otaczającej przewodnik (gdyż przestrzeń w tych miejscach ma te same własności). Jednakże na podstawie tych informacji nie możemy jeszcze wyznaczyć tej wartości. Aby się dowiedzieć czegoś więcej o wartości wektora indukcji, można zmierzyć siłę Lorentza w różnych odległościach od przewodnika i doświadczalnie ustalić względną zależność indukcji $\vec{B}$ od odległości $r$ , dla różnych wartości natężenia prądu $I$ płynącego przez przewodnik. Doświadczenie daje możność ustalenia następującej proporcji:

B\sim\frac{I}{r}

( 3.19 )

Po podstawieniu współczynnika proporcjonalności w postaci $\frac{\mu_{0}}{2\pi}$ $\mu_{0}$ nazywamy przenikalnością magnetyczną próżni), otrzymamy:

B=\frac{\mu_{0}I}{2\pi r}

( 3.20 )

Wzór ten po przekształceniu przyjmie postać:

B\cdot2\pi r=\mu_{0}I

( 3.21 )

Lewa strona wzoru (3.21) ma znaczenie tzw. cyrkulacji wektora indukcji $\vec{B}$ . W tym szczególnym przypadku cyrkulacja to nic innego, jak iloczyn stałej wartości $\vec{B}$ wektora $\vec{B}$ stycznego do okręgu otaczającego (współosiowo) prostoliniowy przewodnik z prądem i długości obwodu tego okręgu.

Cyrkulacja jest bardzo użytecznym pojęciem. W dowolnym przypadku pola magnetycznego definiuje się ją następująco. W polu magnetycznym wyznaczamy zamkniętą drogę, jak na il. 3.26a i il. 3.26b. Drogę tę dzielimy na bardzo małe elementy (przemieszczenia) o długości $\Delta\vec{l}$ . Dla każdego elementu obliczamy wartość iloczynu skalarnego $\vec{B}\cdot\Delta\vec{l}$ . Suma tych iloczynów dla wszystkich elementów zamkniętej drogi nazywa się cyrkulacją indukcji $\vec{B}$ i wyraża się następująco:

cyrkulacja\:=\underset{po\, drodze\, zamkni\ogonek{e}tej}{\sum}\vec{B}\cdot\Delta\vec{l}

( 3.22 )

Pamiętamy, że $\vec{B}\cdot\Delta\vec{l}=B\Delta l\cos\alpha$ lub $\vec{B}\cdot\Delta\vec{l}=\Delta l\left(B\cos\alpha\right)=\Delta lB_{l}$ , więc $\vec{B}\cdot\Delta\vec{l}$ jest po prostu iloczynem $\Delta l$ i $B_{l}$ , gdzie $B_{l}$ oznacza rzut wektora $\vec{B}$ na kierunek $\Delta\vec{l}$ .

Ilustracja 3.26. **Sumowanie iloczynów $\vec{B}\cdot\Delta\vec{l}=B\Delta l\cos\alpha$ po drodze zamkniętej w polu magnetycznym**

a) droga sumowania i kołowe linie pola , b) droga sumowania i linie pola innego kształtu

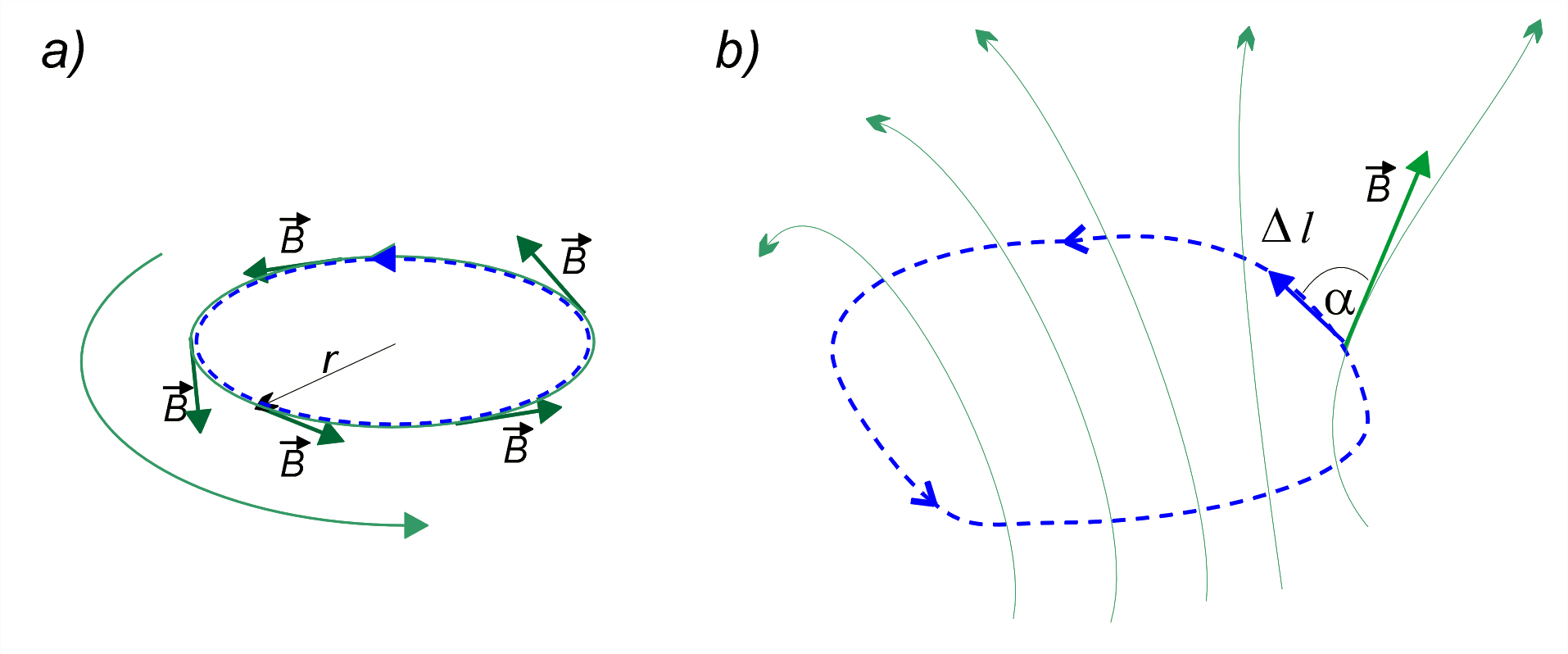
Widzimy więc, że lewa strona równości (3.21) to cyrkulacja po okręgu wektora indukcji pola magnetycznego wytworzonego przez prostoliniowy przewodnik z prądem (patrz il. 3.26a). Prawa strona tej równości z kolei mówi nam, że cyrkulacja jest równa natężeniu prądu mnożonemu przez $\mu_{0}$ .

Równanie (3.21) to nic innego jak prawo Ampère'a zastosowane do szczególnego przypadku – pola magnetycznego wytworzonego przez długi prostoliniowy przewodnik z prądem. W przypadku dowolnego pola magnetycznego, dla dowolnego układu prądów i dla dowolnej drogi obliczania cyrkulacji (czyli sumowania elementów $\vec{B}\cdot\Delta\vec{l}$ ), prawo Ampère'a formułujemy następująco:

Cyrkulacja wektora indukcji magnetycznej po dowolnej krzywej zamkniętej jest równa algebraicznej sumie natężeń prądów $I$ przepływających przez dowolną powierzchnię rozpiętą na tej krzywej, pomnożonej przez przenikalność magnetyczną próżni $\mu_{0}$ :

\underset{po\, drodze\, zamkni\ogonek{e}tej}{\sum}\vec{B}\cdot\Delta\vec{l}=\mu_{0}I

( 3.23 )

Przenikalności magnetycznej próżni $\mu_{0}$ przypisujemy wartość:

\mu_{0}=4\pi\cdot10^{-7}\frac{T\cdot m}{A}

Przykład 4

Znając wartości i jednostki przenikalności elektrycznej próżni $\varepsilon_{0}=8,854\cdot10^{-12}\frac{C^{2}}{J\cdot m}$ i przenikalności magnetycznej próżni $\mu_{0}=4\pi\cdot10^{-7}\frac{T\cdot m}{A}$ , można łatwo wykazać, że odwrotność ich iloczynu ma wartość kwadratu prędkości światła w próżni:

\begin{array}{c} \frac{1}{\varepsilon_{0}\mu_{0}}=\frac{1}{8,854\cdot10^{-12}\frac{C^{2}}{J\cdot m}\cdot4\cdot3,14\cdot10^{-7}\frac{T\cdot m}{A}}=\\ =\frac{1}{11,1\cdot10^{-18}\frac{s^{2}}{m^{2}}}=9\cdot10^{16}\frac{m^{2}}{s^{2}}=\left(3\cdot10^{8}\frac{m}{s}\right)^{2}=c^{2} \end{array}

Zatem:

c^{2}=\frac{1}{\varepsilon_{0}\mu_{0}}

( 3.24 )

Wynik nasz nie jest tylko „liczbowym” zbiegiem okoliczności, lecz ma głębszy sens, gdyż jest wyrazem tego, co odkrył Maxwell w połowie XIX wieku: z praw elektromagnetyzmu wynika, że istnieją fale elektromagnetyczne. Wykazano również, że światło jest falą elektromagnetyczną. Naturalne jest więc, że prędkość propagacji tej fali związana jest z właściwościami elektrycznymi i magnetycznymi próżni (lub innego ośrodka, w którym ta fala się rozchodzi).

Przykład 5

Jaka siła działa na pojedynczy ładunek $q=-1\, mC$ (il. 3.27) poruszający się równolegle do prostoliniowego przewodnika z prądem, w odległości $r=2\, cm$ od niego? (Podobna sytuacja dla elektronu została przedstawiona w rozdziale 3.3. Siła Lorentza i wektor indukcji pola magnetycznego – il. 3.14). Przyjmij, że ładunek $q$ porusza się z prędkością równą prędkości unoszenia elektronów, które stanowią prąd w przewodniku, $v=u_{D}=10^{-4}\frac{m}{s}$ . Koncentracja swobodnych elektronów w przewodniku wynosi $n=2,3\cdot10^{28}\, m^{-3}$ , a jego przekrój $S=100\, mm^{2}$ .

Ilustracja 3.27. **Ładunek $q$ poruszający się wzdłuż przewodnika doznaje działania siły magnetycznej**

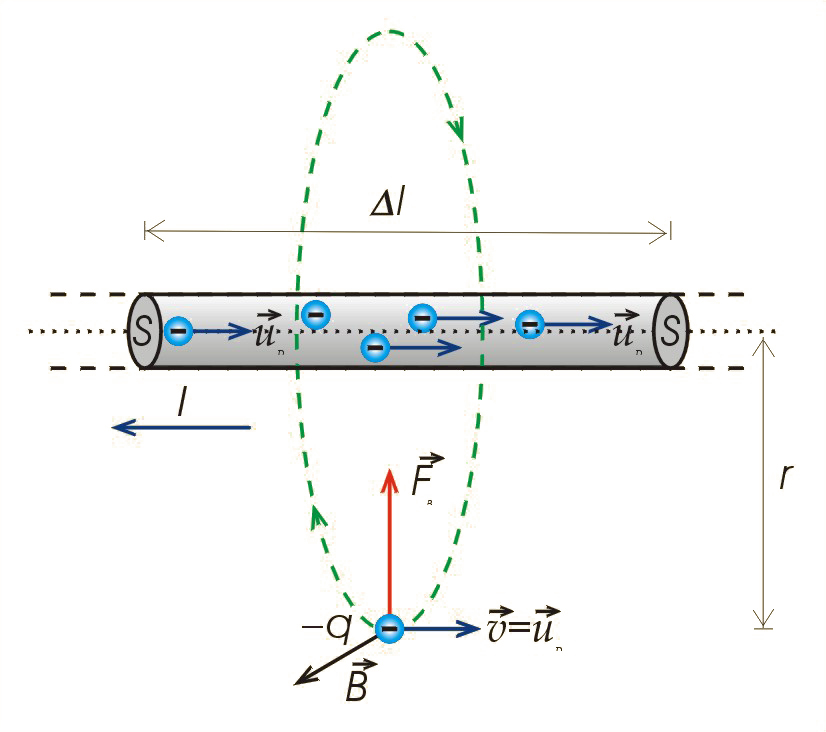
Rozwiązanie: Ładunek poruszający się wzdłuż przewodnika z prądem doznaje działania siły Lorentza $\vec{F_{B}}$ , która w tym przypadku jest zwrócona w stronę przewodnika. Zgodnie ze wzorem ogólnym (3.4), siła Lorentza działająca na ładunek punktowy poruszający się z prędkością $v$ wynosi $F_{B}=qvB$ . Zgodnie ze wzorem (3.20), indukcja $B$ wynosi $B=\frac{\mu_{0}I}{2\pi r}$ , zatem:

F_{B}=qvB=qv\frac{\mu_{0}I}{2\pi r}

( 3.25 )

Natężenie prądu w przewodniku wynosi:

I=\frac{\Delta q}{\Delta t}=\frac{\rho_{e}\Delta V}{\Delta t}=\frac{\rho_{e}\Delta l\, S}{\Delta t}=\rho_{e}u_{D}S=\rho_{e}vS

gdzie $\rho_{e}$ oznacza gęstość ładunku elektrycznego w elemencie objętości $\Delta V$ przewodnika o przekroju $S$ i długości elementu $\Delta l$ . Po podstawieniu tego wyniku do wzoru (3.25) otrzymamy:

F_{B}=\frac{\mu_{0}}{2\pi}\cdot\frac{qv^{2}\rho_{e}S}{r}

( 3.26 )

Po podstawieniu odpowiednich wartości i uwzględnieniu, że $\rho_{e}=en=1,6\cdot10^{-19}\cdot2,3\cdot10^{28}\frac{C}{m^{3}}$ , otrzymamy $F_{B}=3,68\cdot10^{-11}\, N=36,8\, pN$ .

Pytania i problemy

Wykaż, że jednostki przenikalności magnetycznej próżni można wyrazić jako: $\left[\mu_{0}\right]=\frac{1\, N}{1\, A^{2}}$ .
W elektrostatyce odpowiednik prawa Ampère'a głosi, że cyrkulacja pola elektrostatycznego obliczona dla dowolnej krzywej zamkniętej wynosi zero, bez względu na położenie ładunków, będących źródłem tego pola. Ogólny dowód tego prawa nie jest prosty.
Możesz jednak wykazać, że cyrkulacja pola elektrycznego wynosi zero w trzech szczególnych przypadkach:

a) Źródłem pola elektrycznego jest ładunek punktowy, a jako krzywą zamkniętą wybieramy okrąg o promieniu $R$ , w środku którego znajduje się ów ładunek.

b) Źródłem jednorodnego pola elektrycznego jest układ dwóch równomiernie naładowanych płaszczyzn (kondensator płaski), a jako krzywą zamkniętą wybieramy kwadrat o boku $a$ , mieszczący się między płaszczyznami.

c) Źródłem jednorodnego pola elektrycznego jest układ dwóch równomiernie naładowanych płaszczyzn (kondensator płaski), a jako krzywą zamkniętą wybieramy okrąg o promieniu $R$ , mieszczący się między płaszczyznami.