8.D1. Dodatek: Holografia (temat nadobowiązkowy)

Dzisiaj hologramy używane są bardzo często. Jednak przeciętny człowiek często nie wie, w jaki sposób można utworzyć hologram i na czym ta technika polega. Teraz – po tym jak zapoznałeś się z dyfrakcją i interferencją światła – będziesz mógł zrozumieć, na czym polega holografia, którą w skrócie można określić jako szczególną metodę (dyfrakcyjną) tworzenia obrazów przestrzennych.

Zasadę holografii omówimy w kolejności takiej, jak w rzeczywistości idea ta się rodziła i dojrzewała – w trzech punktach:

teoria Abbego – dotyczy dwuetapowego procesu tworzenia się obrazów w soczewkach,
idea Wolfkego – odnosi się do rozdzielenia tych etapów,
metoda Gabora – dotyczy rejestracji i odtwarzania fazy fali ugiętej.

Teoria Abbego

Ernest Abbe, niemiecki fizyk drugiej połowy XIX wieku, był współzałożycielem zakładów optycznych Zeissa. Jego wspólnicy, znając talent Abbego, spodziewali się, że polepszy on jakość produkowanych przyrządów optycznych. Abbe nie tylko wpadł na szereg ciekawych pomysłów ulepszających produkowane przyrządy optyczne, ale opracował w roku 1873 teorię, która, jak się później okazało, stała się podstawą dzisiejszej holografii. Najłatwiej zrozumiemy podstawę teorii Abbego, gdy przeprowadzimy następujące doświadczenie:

Doświadczenie pokazowe

Przepuszczamy wiązkę światła lasera przez wąską szczelinę (ok. $0,2\, mm$ ). Za szczeliną ustawiamy soczewkę skupiającą w odległości trochę większej (o $\Delta f$ ) niż jej ogniskowa (np. $f=25\, cm$ ). Za soczewką ustawiamy ekran (białą kartkę kartonu) w takiej odległości od soczewki, aby jej ognisko znalazło się w płaszczyźnie ekranu (il. 8.65).

Ilustracja 8.65. **Doświadczenie ilustrujące teorię dwuetapowego procesu tworzenia się obrazu szczeliny za pomocą soczewki**

W płaszczyźnie ogniskowej zachodzi analiza przedmiotu (tutaj szczeliny) w postaci obrazu dyfrakcyjnego fali światła, zaś dalej następuje synteza i powstaje rzeczywisty obraz przedmiotu

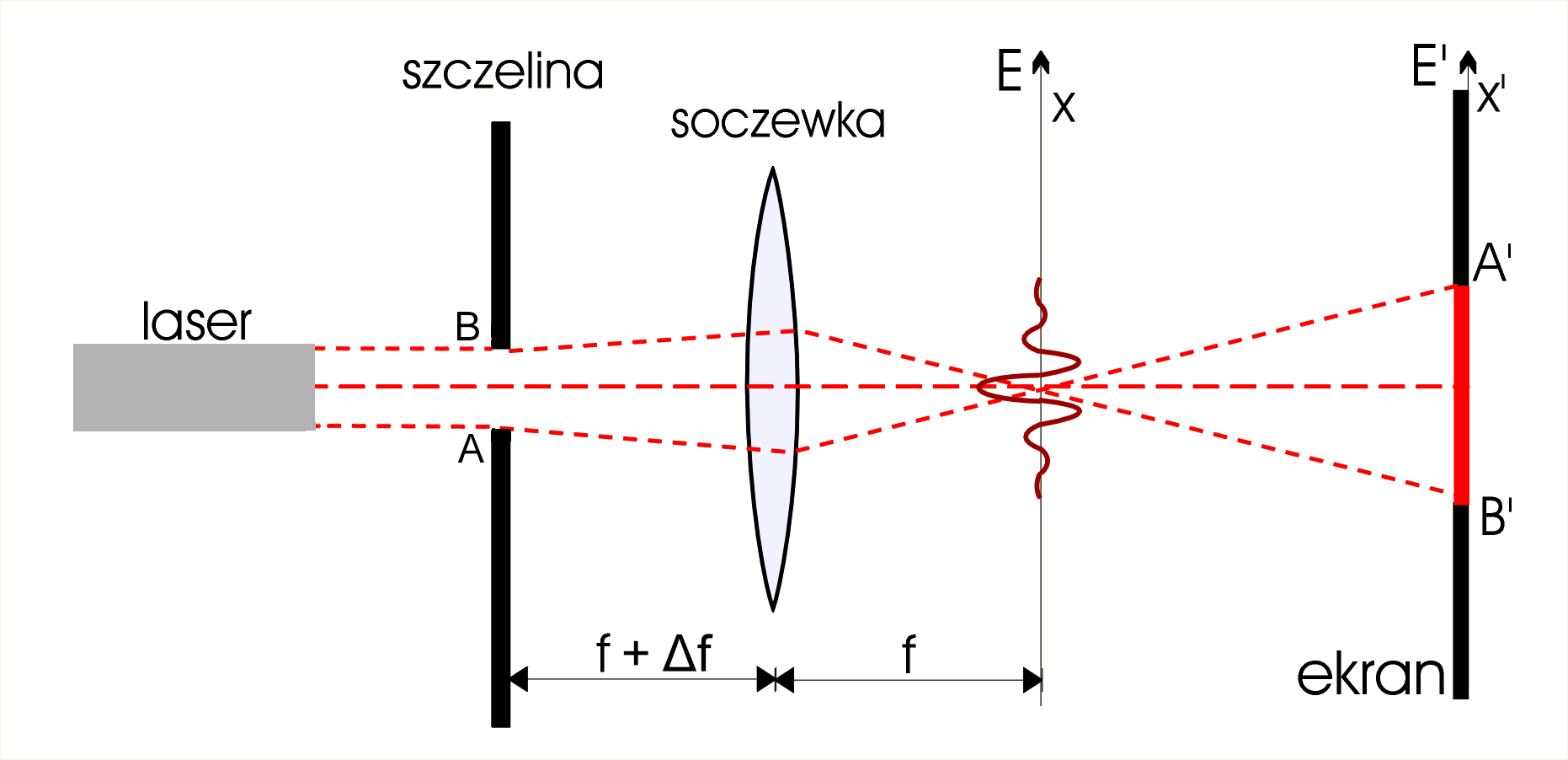
Na ekranie $E$ obserwujemy obraz dyfrakcyjny szczeliny w postaci prążków o zmniejszającej się jasności po obu stronach głównego prążka. Przesuwamy stopniowo ekran, obserwując w trakcie jego ruchu, jak początkowo prążki interferencyjne się rozmywają, a następnie skupiają się wszystkie razem, tworząc powiększony obraz rzeczywisty szczeliny, gdy ekran wejdzie w położenie $E'$ .

Wynik tego doświadczenia był właściwie łatwy do przewidzenia. Otrzymanie obrazu dyfrakcyjnego w płaszczyźnie ogniskowej soczewki jest naturalną konsekwencją dyfrakcji światła na pojedynczej szczelinie, co omówiono w rozdz. 8.6. Dyfrakcja i interferencja światła. Pierwsza część tego doświadczenia to właściwie powtórzone doświadczenie z tamtego rozdziału. Funkcja soczewki polega na skupianiu równoległych promieni w wiązkach ugiętego światła. Dostaliśmy zatem, dzięki soczewce, wyraźniejszy obraz dyfrakcyjny niż wtedy. Po przesunięciu ekranu w nowe położenie otrzymaliśmy ostry obraz szczeliny. Jest to zgodne z prawami optyki geometrycznej. Wiemy, że przecięcie promieni przechodzących przez soczewkę skupiającą daje obraz przedmiotu (tutaj szczeliny), który znajduje się przed soczewką.

Jednakże gdyby Abbe jedynie tak interpretował to doświadczenie, to niczego nowego by nie odkrył. Wprawdzie bez laserów (gdyż ich nie znano) wielu obserwowało podobne doświadczenia, ale jedynie Abbemu wpadła wspaniała myśl do głowy, dzięki której mógł stworzyć nową falową teorię tworzenia się obrazów za pomocą soczewek. Abbe zdawał sobie sprawę z tego, że prawa optyki geometrycznej są jedynie dość grubym przybliżeniem rzeczywistości. Postanowił stworzyć teorię opierającą się na własnościach falowych światła.

Abbe zrozumiał, że obraz tworzy się w dwóch następujących po sobie procesach. Pierwszy – to wytworzenie obrazu dyfrakcyjnego w płaszczyźnie ogniskowej – analiza dyfrakcyjna przedmiotu. Drugi proces – to synteza obrazu dyfrakcyjnego na ekranie. Można więc powiedzieć, że za płaszczyzną ogniskową następuje dyfrakcja dyfrakcji, czyli ponowne połączenie się światła w falę o kształcie podobnym do tego, jaki miała przy opuszczeniu przedmiotu (w naszym doświadczeniu – szczeliny).

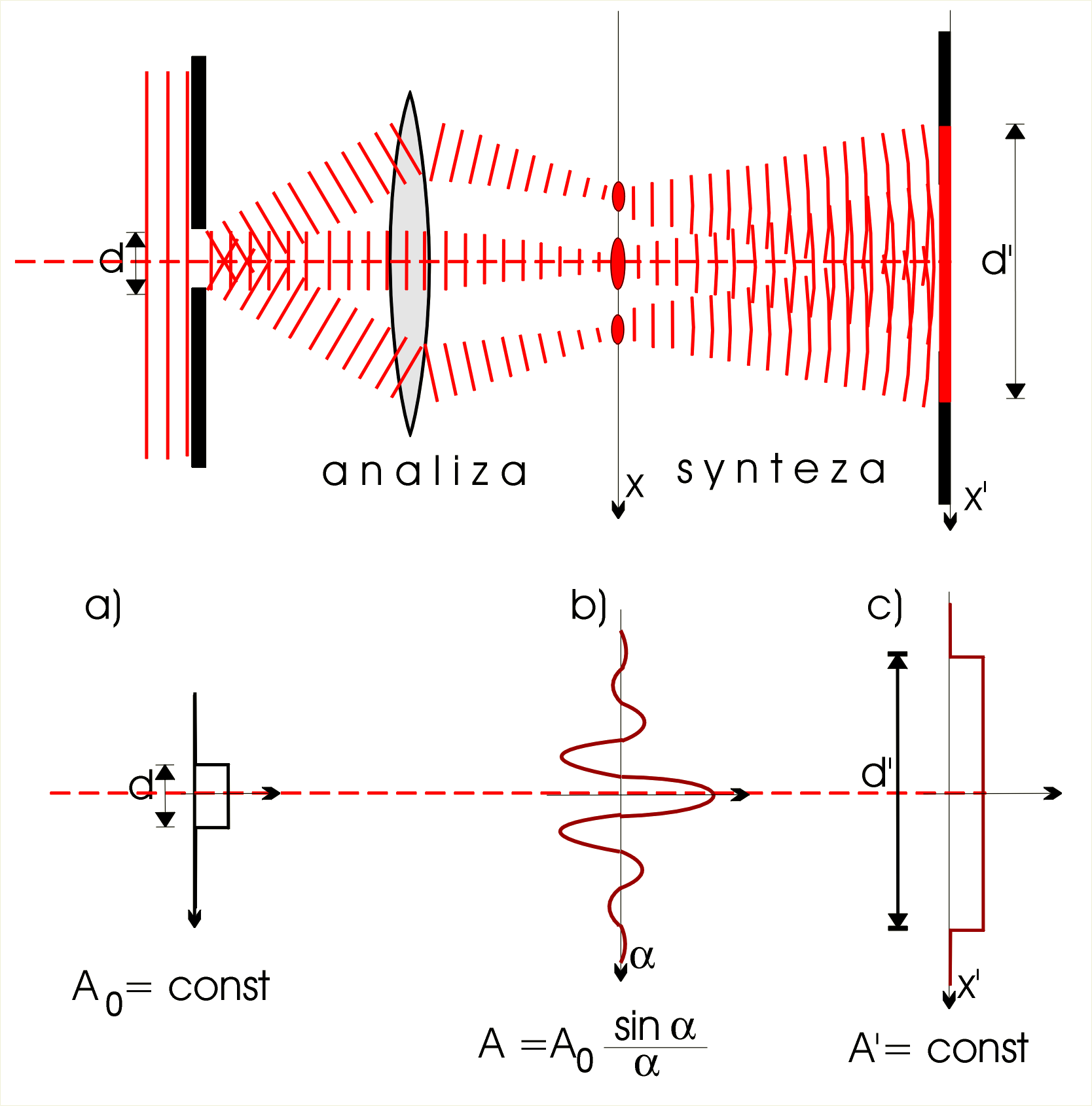
Zatem zgodnie z teorią Abbego doświadczenie to powinniśmy interpretować następująco: Fala o stałej amplitudzie $A_{0}$ przechodzi przez szczelinę (il. 8.66a) i ugina się zgodnie ze wzorem określającym amplitudę fali dyfrakcyjnej (8.24):

A_{w}=A_{0}\frac{\sin\alpha}{\alpha}

( 8.64 )

jak na il. 8.66b (zwróćmy uwagę na to, że wyrażenie (8.64) przyjmuje wartości dodatnie i ujemne; gdybyśmy ustawili ekran w płaszczyźnie ogniskowej, zaobserwowalibyśmy nie amplitudę fali, ale wielkość odpowiadającą natężeniu $I\sim A_{w}^{2}$ , które jest zawsze dodatnie). Następnie na ekranie powstaje ponownie fala o jednakowej amplitudzie $A'$ (il. 8.66c).

Idea Wolfkego rozdzielenia etapów tworzenia obrazu

Polski fizyk Mieczysław Wolfke – profesor Politechniki Warszawskiej – opracował w 1920 roku podstawy teoretyczne metody rozdzielenia w przestrzeni i w czasie etapów tworzenia obrazu przewidzianych w teorii Abbego – procesu analizy i syntezy. Zaproponował rejestrację obrazu dyfrakcyjnego na kliszy fotograficznej, a następnie odtworzenia procesu syntezy obrazu przez odpowiednie oświetlenie tej kliszy.

Można powiedzieć, że ta idea stała się podstawą holografii, z jednym jednak zastrzeżeniem. Mianowicie Wolfke zdawał sobie sprawę z tego, że jego metoda nie jest doskonała, gdyż zarejestrowany obraz dyfrakcyjny na kliszy niesie informację jedynie o natężeniu fali, nie zawiera natomiast informacji o fazie fali (przykładowo – w przypadku dyfrakcji na jednej szczelinie natężenie jest proporcjonalne do kwadratu amplitudy fali danej wzorem (8.25), która jest zawsze dodatnia. We wzorze tym zostaje zgubiona informacja o znaku „-” lub „+” tej amplitudy, co oznacza brak informacji o fazie fali ugiętej).

Mimo tego idea Wolfkego została zrealizowana i z powodzeniem zastosowana do badania struktury kryształów przez Bragga w roku 1940.

Ilustracja 8.66. **Dwuetapowy proces tworzenia się obrazu**

a) fala o stałej amplitudzie $A_{0}=const$ przechodzi przez szczelinę i ugina się, dając b) falę dyfrakcyjną o zmiennej amplitudzie, po czym c) następuje synteza fali dyfrakcyjnej w jedną falę, znowu o stałej amplitudzie $A'$

Metoda Gabora rejestracji i odtwarzania fazy fali dyfrakcyjnej

Idea Wolfkego wymagała udoskonalenia, którego dokonał węgierski fizyk Dennis Gabor w roku 1949. Gabor podał metodę rejestracji fazy na kliszy. Ze względu na to, że taka klisza niesie pełną informację o fali dyfrakcyjnej, nazwano ją hologramem, a metodę dwuetapowego tworzenia obrazu – holografią (gr. holographe oznacza zapis całkowity). Dlatego powszechnie uważa się Gabora za odkrywcę holografii.

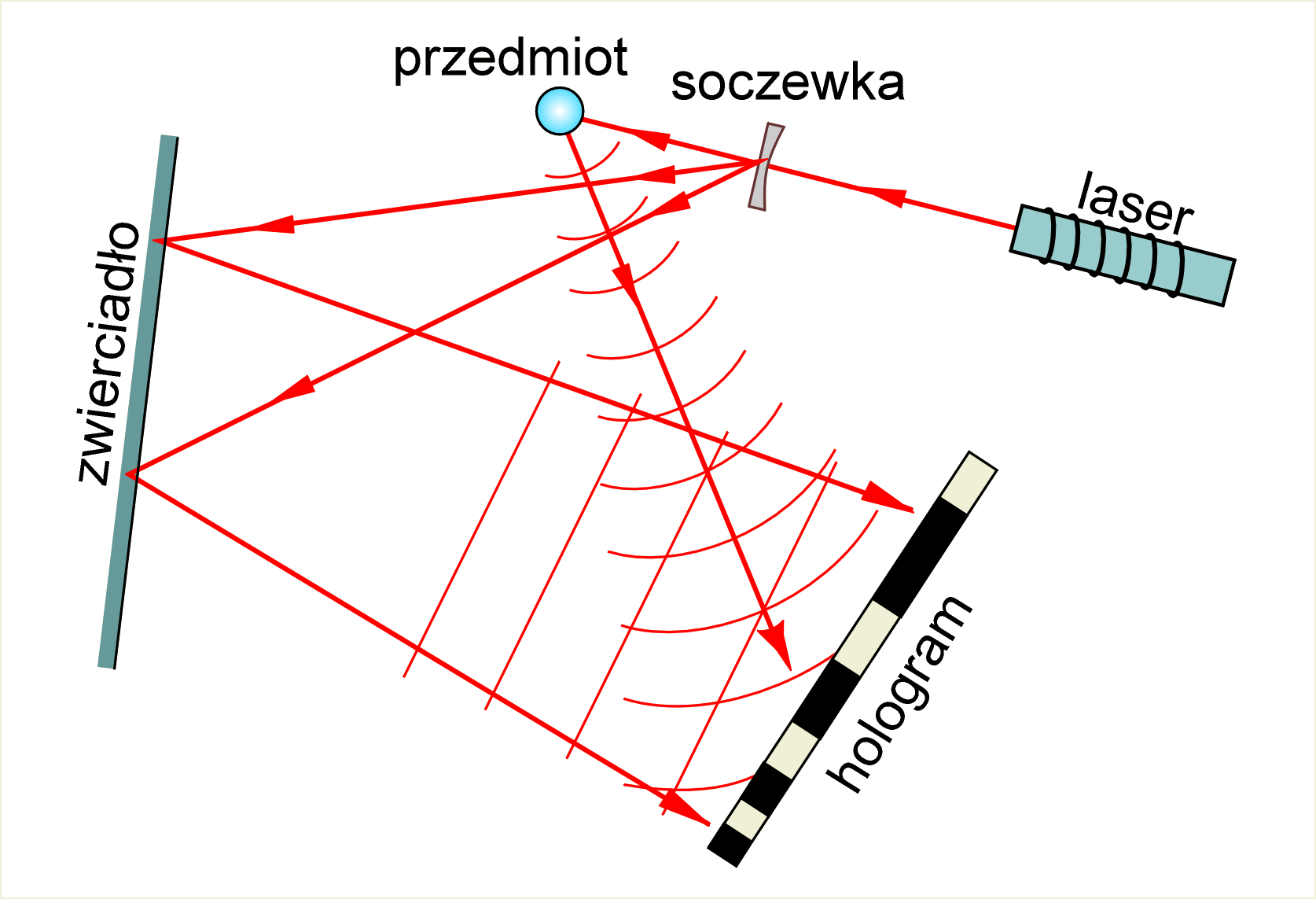
Zasada rejestracji fazy przedstawiona jest na il. 8.67. Na kliszę fotograficzną, na której ma być zarejestrowany obraz dyfrakcyjny przedmiotu (tutaj dla uproszczenia przyjęto przedmiot w postaci cienkiego pręcika, który jest prostopadły do płaszczyzny rysunku), pada jednocześnie wiązka ugięta od przedmiotu, jak również odbita od zwierciadła, tzw. fala odniesienia. Obie wiązki powstały z jednej wiązki światła z lasera rozdzielonej w soczewce. Gdyby nie było fali odniesienia, to klisza zarejestrowałaby tylko natężenie światła ugiętego. Fala odniesienia interferuje z falą ugiętą od przedmiotu, dając wzmocnienia fali wypadkowej, tam gdzie spotykają się w fazie zgodnej, a wygaszania, gdy spotkają się w przeciwnych fazach. W ten sposób stopień zaświetlenia kliszy jest zależny od natężenia fali ugiętej – od jej amplitudy, ale również od jej fazy.

Ilustracja 8.67. **Zasada rejestracji hologramu**

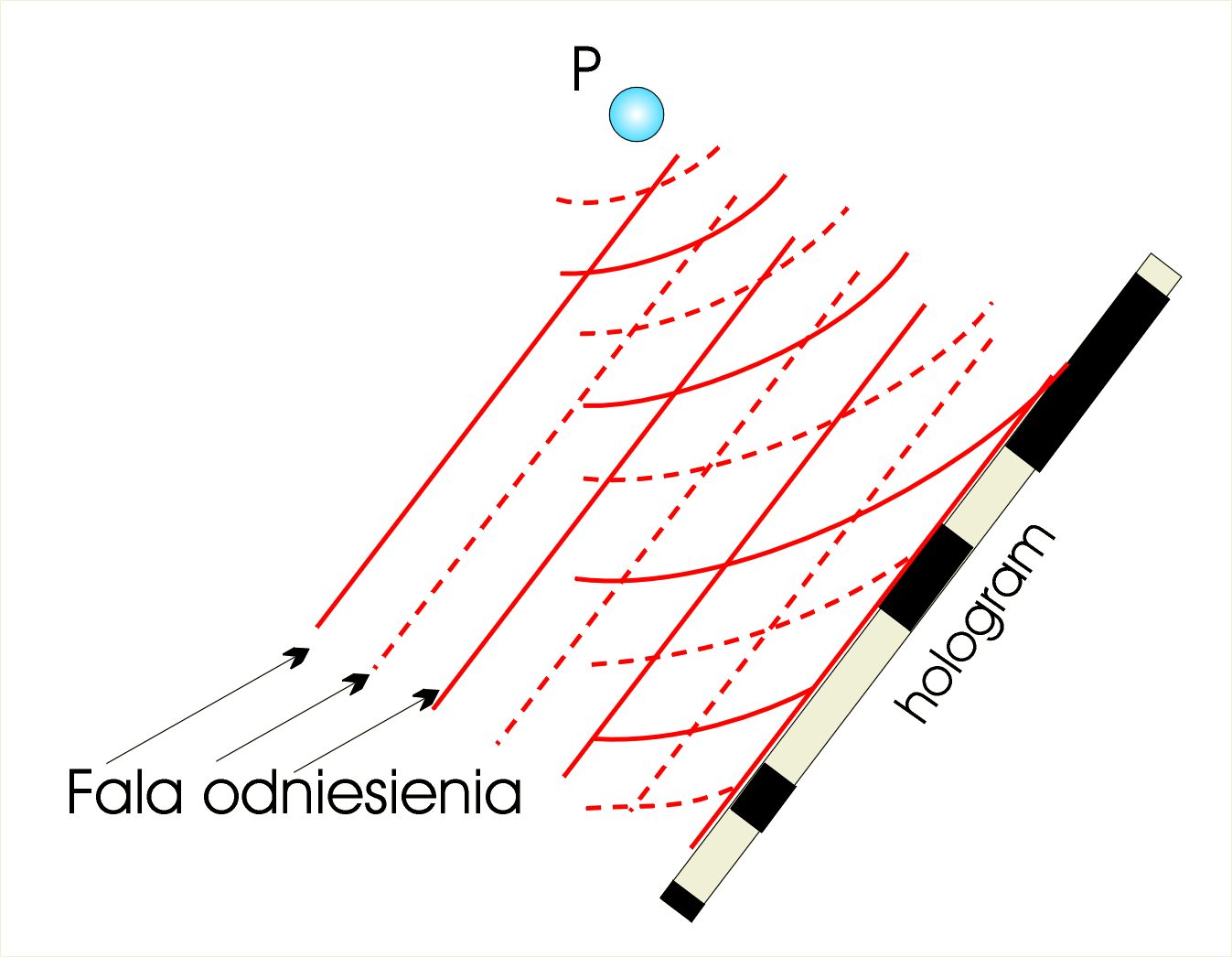
Sytuacja ta jest pokazana na il. 8.68, gdzie przedstawiono stan fal w jednej określonej chwili („zdjęcie migawkowe pola interferencyjnego fal”). Chwilowe położenia „grzbietów” fal zaznaczono liniami ciągłymi, a „dolin” – liniami przerywanymi. Tam gdzie spotyka się linia ciągła („grzbiet fali”) z linią przerywaną („doliną fali”) i gdzie występuje wzajemne wygaszenie fal – tam klisza się nie naświetla. Na odwrót – w miejscach, gdzie spotyka się linia ciągła z linią ciągłą (i przerywana z przerywaną), występuje wzmocnienie fal, a więc klisza naświetla się najsilniej. Jak widać, na kliszy-hologramie powstanie obraz dyfrakcyjny w postaci prążków. W przypadku takim jak na il. 8.68 prążki są rozmieszczone nierównomiernie, z malejącą odległością między nimi.

Ilustracja 8.68. **Powstawanie hologramu przedmiotu $P$**

Tak naświetlona klisza po wywołaniu staje się siatką dyfrakcyjną dla światła nań padającego (dla sytuacji przedstawionej na rysunkach jest to siatka dyfrakcyjna z malejącymi odległościami między szczelinami siatki). Przepuszczone przez nią światło lasera (il. 8.69) ulegnie ugięciu i odtworzy sytuację, która miała miejsce przy jej naświetlaniu w trakcie rejestracji hologramu.

Ilustracja 8.69. **Schemat odtwarzania powierzchni falowej w holografii**

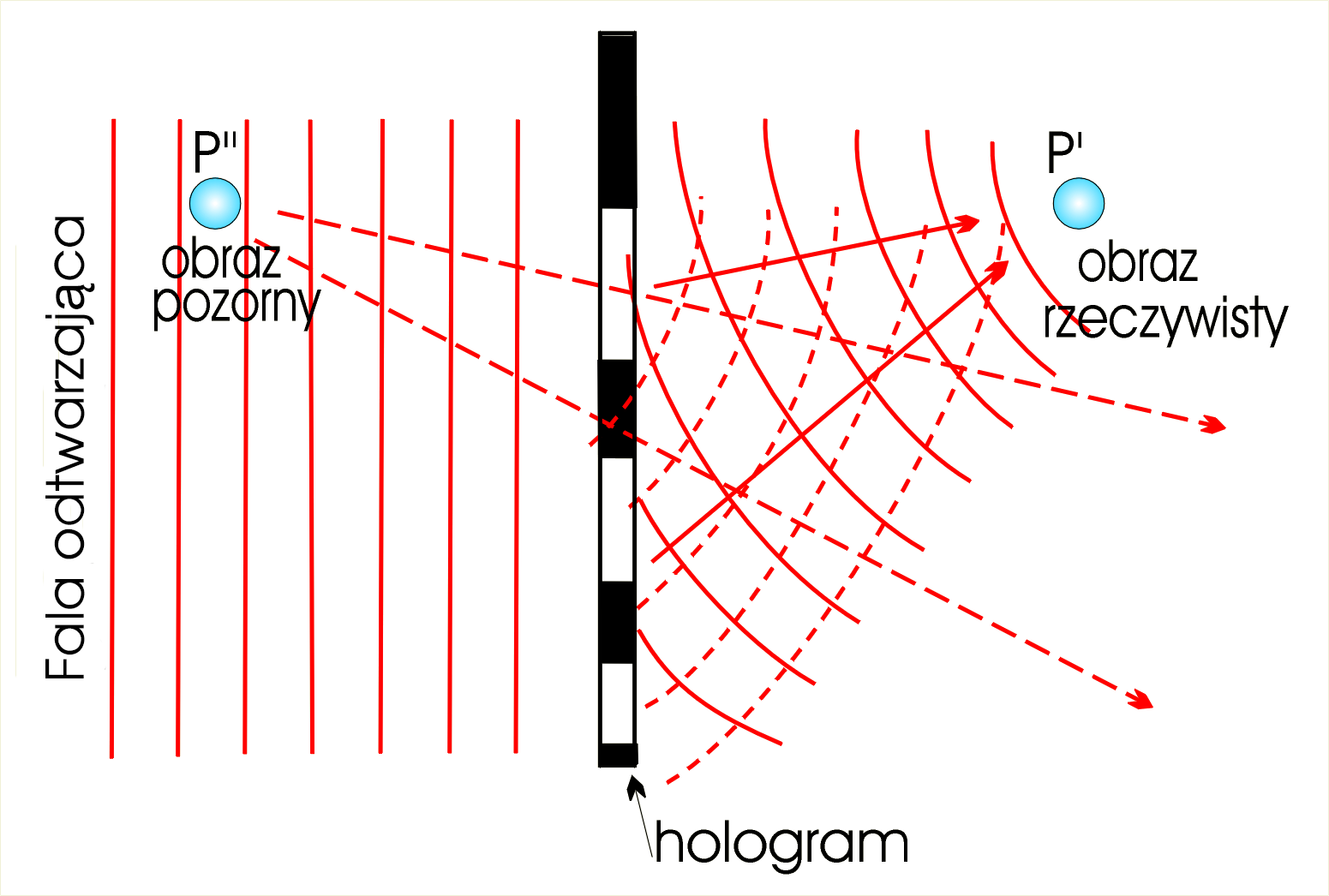
W ten sposób zostanie odtworzona fala, która była ugięta na przedmiocie $P$ , zbiegająca się właśnie do tego punktu (fala „wklęsła”, gdyż po przejściu fali płaskiej przez hologram – tutaj nierównomierną siatkę dyfrakcyjną – powierzchnia falowa się zagnie). Powstanie w ten sposób obraz rzeczywisty. Utworzy się również druga fala ugięta („wypukła”), rozbieżna, której przedłużenia promieni rozchodzą się z jednego miejsca – obrazu pozornego. Zatem hologram przy odtwarzaniu daje dwa obrazy przestrzenne – rzeczywisty i pozorny.

a) Tworzenie się hologramu w postaci regularnej siatki dyfrakcyjnej, gdy na kliszę padają dwie fale płaskie, b) odtwarzanie powierzchni falowej jest jednoznaczne ze zwykłą dyfrakcją na siatce dyfrakcyjnej — Ilustracja 8.70. a) tworzenie się hologramu w postaci regularnej siatki dyfrakcyjnej, gdy na kliszę padają dwie fale płaskie, b) odtwarzanie powierzchni falowej jest jednoznaczne ze zwykłą dyfrakcją na siatce dyfrakcyjnej

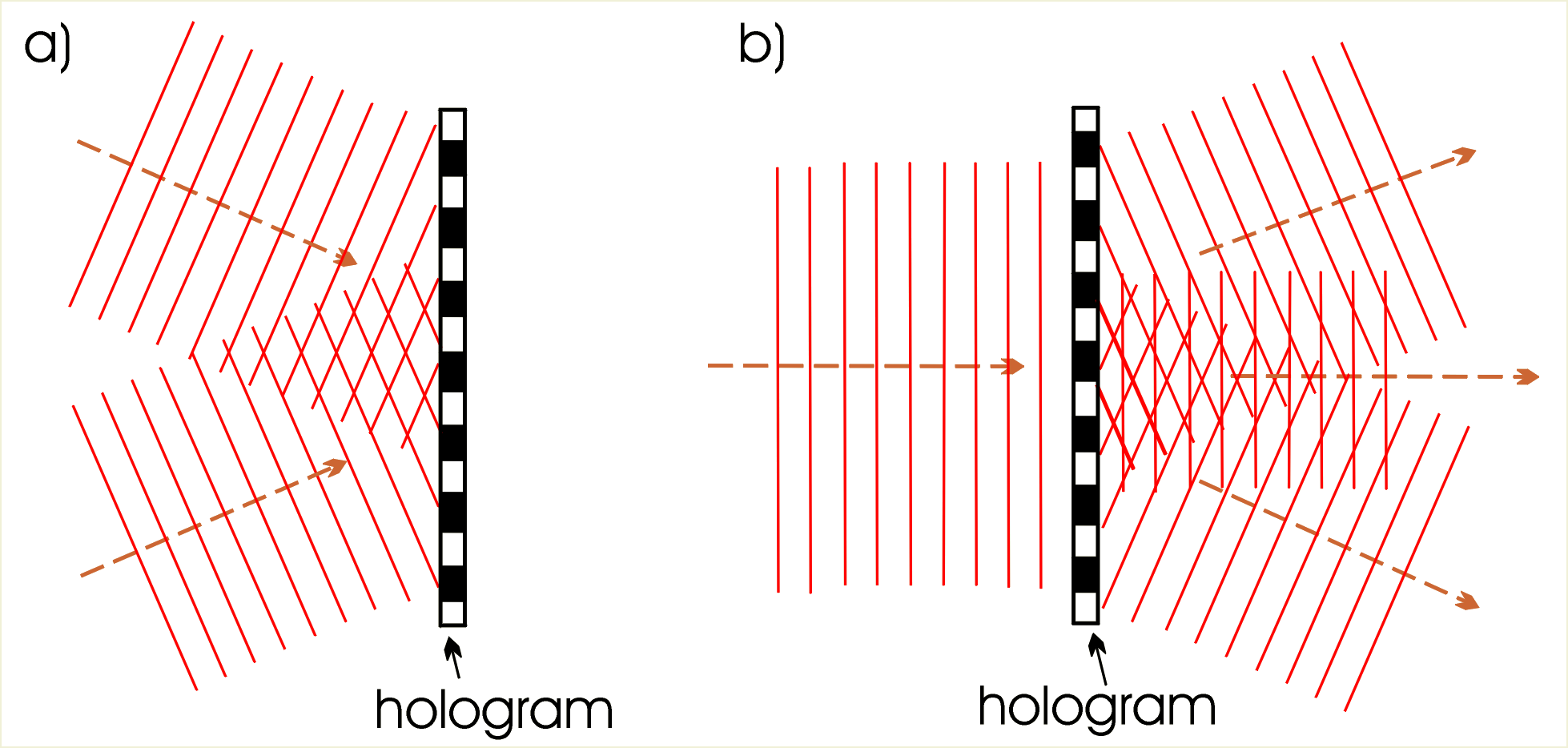
Dla porównania pokazano na il. 8.70a tworzenie się hologramu w postaci regularnej siatki dyfrakcyjnej, gdy fala ugięta od przedmiotu i fala odniesienia są płaskie. Odtwarzanie obrazu przy oświetleniu takiego hologramu niczym się nie różni od dyfrakcji fali na zwykłej siatce dyfrakcyjnej.

Jak widać, do uzyskiwania obrazów holograficznych nie są wymagane soczewki, gdyż obraz dyfrakcyjny przedmiotów powstaje również bez soczewek. Obecnie, gdy poprawiła się jakość wytwarzania hologramów, nie jest konieczne stosowanie laserów do odtwarzania obrazów holograficznych. Obrazy holograficzne są przestrzenne, a nie płaskie, jak w zwykłej fotografii czy w telewizji. Ze względu na swoje własności holografia znajduje wiele interesujących zastosowań i – jak się wydaje – może w przyszłości wyprzeć tradycyjną technikę telewizualną. Już dziś służy do znakowania towarów, wykrywania mikrodefektów w wyrobach technicznych, w medycynie – do wykrywania komórek rakowych we wczesnym stadium rozwoju. Może służyć do szyfrowania informacji oraz – w przyszłości – do holograficznego modelowania funkcji logicznych i pamięci optycznej w nowych generacjach komputerów.

Warto zwrócić uwagę, że holografia może wykorzystywać nie tylko fale świetlne, ale także np. akustyczne (tzw. holografia akustyczna).

Przykład 6

Hologram małej kulki powstał na skutek interferencji fali kulistej ugiętej na tej kulce z falą odniesienia płaską (il. 8.71). Odległość kulki od kliszy fotograficznej hologramu wynosi $x_{0}=0,5\, m$ . Długość fali światła wynosi $\lambda=640\, nm$ . Jak wygląda hologram?

Ilustracja 8.71. **Rejestracja hologramu małej kulki**

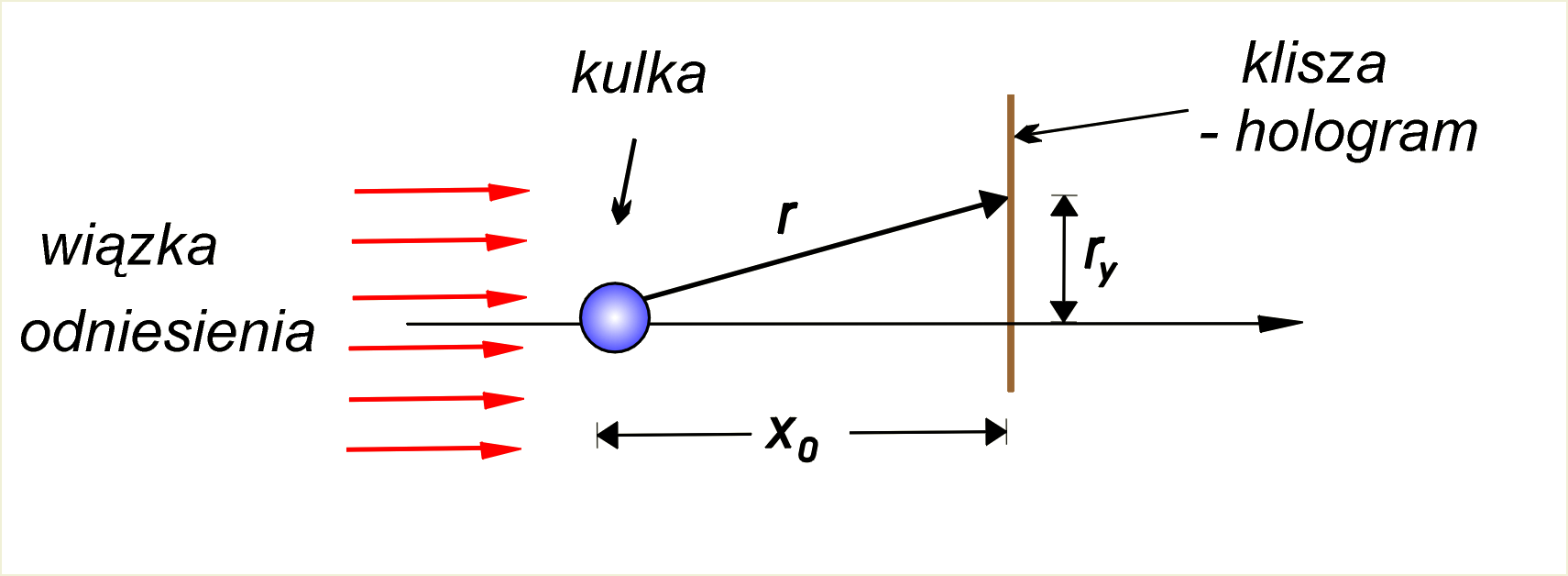
Rozwiązanie: Przyjmiemy zgodnie z ogólną postacią równania fali harmonicznej (5.4), że wartość wektora $E$ kulistej fali ugiętej wyraża się wzorem:

E=E_{u}\sin\left(\omega t-kr\right

Dla uproszczenia przyjęto, że amplituda fali $E_{u}$ jest stała w miejscach, gdzie fala osiąga kliszę. Natomiast fala odniesienia płaska będzie miała postać:

E=E_{0}\sin\left(\omega t-kx\right)

Na kliszy spotykają się obie fale i wzmacniają się w miejscach, gdzie różnica faz wynosi wielokrotność $2\pi$ , czyli:

$(\omega t-kx_{0})-(\omega t-kr)=kr-kx_{0}=2\pi m$ gdzie $m=1,\,2,\,3,\,...$

Skoro $k=2\pi/\lambda$ , to:

$r-x_{0}=m\lambda$ lub $r=m\lambda+x_{0}$

Wzmocnienia fali na płaskiej kliszy będą występować na koncentrycznych okręgach o promieniach $r_{y}$ . Na il. 8.71 widzimy, że $r=\sqrt{r_{y}^{2}+x_{0}^{2}}$ . Zatem:

\sqrt{r_{y}^{2}+x_{0}^{2}}=m\lambda+x_{0}

Stąd możemy obliczyć promienie okręgów, na których występują wzmocnienia fali:

r_{y}=\sqrt{2m\lambda x_{0}+m^{2}\lambda^{2}}\approx0,08\sqrt{m}\, cm

(W obliczeniu pominięto pod pierwiastkiem czynnik $m^{2}\lambda^{2}$ , gdyż $\lambda\ll x_{0}$ .)

Zatem hologram ma postać prążków w kształcie koncentrycznych okręgów. Pierwszy okrąg ma promień $0,8\, mm$ , drugi $1,13\, mm$ , trzeci $1,39\, mm$ itd.

Holografia komputerowa

Obecnie znaczny postęp w dziedzinie holografii dokonał się dzięki komputerom. W klasycznej holografii optycznej hologram powstaje w wyniku rejestracji pola interferencyjnego w realnym układzie optycznym. Natomiast komputer może wytworzyć hologram wirtualnie, zgodnie z naszą wiedzą teoretyczną. Dzięki temu otrzymuje się hologramy składające się z wygenerowanego wirtualnie układu prążków struktury dyfrakcyjnej. Taki hologram – wytworzony komputerowo – zastępuje prążki interferencyjne hologramu optycznego. Jednakże hologram komputerowy ma przewagę nad hologramem optycznym, gdyż generuje dużo mniejsze szumy (koherentne) niż hologram optyczny. Ponadto wydajność dyfrakcyjna tej metody jest większa. To znaczy, że za jej pomocą można wytwarzać hologramy bardziej złożone, niż pozwala na to technika optyczna.

Należy podkreślić, że to, co było niemożliwe w tradycyjnej holografii optycznej, stało się możliwe w holografii komputerowej. Przykładem może być holografia filmowa i telewizyjna.

Ilustracja 8.72. **Zdjęcie z pracowni holograficznej Wydziału Fizyki Politechniki Warszawskiej, która ma znaczny udział w rozwoju tej dziedzinie dziedziny wiedzy**

Pytania i problemy

Co to jest holografia? Na czym polega teoria Abbego dwustopniowego powstawania obrazu w soczewce? Na czym polega analiza dyfrakcyjna obrazu i jego synteza?
Na czym polegała stworzona przez Wolfkego idea rozdzielenia etapów tworzenia obrazu? Dlaczego za odkrywcę holografii uznaje się Gabora, a nie Wolfkego?
Na przykładzie przejścia światła przez pojedynczą szczelinę wyjaśnij zasadę teorii Abbego dwustopniowego powstawania obrazu w soczewce. Wykonaj odpowiednie rysunki.
Narysuj schemat układu dla rejestracji i odtwarzania hologramu. Na czym polega wynalazek Gabora rejestracji fazy obrazu dyfrakcyjnego?