Konstruowanie obrazu w soczewkach omawialiście już w gimnazjum. Teraz przypomnimy sobie te zagadnienia oraz wyprowadzimy wzór wiążący odległość przedmiotu i obrazu z ogniskową soczewki, tzw. wzór soczewkowy.

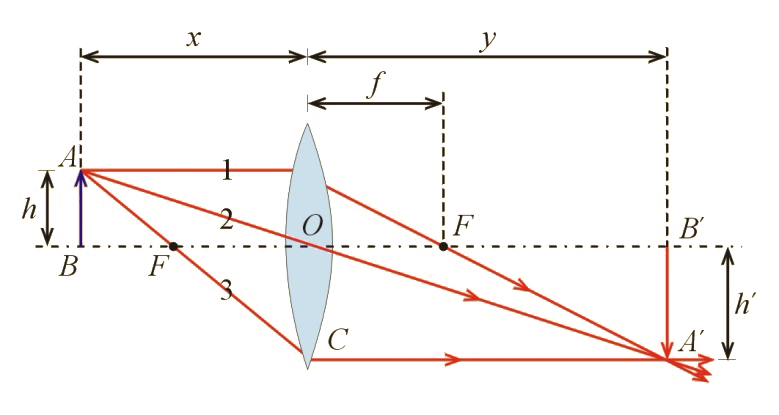
Weźmy pod uwagę soczewkę skupiającą. Konstruowanie obrazu opiera się na znajomości biegu promieni. Wystarczy znać bieg dwóch promieni, aby w miejscu ich przecięcia odwzorować obraz $A\text{'}$ punktu $A$, z którego te promienie wychodzą. Założymy, że punkt $A$ znajduje się w odległości większej niż ogniskowa, ale mniejszej niż podwójna ogniskowa, tzn. $f<x<2f$. Znamy przebieg przynajmniej trzech różnych promieni (il. 8.52):

1. promień równoległy do osi optycznej po przejściu przez soczewkę przejdzie przez ognisko $F$ położone po drugiej stronie soczewki,
2. kierunek promienia przechodzącego przez środek soczewki nie ulegnie zmianie,
3. promień przechodzący przez ognisko $F$ przed soczewką po przejściu przez soczewkę pobiegnie równolegle do osi optycznej soczewki. Bieg tego promienia jest analogiczny do biegu promienia $1$.

Na il. 8.52 widzimy, że otrzymamy w tym przypadku obraz rzeczywisty (rzeczywisty – to znaczy, że promienie odtworzą w rzeczywistości przedmiot w postaci obrazu utworzonego z punktów przecięcia się promieni) powiększony i odwrócony. Jeżeli punkt $A$ znajduje się w odległości większej niż podwójna ogniskowa, tzn. $x>2f$, to otrzymamy obraz rzeczywisty odwrócony i pomniejszony. Mamy tu sytuację odwrotną do poprzedniego przypadku (odwrotną w sensie zamiany miejscami przedmiotu i obrazu z odwróceniem zwrotu biegu promieni).

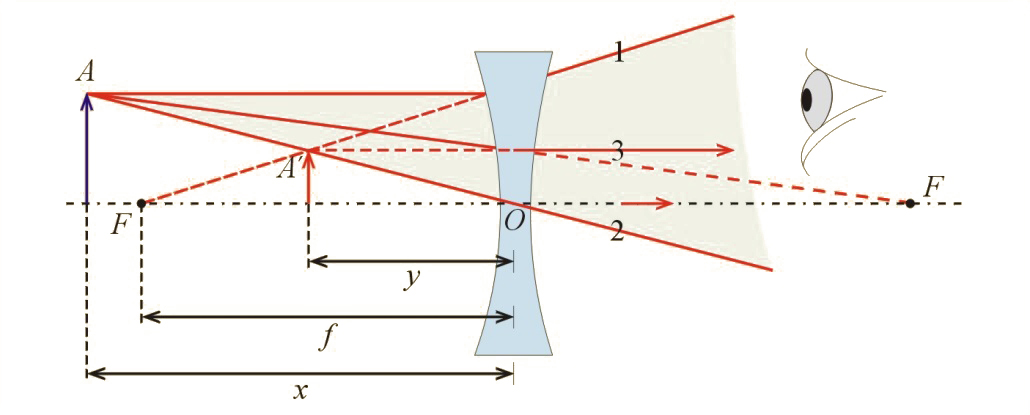
Jak powstaje obraz w soczewce rozpraszającej (jest to typowo soczewka wklęsła)? Zgodnie ze wzorem (8.45) zdolność skupiająca takiej soczewki jest ujemna (ponieważ promienie krzywizny powierzchni wklęsłych ograniczających soczewkę są ujemne) i ognisko soczewki jest urojone. Oznacza to, że promienie wiązki równoległej do osi optycznej soczewki po przejściu przez nią rozbiegają się w taki sposób, jak gdyby wychodziły z jednego punktu $F$ – z ogniska urojonego (il. 8.50b); ogniska takie występują po obu stronach soczewki w jednakowej od niej odległości. To nam pozwala ustalić, jaki będzie bieg promieni charakterystycznych przechodzących przez soczewkę rozpraszającą (il. 8.53):

1. promień równoległy do osi optycznej po przejściu przez soczewkę odchyli się od pierwotnego kierunku w ten sposób, że jego przedłużenie będzie przechodzić przez ognisko urojone $F$,
2. kierunek promienia przechodzącego przez środek soczewki nie ulegnie zmianie,
3. promień padający na soczewkę pod takim kątem do osi optycznej soczewki, że jego przedłużenie pada na ognisko urojone $F$ leżące po drugiej stronie soczewki, po przejściu przez soczewkę będzie biegł równolegle do osi optycznej soczewki.

Widzimy zatem, że w soczewce rozpraszającej rozbiegające się promienie nie mogą się przeciąć i dać obrazu podobnego do otrzymanego w przypadku soczewki skupiającej. A jednak za pomocą soczewki rozpraszającej można otrzymywać obrazy – obrazy urojone. Weźmy pod uwagę sytuację pokazaną na il. 8.53. Jeżeli oko umieścimy za soczewką, na drodze promieni rozbieżnych, to będzie nam się wydawać, że promienie te wychodzą z punktu $A\text{'}$ leżącego na przedłużeniu promieni wpadających do oka. Punkt ten jest obrazem pozornym (lub urojonym) punktu $A$.

Różnica między obrazem rzeczywistym a pozornym polega na tym, że obraz rzeczywisty powstaje przez rzeczywiste przecięcie się promieni i skupienie ich w miejscach, gdzie powstaje obraz (np. na ekranie lub białej ścianie). Następuje tam skupienie energii fali świetlnej, co może być ujawnione na przykład za pomocą kliszy fotograficznej lub fotokomórki. Obrazy pozorne natomiast mają znaczenie tylko subiektywne – to nam się wydaje, że promienie wychodzą jak gdyby z określonych punktów obrazu.

Bardzo prosto możemy teraz wyprowadzić tzw. wzór soczewkowy, który wiąże ze sobą odległość $x$ przedmiotu od soczewki, odległość $y$ obrazu od soczewki oraz ogniskową soczewki $f$. Wyprowadzimy go dla soczewki skupiającej, aczkolwiek będzie on również słuszny dla soczewki rozpraszającej. W tym celu napiszemy najpierw dwa równania – jedno wynika z podobieństwa trójkątów $ABO$ i $OB´A´$ (il. 8.52). Stosunek wielkości obrazu do wielkości przedmiotu, tzw. powiększenie, wynosi:

Drugie równanie wynika z podobieństwa trójkątów $OCF$ do $ABF$:

Po przyrównaniu prawych stron tych równań otrzymamy:

Stąd $xf=y\left(x–f\right)$ lub $xy=xf+yf$. Po podzieleniu tego równania przez $xyf$ otrzymamy ostatecznie wzór soczewkowy:

Jak już wspomnieliśmy, wzór ten, mimo że został wyprowadzony dla soczewki skupiającej, jest słuszny również dla soczewki rozpraszającej. Można go wyprowadzić podobnie. Spróbuj to zrobić, rozwiązując zadanie 3. z końca rozdziału. We wzorze soczewkowym odległość $x$ jest zawsze dodatnia, ogniskową $f$ dla soczewki rozpraszającej przyjmujemy jako ujemną, zaś dla soczewki skupiającej – jako dodatnią. Jeżeli otrzymamy dodatnią wartość $y$, to znaczy, że obraz jest rzeczywisty i powstaje po drugiej stronie soczewki, jeżeli natomiast $y$ jest ujemne, to obraz jest pozorny i powstaje po tej samej stronie soczewki co przedmiot.

Wzory (8.49) i (8.52) pozwalają przewidzieć, jaki będzie obraz przedmiotu – powiększony czy pomniejszony, rzeczywisty czy urojony – w zależności od odległości $x$ przedmiotu od soczewki.

Soczewka skupiająca:

1. dla $x<f$: $y<0$, $\left|p\right|>1$, obraz urojony powiększony,
2. dla $f<x<2f$: $y>2f$, $p>1$, obraz rzeczywisty powiększony,
3. dla $x>2f$: $f<y<2f$, $p<1$, obraz rzeczywisty pomniejszony.

Soczewka rozpraszająca:

1. Dla każdego $x$: $0>y>-f$, $\left|p\right|<1$, obraz urojony pomniejszony.

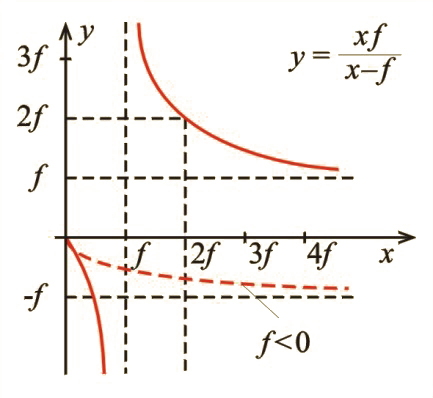
Wzór (8.52) można przekształcić w ten sposób, aby uzyskać zależność odległości $y$ od odległości $x$:

Wykres funkcji $y\left(x\right)$ przedstawiono na rysunku (il. 8.54), na którym linią ciągłą pokazano zależność dla soczewek skupiających $\text{(}f>0\text{)}$, zaś linią przerywaną zależność dla soczewek rozpraszających. Zwróć uwagę, że przy $f>0$ wykres ma asymptotę pionową dla $x=f$ – w tym punkcie wartość $y$ jest nieokreślona; obraz w ogóle nie powstaje.

EXE Obrazowanie za pomocą soczewki

Przykład 5

Jaką wartość powinna mieć ogniskowa soczewki skupiającej, pełniącej funkcję obiektywu rzutnika, który ma dawać ostry obraz przeźrocza o wysokości $h=\mathrm{2,5}\text{cm}$ na ekranie odległym od obiektywu o $y=4\text{m}$? Wysokość obrazu na ekranie ma wynosić $H=2\text{m}$.

Rozwiązanie: Powiększenie możemy obliczyć ze wzoru $p=\frac{H}{h}$. Znamy więc odległość $y$ i powiększenie $p$, a poszukujemy wartości ogniskowej $f$. W tym celu przekształcimy wzór soczewkowy (8.52) w następujący sposób:

$\frac{1}{f}=\frac{x+y}{xy}$, stąd $f=\frac{xy}{x+y}=\frac{y}{1+\frac{y}{x}}$.

Ponieważ $\frac{y}{x}=p=\frac{H}{h}$,

$$f=\frac{y}{1+p}=\frac{y}{1+\frac{H}{h}}=\frac{4\text{m}}{1+\frac{2}{\mathrm{0,025}}}=\mathrm{4,9}\text{cm}$$

Soczewka powinna mieć ogniskową równą 4,9 cm.

Pytania i problemy

1. Przedstaw na rysunku mechanizm powstawania obrazu w soczewce: a) skupiającej, b) rozpraszającej.
2. Wytłumacz, jaką zależność opisuje równanie nazywane wzorem soczewkowym. Wyprowadź to równanie.
3. Wzór soczewkowy (8.52) został wyprowadzony dla soczewki skupiającej. Jest on jednak słuszny również dla soczewki rozpraszającej. Wyprowadź w podobny sposób wzór soczewkowy dla takiej soczewki. Przyjmij, że zarówno $f$, jak i $y$ są formalnie ujemne.
4. Zdefiniuj powiększenie soczewki. Od czego ono zależy?