5.12. Fale stojące

Szczególnym przypadkiem interferencji dwóch fal jest fala stojąca. Można ją zademonstrować, w przypadku jednowymiarowego ośrodka, wykonując następujące doświadczenie.

Doświadczenie pokazowe

Aby wywołać falę, potrząsamy rytmicznie jednym końcem sznura przymocowanego drugim końcem do ściany, jak w doświadczeniu pokazowym. Fala odbija się od nieruchomego końca sznura i – nakładając się z falą biegnącą w przeciwną stronę – wytwarza w niektórych miejscach sznura szczególnie silnie drgania. W innych miejscach drgania praktycznie nie występują. Odkształcenia sznura nie przesuwają się wzdłuż sznura. Dlatego taką falę nazywamy falą stojącą, w przeciwieństwie do fali, w której drgania przemieszczają się z miejsca na miejsce.

Jak już wspomniano, w fali stojącej zarówno miejsca wychyleń maksymalnych, jak i miejsca, w których brak wychyleń, nie zmieniają swojego położenia. Miejsca wychyleń maksymalnych nazywamy strzałkami, miejsca, w których brak wychyleń, nazywamy węzłami.

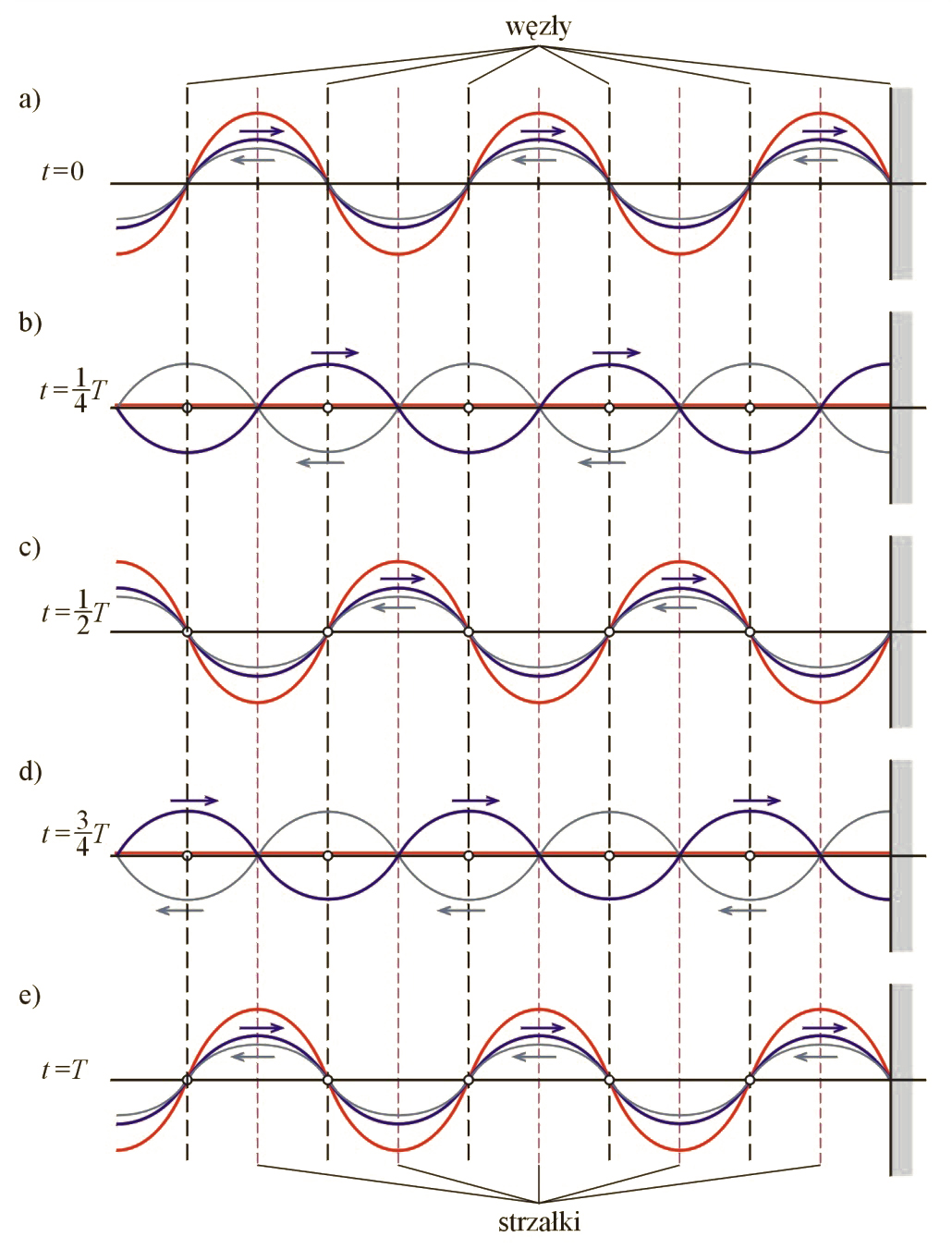
Rysunek (il. 5.32) wyjaśnia, dlaczego interferencja fali padającej z falą odbitą prowadzi do powstania fali stojącej. Przedstawiona została na nim sytuacja, gdy punkt odbicia jest sztywno zamocowany (odbicie od twardej ściany). Jest to istotne założenie, gdyż z teorii ruchu falowego wynika, że fala odbita od „ośrodka bardziej gęstego” zmienia fazę na przeciwną, co widać na il. 5.32.

Rysunek przedstawia jak gdyby „zdjęcia migawkowe” fali padającej, fali odbitej i fali wypadkowej w odstępach czasu co $\frac{1}{4}$ okresu. Dla ułatwienia interpretacji fala odbita ma na rysunku nieco mniejszą amplitudę niż padająca, choć na potrzeby wyznaczania fali wypadkowej przyjęto, że amplitudy obu fal są jednakowe.

Omówmy kolejne przypadki:

a) $t=0$ – widzimy, że cząstki w fali odbitej (która porusza się w lewo) są wychylone w tę samą stronę, co cząstki w fali padającej (poruszającej się w prawo), więc fala wypadkowa w tym momencie zostaje wzmocniona.

b) $t=\frac{T}{4}$ – fala odbita przesunęła się w lewo o ćwierć długości fali, a fala padająca – o tę samą wartość w prawo, więc obecnie cząstki w obu falach są wychylone przeciwnie; fale chwilowo wygaszają się wzajemnie.

c) $t=\frac{T}{2}$ – obie fale przesunęły się tak, że znowu się wzmacniają, ale faza fali wypadkowej jest przeciwna do fazy na rysunku a). I tak dalej.

Należy zauważyć, co widać wyraźnie na il. 5.32a-e, że najsilniejsze drgania fali wypadkowej (strzałki) występują zawsze w tych samych miejscach. Tak samo dotyczy punktów, w których brak wychyleń (węzły). Czyli strzałki i węzły są umiejscowione w fali wypadkowej, nie przesuwają się. Tak samo zresztą zachowują się miejsca drgań o mniejszych amplitudach. Dlatego taką falę wypadkową nazywamy falą stojącą. Łatwo możemy zauważyć, że odległość między dwoma sąsiednimi węzłami (jak i strzałkami) wynosi $\frac{\lambda}{2}$ , natomiast odległość węzła od najbliższej strzałki wynosi $\frac{\lambda}{4}$ .

Ilustracja 5.32. **Powstawanie fali stojącej jako wynik nakładania się fali padającej z falą odbitą**

Przykład 10: Fala stojąca w strunie

W strunie powstała fala stojąca, z dwiema strzałkami. Odległości między punktami wykonującymi drgania o jednakowej amplitudzie $A_{1}=4\, mm$ wynoszą $\Delta_{1}=3\, cm$ i $\Delta_{2}=7\, cm$ . Wyznacz długość fali oraz amplitudę $A_{0}$ w środku strzałki.

Rozwiązanie:

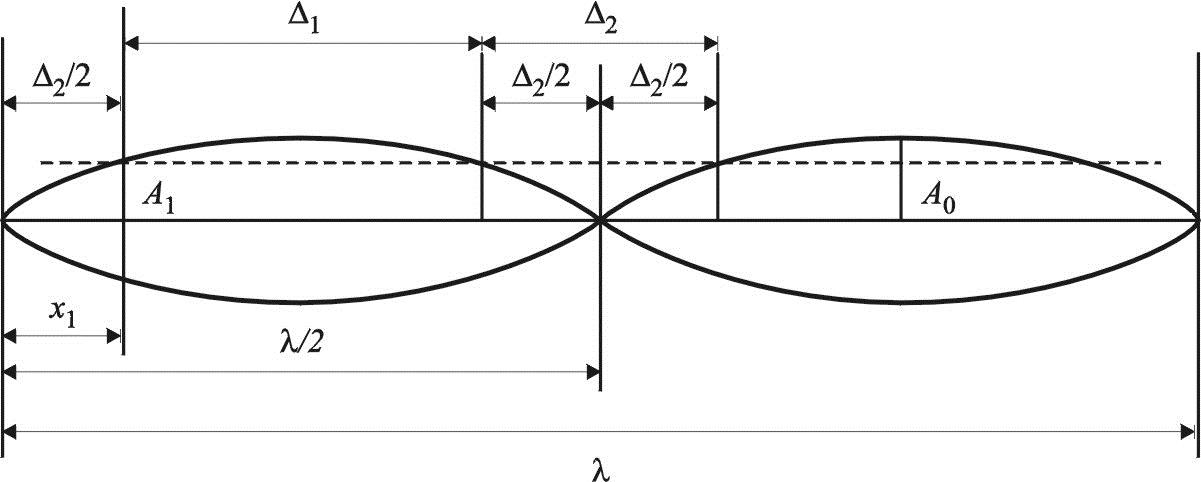
Ilustracja 5.33. **Fala stojąca – jedna długość fali**

1. Na długości $L$ odłożą się dwie połówki fali, czyli $L=\lambda$ .

2. Jednakową amplitudę fala osiąga w czterech miejscach, które można graficznie wyznaczyć, jeżeli poprowadzimy poziomą linię na wysokości $A_{1}$ . Odetnie ona falę stojącą w tych miejscach, w których ma ona jednakową amplitudę. Zaznaczamy te miejsca na osi $x$ .

3. Zauważmy, że miejsca o jednakowej amplitudzie są położone symetrycznie względem maksimów (strzałek fali) i minimum (węzła fali), tzn. znajdują się w jednakowej odległości $\Delta_{1}$ po obu stronach tych maksimów i muszą się znajdować też w jednakowej odległości $\frac{\Delta_{2}}{2}$ po obu stronach środkowego węzła.

Na podstawie rysunku można określić długość fali.

Aby znaleźć amplitudę w środku strzałki $A_{0}$ , należy napisać równanie fali stojącej. Stąd:

y=A_{0}\sin\frac{\pi}{L}x

( 5.53 )

odnoszące się do przypadku, gdy na odcinku $L$ odkładała się połówka fali. To równanie możemy zastosować wprost do połowy naszej struny, wykonując w nim odpowiednie podstawienie $L=\frac{\lambda}{2}$ . Mając to równanie, możemy podstawić współrzędną $x=x_{1}$ .

Na rysunku widać, że $\Delta_{1}+\Delta_{2}=\frac{\lambda}{2}$ . Zatem:

\lambda=2\left(\Delta_{1}+\Delta_{2}\right)=20\, cm

Aby znaleźć $A_{0}$ , napiszemy równanie amplitudy fali. W rozwiązaniu poprzedniego zadania otrzymaliśmy równanie amplitudy fali (5.53):

y=A_{0}\sin\frac{\pi}{L}x

odnoszące się do przypadku, gdy na odcinku $L$ odkładała się połówka fali. To równanie możemy zastosować wprost do połowy naszej struny, podstawiając $L=\frac{\lambda}{2}$ . Otrzymamy:

y=A_{0}\sin\frac{2\pi}{\lambda}x

( 5.54 )

Dla współrzędnej $x=x_{1}$ mamy:

A_{1}=y_{1}=A_{0}\sin\frac{2\pi}{\lambda}x_{1}

( 5.55 )

Na rysunku widać, że $x_{1}=\frac{\Delta_{2}}{2}$ , więc $A_{1}=A_{0}\sin\frac{\pi}{\lambda}\Delta_{2}$ . Stąd:

A_{0}=\frac{A_{1}}{\sin\frac{\pi}{\lambda}\Delta_{2}}=4,4\, mm

EXE Ćwiczenie wirtualne: Rura Kundta

Pytania i problemy

Wyjaśnij, na czym polega zjawisko powstawania fali stojącej. Co to są węzły i strzałki fali? Ile wynosi odległość między sąsiednimi strzałkami i sąsiednimi węzłami? Ile wynosi odległość między strzałką i sąsiadującym z nią węzłem?
W rozdziale 5.6. Podstawowe cechy fal rozważaliśmy falę stojącą w sznurze zamocowanym jednym końcem do ściany. Na tym końcu musiał powstać węzeł, gdyż tam sznur nie mógł drgać. Wtedy faza fali przy odbiciu ulegała zmianie o $\pi$ . Gdy sznur jest zawieszony na elastycznej nitce, jego koniec może wykonywać drgania i może tam powstać strzałka fali stojącej – faza fali przy odbiciu nie ulega zmianie. Wykonaj rysunek podobny do il. 5.32, aby odpowiedzieć na pytanie, jaki będzie wtedy rozkład węzłów i strzałek w fali stojącej.