8.11. Soczewka

Soczewka jest zwykle zbudowana ze szkła lub plastiku; jest to bryła ograniczona z dwóch stron powierzchniami kulistymi. Bywają też soczewki ograniczone powierzchniami walcowatymi czy parabolicznymi. Takich soczewek tutaj jednak rozpatrywać nie będziemy.

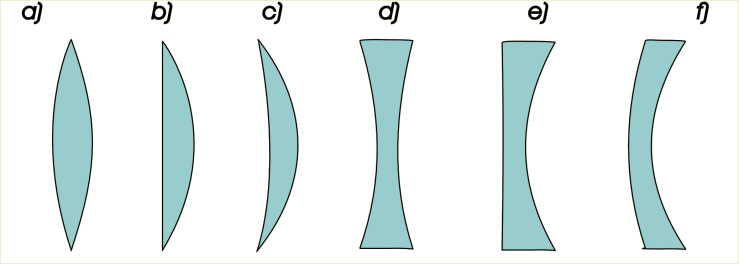
Możemy wyróżnić sześć postaci soczewek (il. 8.48): a) dwuwypukłe, b) płasko-wypukłe, c) wklęsło-wypukłe, d) dwuwklęsłe, e) płasko-wklęsłe, f) wypukło-wklęsłe. Prosta przechodząca przez środki powierzchni ograniczających soczewkę nazywa się główną osią optyczną soczewki. Soczewka wklęsło-wypukła różni się tym od soczewki wypukło-wklęsłej, że ta pierwsza jest najgrubsza w środku, a ta druga jest najcieńsza w środku. Soczewka wklęsło-wypukła należy do soczewek wypukłych („a”, „b” i „c” na il. 8.48), zaś soczewka wypukło-wklęsła do soczewek wklęsłych („d”, „e” i „f” na il. 8.48).

Weźmiemy pod uwagę cienką szklaną soczewkę dwuwypukłą. Pamiętamy na pewno jeszcze z gimnazjum, że jeżeli na taką soczewkę pada wiązka równoległa do osi optycznej, skupia się w jednym punkcie, zwanym ogniskiem, które zwykle oznacza się przez $F$ . Odległość ogniska od soczewki $f$ nazywa się ogniskową soczewki. Odwrotność ogniskowej soczewki $1/f$ (wyrażonej w metrach) nazywa się zdolnością skupiającą soczewki, oznaczamy ją symbolem $\Phi$ i wyrażamy w dioptriach $(D)$ (np. soczewka o ogniskowej równej $f=1\, m$ ma zdolność skupiającą $\Phi=1\, D$ , jeżeli $f=0,25\, m$ , to $\Phi=4\, D$ itd.).

Oto wzór na zdolność skupiającą soczewki:

\Phi=\frac{1}{f}=\left(n-1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right)

( 8.45 )

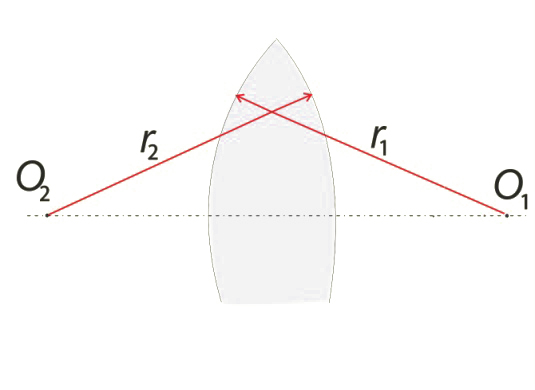
gdzie $r_{1}$ i $r_{2}$ – promienie sferycznych powierzchni soczewki (il. 8.49), $n$ – współczynnik załamania materiału soczewki.

Wzór (8.45) jest wzorem uniwersalnym i może służyć do obliczania zdolności skupiającej dowolnej soczewki cienkiej, jednakże należy pamiętać o znakach. W szczególności, gdy powierzchnia ograniczająca soczewkę jest wypukła, to jej promień jest dodatni, powierzchnia wklęsła ma – umownie – promień ujemny.

Ilustracja 8.50. Ogniskowanie wiązki paraksjalnej w soczewkach wykonanych z materiału o współczynniku załamania $n>1$ : a) wypukłej i b) wklęsłej

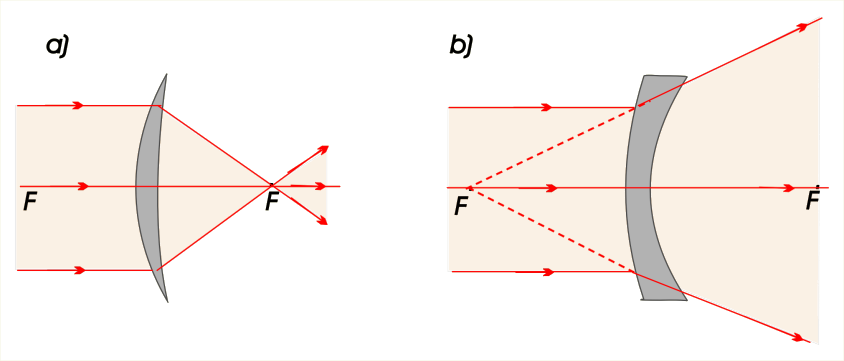
Płaszczyznę musimy traktować jako powierzchnię o nieskończenie dużym promieniu krzywizny. Uwzględniając te uwagi, łatwo możemy wykazać, że dla $n>1$ soczewki wypukłe mają zdolność skupiającą dodatnią, zaś soczewki wklęsłe – ujemną. Dlatego mówimy, że soczewki wklęsłe mają urojoną (ujemną) ogniskową. Na il. 8.50 przedstawiono ogniskowanie wiązki paraksjalnej (przyosiowej), czyli takiej, której szerokość jest dużo mniejsza od promienia krzywizny ograniczającej soczewkę (dotyczy soczewek wypukłych i wklęsłych wykonanych z materiału o współczynniku załamania $n>1$ ). Wzór (8.45) pozwala wyznaczyć zdolność skupiającą soczewki również dla $n \less 1$ ; wtedy otrzymujemy wynik odwrotny – soczewka wypukła jest rozpraszająca, a wklęsła – skupiająca.

Wyprowadzenie wzoru na zdolność skupiającą soczewki

Teraz wyprowadzimy wzór (8.45) na zdolność skupiającą soczewki, jeżeli dane są promienie sfer ograniczających soczewkę $r_{1}$ i $r_{2}$ oraz współczynnik załamania materiału soczewki. Przyjmiemy, że na cienką soczewkę pada wiązka światła równoległa do osi optycznej soczewki i że średnica wiązki światła jest mała w porównaniu z promieniami $r_{1}$ i $r_{2}$ (wiązka taka nazywa się paraksjalną).

Ilustracja 8.51. **Zależności kątowe przy przejściu promienia przez soczewkę, cienką soczewkę można w miejscu padania promienia traktować jako fragment pryzmatu**

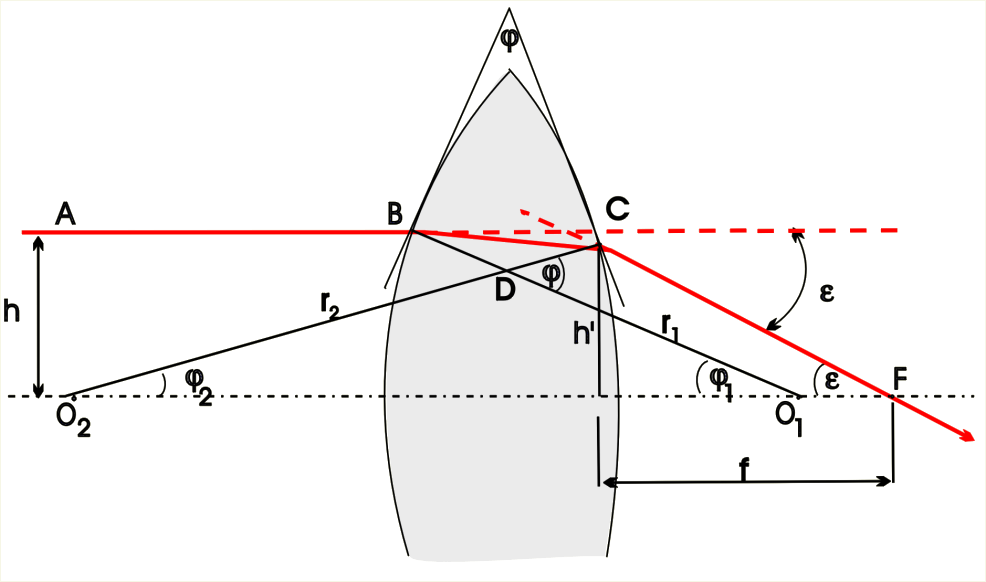
Na il. 8.49 przedstawiono promień $A B C F$ padający na soczewkę w punkcie $B$ i wychodzący z niej w punkcie $C$ . Te części powierzchni możemy uważać za płaskie, gdyż są małe w porównaniu z promieniami ich krzywizny. Płaszczyzny te przetną się pod pewnym kątem $\varphi$ (il. 8.49). Zatem przejście promienia przez soczewkę nie będzie się niczym różniło od przejścia przez pryzmat o kącie łamiącym $\varphi$ . Będzie więc słuszny przybliżony wzór, który wyprowadziliśmy dla pryzmatu:

\varepsilon=\left(n-1\right)\varphi

( 8.46 )

Na il. 8.49 widzimy, że kąt $\varphi$ jest również kątem zewnętrznym w trójkącie $O_{2}DO_{1}$ , więc $\varphi=\varphi_{1}+\varphi_{2}$ . Zatem:

\varepsilon=\left(n-1\right)\left(\varphi_{1}+\varphi_{2}\right)

( 8.47 )

We wzorze tym występują małe kąty, możemy więc zastąpić je sinusami lub tangensami. Wykonamy zatem następujące podstawienia:

$\varepsilon=\tan\varepsilon=\frac{h'}{f}$ , $\varphi_{1}=\sin\varphi_{1}=\frac{h}{f}\cong\frac{h'}{f}$ , $\varphi_{2}=\sin\varphi_{2}=\frac{h}{f}\cong\frac{h'}{f}$ .

Po wstawieniu tych wyrażeń do wzoru (8.47), i skróceniu przez $h'$ , ostatecznie otrzymamy:

\frac{1}{f}=\left(n-1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right)

( 8.48 )

Przykład 4

Mamy do dyspozycji szkło o współczynniku załamania $n=1,52$ i chcemy wykonać soczewkę wypukłą o zdolności skupiającej $\Phi=1/f=4\, D$ . Przyjmijmy, że soczewka ma być ograniczona powierzchniami sferycznymi o jednakowej krzywiźnie. Jaki powinien być promień krzywizny powierzchni soczewki?

Rozwiązanie: Skoro $r_{1}=r_{2}=r$ , to zgodnie z wzorem (8.45) $\Phi=\frac{1}{f}=\left(n-1\right)\frac{2}{r}$ , stąd $r=\frac{2\left(n-1\right)}{\Phi}$ .

Po podstawieniu wartości otrzymamy $r=0,26\, m=26\, cm$ . Widzimy, że promień krzywizny powierzchni tej soczewki jest tylko nieznacznie większy od ogniskowej, która wynosi $f=1/\Phi=1/4\, m=0,25\, m=25\, cm$ .

Pytania i problemy

Scharakteryzuj rodzaje soczewek ze względu na kształt ich powierzchni.
Czm są: ognisko, ogniskowa soczewki i zdolność skupiająca soczewki? W jakich jednostkach wyrażamy tę ostatnią?
Wytłumacz, jaką wiązkę światła nazywamy wiązką paraksjalną. Wyprowadź równanie opisujące zależność zdolności skupiającej soczewki od współczynnika załamania materiału soczewki i promieni krzywizn jej powierzchni.