8.1. Prawa odbicia i załamania światła

Na lekcjach w gimnazjum dowiedziałeś się, że podczas odbicia promienia światła obowiązuje prawo: kąt odbicia jest równy kątowi padania. Z kolei przy przechodzenia światła z jednego ośrodka do drugiego światło ulega załamaniu, a stosunek prędkości rozchodzenia się światła w tych ośrodkach jest równy współczynnikowi załamania $n$ . Teraz, znając podstawową zasadę ruchu fali, tj. zasadę Huygensa, będziesz mógł zrozumieć, dlaczego te prawa obowiązują.

Rozważymy płaską falę świetlną padającą na płaską gładką powierzchnię. Na il. 8.1 powierzchnię odbijającą falę oznaczono literami $M N$ . Czoło fali $A C$ jest prostopadłe do promieni fali $1$ i $2$ . Kąt padania $\alpha$ to kąt zawarty między promieniem a linią normalną, czyli prostą prostopadłą do płaszczyzny odbijającej $M N$ .

Czoło fali płaskiej odbitej — Ilustracja 8.1. Czoło $B D$ fali płaskiej odbitej jest utworzone przez nałożenie się elementarnych fal kulistych rozchodzących się od powierzchni odbijającej falę

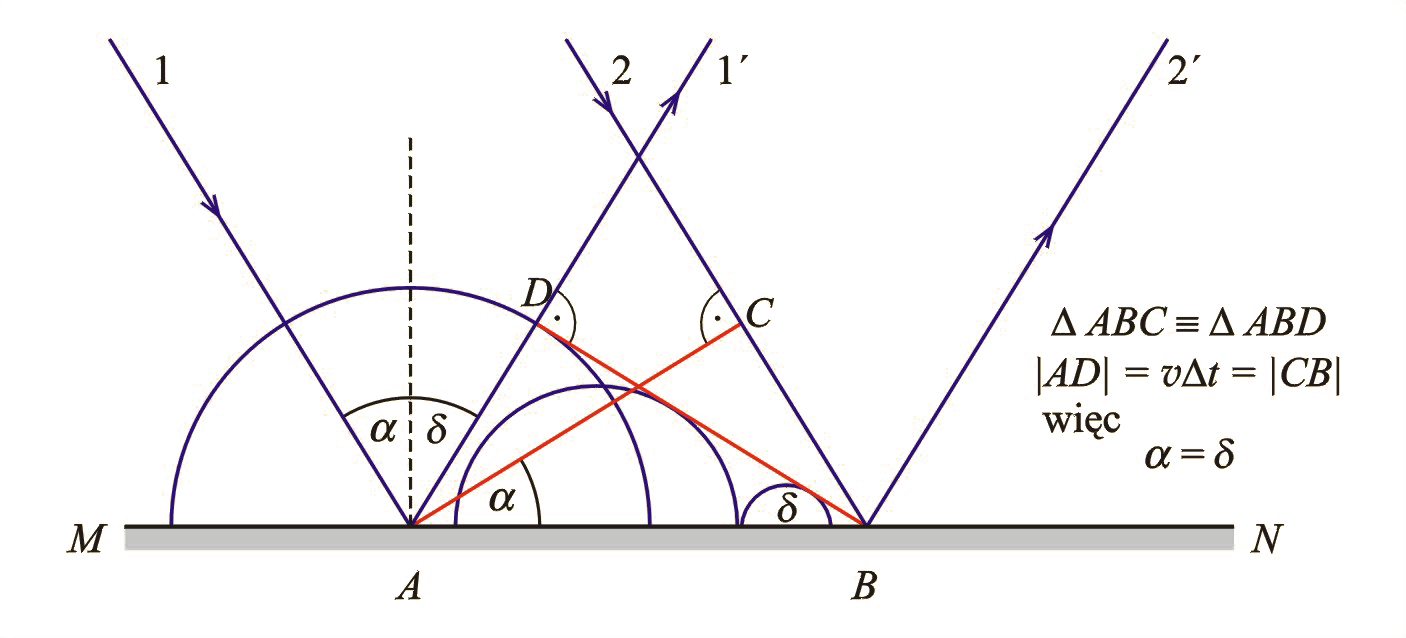
Zgodnie z zasadą Huygensa, mówiącą, że każdy punkt powierzchni falowej jest źródłem elementarnej fali wtórnej, powierzchnią falową fali odbitej będzie płaszczyzna styczna do elementarnych fal wtórnych, których środki leżą na płaszczyźnie $M N$ . Czoło fali padającej $A C$ nie dociera jednocześnie do tej płaszczyzny. Wzbudzenie drgań fali wtórnej w punkcie $A$ nastąpi o czas $\Delta t$ wcześniej niż w punkcie $B$ . W momencie, gdy fala dociera do punktu $B$ i zaczyna tam wzbudzać drgania, fala elementarna wzbudzona wcześniej w punkcie $A$ rozprzestrzeni się w postaci półsfery o promieniu równym $r=AD=v\Delta t$ . Półsfery fal elementarnych wychodzących z punktów położonych między punktami $A$ i $B$ będą miały promienie różnej długości, co zaznaczono na rysunku. Czoło fali odbitej $B D$ jest styczne do tych fal wtórnych i prostopadłe do promieni $1'$ i $2'$ wychodzących z punktów $A$ i $B$ .

Łatwo teraz możemy wykazać, że kąt odbicia $\delta$ jest równy kątowi padania $\alpha$ . Zauważmy, że trójkąty $A D B$ i $A C B$ są trójkątami przystającymi. Oba trójkąty są prostokątne i mają wspólną przeciwprostokątną $A B$ . Bok $A D$ trójkąta $A D B$ jest równy bokowi $B C$ trójkąta $A C B$ – w czasie $\Delta t$ , gdy promień $2$ pokonywał drogę z punktu $C$ do $B$ $|CB|=v\,\Delta t|$ , promień $1'$ przebył odcinek $A D$ z tą samą prędkością, więc $|AD|=v\,\Delta t$ , a co za tym idzie, $|CB|=|AD|$ . Odpowiednie kąty w trójkątach przystających muszą być sobie równe, więc kąt odbicia, który oznaczyliśmy przez $\delta$ , jest równy kątowi padania $\alpha$ . Wykazaliśmy zatem, że

Ponadto z zasady Huygensa wynika, że

Te dwa stwierdzenia stanowią prawo odbicia światła.

Ważną własnością biegu promieni świetlnych jest ich odwracalność. Gdy odwrócimy bieg promienia światła, wówczas promień odbity stanie się promieniem padającym, a padający – odbitym.

Przejdźmy teraz do omówienia prawa załamania światła. Wyprowadzimy je, wychodząc z zasady Huygensa. Najpierw jednak omówimy samo zjawisko załamania światła.

Na granicy dwóch ośrodków część energii promieniowania wraca do pierwszego ośrodka – występuje odbicie światła. Jeżeli drugi ośrodek jest przeźroczysty, to światło może przejść przez granicę ośrodków i wówczas z reguły zmienia kierunek swego biegu. Właśnie to zjawisko nazywamy załamaniem światła.

Ilustracja 8.2. **Pałeczka zanurzona w wodzie wydaje się złamana**

Skutkiem załamania światła jest pozorne zakrzywianie się prostych przedmiotów częściowo zanurzonych w wodzie. Na pewno zauważyłeś, patrząc z boku na łyżeczkę zanurzoną w szklance herbaty, że wydaje się ona załamana na granicy wody i powietrza. To samo dotyczy pałeczki zanurzonej w wodzie (il. 8.2). Te i inne proste obserwacje każą nam sądzić, że przy przejściu z jednego ośrodka do drugiego światło ulega załamaniu.

Doświadczenie pokazowe

Do pokazania biegu promienia padającego, załamanego i odbitego od granicy dwóch ośrodków wykorzystamy wąski promień światła, uzyskany na przykład za pomocą wskaźnika laserowego. Promień kierujemy pod pewnym kątem do płaskościennego naczynia szklanego, np. akwarium, napełnionego częściowo wodą (il. 8.3). Przebieg wiązki światła z latarki można uwidocznić, umieszczając w naczyniu na przykład (nieco ukośnie do pionu) szarą płytkę z tworzywa sztucznego lub kartkę z kartonu. Można również rozpylić nad wodą sproszkowaną kredę szkolną lub puścić nad nią trochę dymu, na przykład z kopcącego knota świecy lub patyczka (nie należy stosować dymu tytoniowego!). Ponadto do wody można dodać trochę fluoresceiny lub zabarwić ją przez dodanie małej ilości innego płynu – płynu do mycia naczyń, herbaty lub mleka. Obserwujemy promień padający, załamany, a także i odbity od powierzchni wody. Zauważamy również, że promień padający, załamany i odbity leżą zawsze we wspólnej płaszczyźnie (w naszym przypadku – w płaszczyźnie praktycznie prostopadłej do powierzchni wody).

Ilustracja 8.3. **Pokaz biegu promienia padającego, załamanego i odbitego**

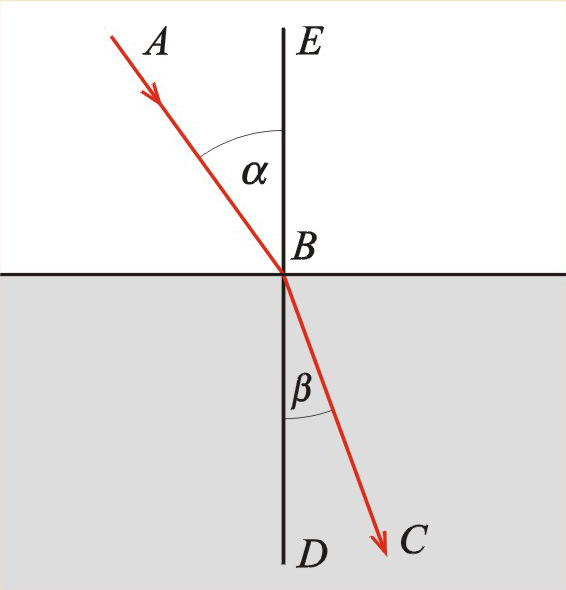
Przebieg wiązki światła padającej na granicę rozdziału ośrodków schematycznie przedstawiono na il. 8.4. Promień $A B$ pada pod kątem $\alpha$ do linii normalnej $D E$ do powierzchni rozdziału ośrodków. Promień przechodzący $B C$ jest załamany względem tej linii pod kątem $\beta$ . Kąt $\alpha$ nazywa się kątem padania, kąt $\beta$ nazywa się kątem załamania. Dla prostoty rysunku pominęliśmy tutaj promień odbity, trzeba jednak pamiętać, że na granicy dwóch ośrodków część światła się odbija (poza szczególnymi przypadkami związanymi ze światłem spolaryzowanym – patrz rozdział 8.9. Polaryzacja światła).

Ilustracja 8.4. **Przebieg wiązki światła padającej na granicę rozdziału ośrodków; zrezygnowano z pokazania promienia odbitego**

Wyprowadzimy teraz prawo załamania światła. Załamanie światła wynika z tego, że prędkość jego rozchodzenia się w różnych ośrodkach jest różna. Oznaczmy przez $v_{1}$ prędkość światła w ośrodku pierwszym i przez $v_{2}$ – w drugim. Niech na płaszczyznę rozdziału ośrodków $M N$ pada płaska fala (il. 8.5). Powierzchnia czoła fali $A C$ jest prostopadła do promieni $1$ i $2$ . W chwili, gdy promień $1$ dociera do powierzchni $M N$ w punkcie $A$ , w drugim ośrodku zaczyna się rozchodzić fala elementarna. Jej promień dotrze do punktu $D$ w tym samym czasie $\Delta t$ , w którym promień $2$ pokona odcinek $C B$ w pierwszym ośrodku. Ze względu na różne prędkości światła w tych ośrodkach długości odcinków $C B$ i $A D$ nie będą jednakowe

$|CB|=v_{1}\Delta t$ , $|AD|=v_{2}\Delta t$

Ilustracja 8.5. Czoło $B D$ fali płaskiej przechodzącej do drugiego ośrodka jest utworzone przez nałożenie się elementarnych fal kulistych rozchodzących się od powierzchni rozdziału ośrodków

Powierzchnię fali przechodzącej otrzymamy, prowadząc płaszczyznę $D B$ styczną do wszystkich wtórnych fal elementarnych, których środki są położone na płaszczyźnie rozdziału $M N$ . Widzimy, że promień $1'$ (prostopadły do powierzchni falowej $D B$ ) będzie załamany w stosunku do promienia $1$ oraz że $\beta\neq\alpha$ . Matematyczny związek między tymi kątami otrzymamy, wykorzystując własności trójkątów prostokątnych: $A B C$ i $A D B$ . Zatem:

|CB|=v_{1}\Delta t=|AB|\sin\alpha

( 8.1 )

|AD|=v_{2}\Delta t=|AB|\sin\beta

( 8.2 )

Po podzieleniu tych równań stronami i uproszczeniu otrzymamy:

\frac{\sin\alpha}{\sin\beta}=\frac{v_{1}}{v_{2}}=n

( 8.3 )

gdzie $n$ jest wielkością stałą dla danych ośrodków – jak widać, niezależną od kąta padania.

Otrzymaliśmy prawo Snelliusa załamania światła, które słowami można wyrazić następująco:

W uzupełnieniu należy podać:

O prawdziwości prawa załamania światła upewnimy się, wykonując doświadczenie „Snellius” (patrz rozdział 8.2. Doświadczenie „Snellius”). Współczynnik załamania światła jest to stała wielkość, charakteryzująca dwa ośrodki, wyrażająca stosunek prędkości światła w jednym ośrodku do prędkości światła w drugim ośrodku:

n_{1,2}=\frac{v_{1}}{v_{2}}

( 8.4 )

Widzimy, że – zgodnie z (8.3) – kąt załamania $\beta$ jest mniejszy od kąta padania $\alpha$ wtedy, gdy światło w ośrodku drugim rozchodzi się wolniej niż w ośrodku pierwszym. Zwróćmy uwagę, że przy odwróceniu biegu światła, gdy przechodzi ono z ośrodka „ $2$ ” do ośrodka „ $1$ ”, posługujemy się współczynnikiem załamania $n_{2,1}$ , będącym odwrotnością $n_{1,2}$ :

n_{2,1}=\frac{1}{n_{1,2}}=\frac{v_{2}}{v_{1}}

Pełna nazwa tak zdefiniowanego współczynnika powinna brzmieć: względny współczynnik załamania, gdyż dotyczy współczynnika załamania jednego ośrodka względem drugiego. Można jednak zdefiniować tzw. bezwzględny współczynnik załamania określonego ośrodka względem próżni. Jest on równy stosunkowi sinusa kąta padania do sinusa kąta załamania przy przejściu promienia z próżni do danego ośrodka, jak również jest równy stosunkowi prędkości światła w próżni $c$ do prędkości światła w danym ośrodku $v$ :

n_{o\acute{s}r}=\frac{c}{v_{o\acute{s}r}}

( 8.5 )

Korzystając ze wzoru (8.4), względny współczynnik załamania światła można wyrazić za pomocą stosunku bezwzględnych współczynników załamania – bezwzględny współczynnik załamania pierwszego ośrodka:

n_{1}=\frac{c}{v_{1}}

a drugiego ośrodka:

n_{2}=\frac{c}{v_{2}}

więc

n_{1,2}=\frac{v_{1}}{v_{2}}=\frac{n_{2}}{n_{1}}

Znając bezwzględny współczynnik załamania dla danego ośrodka, ze wzoru (8.5) możemy obliczyć, ile wynosi prędkość światła w tym ośrodku. Prędkość ta zależy od stanu fizycznego ośrodka, jego gęstości i temperatury, a także od częstotliwości fali świetlnej (więc i od jej długości). Zwykle w danym ośrodku światło o mniejszej częstotliwości (większej długości fali) rozchodzi się szybciej od światła o wyższej częstotliwości (mniejszej długości fali), więc światło czerwone (duża długość fali) rozchodzi się szybciej od zielonego (średnia długość fali), a zielone szybciej od fioletowego (mała długość fali). Dlatego w tablicach wartości współczynników załamania podaje się, jakiego światła dotyczą i w jakim stanie znajduje się ośrodek.

Ponieważ w większości przypadków określa się współczynnik załamania w stosunku do powietrza, więc trzeba wiedzieć, ile wynosi współczynnik załamania powietrza względem próżni. Prędkość światła w powietrzu nieznacznie różni się od prędkości światła w próżni, dlatego bezwzględny współczynnik załamania powietrza nieznacznie różni się od jedności, np. w normalnych warunkach dla żółtego światła (lampy sodowej, $\lambda=589\, nm$ ) wynosi $n_{p}=1,000292$ . Zatem dla dowolnego ośrodka bezwzględny współczynnik załamania $n_{o\acute{s}r}$ jest w przybliżeniu równy współczynnikowi załamania $n$ względem powietrza:

n=\frac{n_{o\acute{s}r}}{n_{p}}\approx n_{o\acute{s}r}

( 8.6 )

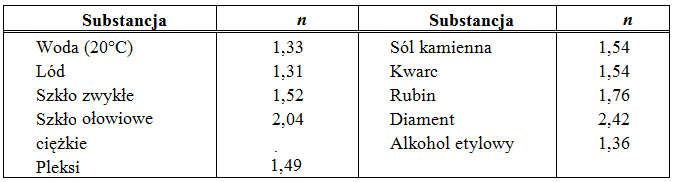
Wartości współczynnika załamania względem powietrza dla niektórych substancji podane są w tabeli na il. 8.6.

Rozważmy teraz szczególnie ciekawy przypadek, mający ważne zastosowanie praktyczne – tzw. całkowite odbicie. Jeżeli promień światła pada na ośrodek optycznie gęstszy, czyli o współczynniku załamania $n>1$ , to zgodnie ze wzorem (8.3) promień załamuje się w ten sposób, że kąt załamania jest mniejszy od kąta padania $\beta \less \alpha$ – il. 8.7a). Jeżeli promień będzie się poruszał w przeciwną stronę, z ośrodka optycznie gęstszego do rzadszego (il. 8.7b), to sytuacja będzie odwrotna. Kąty „zamienią się rolami” – teraz kąt padania będzie mniejszy od kąta załamania $\alpha \less \beta$ i prawo załamania przybierze postać:

\frac{\sin\alpha}{\sin\beta}=\frac{v_{2}}{v_{1}}=\frac{1}{n}

( 8.7 )

Jeżeli będziemy zwiększać kąt padania, to przy pewnej jego wartości $\alpha_{0}$ kąt załamania będzie równy $90^{\circ}$ (8.6c). Wtedy, zgodnie z (8.7):

\sin\alpha_{0}=\frac{1}{n}

( 8.8 )

Ilustracja 8.7. **Kąty odbicia i załamania**

a) kąt padania jest większy od kąta załamania przy przejściu promienia do ośrodka gęstszego optycznie, b) sytuacja jest odwrotna przy odwróconym biegu promienia, c) przy dostatecznie dużym kącie padania $\alpha_{0}$ kąt załamania jest równy $90^{\circ}$ , d) przy kącie padania $\alpha>\alpha_{0}$ następuje całkowite odbicie od powierzchni rozdziału ośrodków

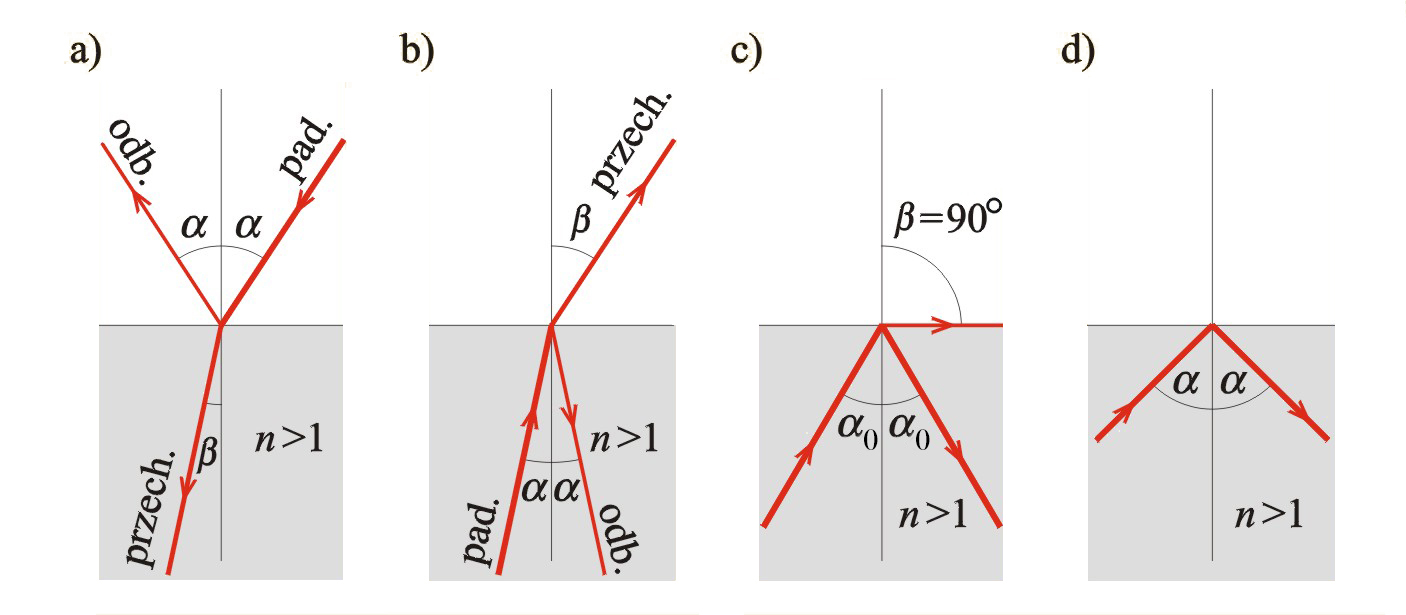
Kąt padania $\alpha_{0}$ odpowiadający warunkowi (8.8) nazywa się kątem granicznym. Wystarczy teraz tylko nieznacznie przekroczyć ten kąt, a promień nie będzie miał możliwości przejść do drugiego ośrodka. Wtedy nastąpi całkowite odbicie – promień odbije się od powierzchni rozdziału ośrodków pod kątem równym kątowi padania (il. 8.7d).

Należy zwrócić uwagę na to, że nie dzieje się tak, że przy zwiększaniu kąta padania promień przechodzi do drugiego ośrodka całkowicie pod coraz większym kątem załamania, aż raptem dla $\alpha=\alpha_{0}$ ginie promień załamany i pojawia się promień odbity. W rzeczywistości na granicy dwóch ośrodków wiązka padająca dzieli się na dwie – odbitą i załamującą się (wzory na zależność natężenia każdej z tych wiązek od kąta padania i współczynnika załamania są dość złożone i dlatego nie będziemy ich wyprowadzać). Zgodnie z prawem zachowania energii natężenie (patrz rozdział 5.9. Energia i natężenie fali) promienia padającego jest równe sumie natężeń promienia przechodzącego i odbitego (il. 8.7):

I_{pad}=I_{przech}+I_{odb}

W miarę zwiększania kąta padania wzrasta natężenie promienia odbitego i maleje natężenie promienia załamanego. Przy zbliżaniu się kąta padania do kąta granicznego natężenie promienia załamanego zbliża się do zera, a natężenie promienia odbitego zbliża się do natężenia promienia padającego (il. 8.7c). Przy przechodzeniu przez kąt graniczny nie ma żadnej skokowej zmiany!

Całkowite odbicie wykorzystuje się w technice światłowodowej. Cienkie włókna szklane lub ze sztucznych polimerów – stanowią one rdzeń światłowodu – pokrywa się warstewką materiału o współczynniku załamania mniejszym niż współczynnik załamania rdzenia. Na skutek wielokrotnego całkowitego odbicia promień światła może się poruszać wzdłuż prostego lub zgiętego włókna. Włókna kompletuje się w wiązki, które mogą przenosić obrazy po drodze zakrzywionej. Każde włókno w wiązce przenosi tylko mały fragment obrazu. Takie światłowody wykorzystuje się w medycynie do obserwacji trudno dostępnych wewnętrznych organów, np. podczas operacji chirurgicznej. Światłowody znalazły także zastosowanie do przenoszenia sygnałów cyfrowych w sieci Internet oraz w telefonii i telewizji.

Pytania i problemy

Podaj podstawowe dwa prawa dotyczące odbicia i załamania światła. Z jakiej zasady ruchu falowego one wynikają?
Co to jest współczynnik załamania i jakim wzorem się wyraża? Czym się różni absolutny od względnego współczynnika załamania? Podaj wzór wiążący te dwa typy współczynników.
Co to jest całkowite wewnętrzne odbicie i kąt graniczny? Podaj przykład zastosowania zjawiska całkowitego wewnętrznego odbicia.
Na granicę między powietrzem i cieczą pada światło pod kątem $\alpha=50^{\circ}$ . Stwierdzono, że promienie: wchodzący do cieczy i odbity od jej powierzchni są do siebie prostopadłe. Oblicz bezwzględny współczynnik załamania tej cieczy.