2.10. Dodatek: Model gazu elektronowego (temat nadobowiązkowy)
Główne założenia modelu
Model, który tu przedstawimy, jest bardzo uproszczony. Mimo to pozwala za pomocą elementarnych metod wyjaśnić wiele zjawisk zachodzących w metalach i półprzewodnikach.
Zbiór swobodnych elektronów w metalu potraktujemy jako gaz doskonały, zwany gazem elektronowym. W przewodnikach wykonanych z metali, takich jak na przykład miedź (jednowartościowa), w jednostce objętości jest tyle samo swobodnych elektronów (tzw. elektronów przewodnictwa), ile jest w niej atomów, ponieważ każdy atom sieci krystalicznej pozbywa się jednego elektronu, sam stając się dodatnim jonem. W przypadku miedzi koncentracja elektronów (czyli liczba elektronów mieszczących się w jednostce objętości) wynosi . Swoboda poruszania się elektronów jest ograniczona tylko do obszaru przewodnika, ponieważ dodatnie jony sieci tworzą wspólne pole, które utrudnia elektronom ucieczkę. W ten sposób elektrony w metalu znajdują się jak gdyby w pojemniku.
Przyjmiemy, że elektrony są w nieustannym chaotycznym ruchu i przy zderzeniach z jonami sieci doznają przypadkowych gwałtownych zmian prędkości i kierunku swojego ruchu (można wykazać, że wzajemne zderzenia między elektronami zdarzają się rzadko). Zderzenia te przypominają zderzenia cząsteczek w zwykłym gazie zamkniętym w zbiorniku. Dla średniej energii kinetycznej elektronów stosujemy takie samo równanie, jak dla energii kinetycznej cząsteczek gazu doskonałego (tom II, rozdział 6.8. Podstawowe równanie teorii kinetycznej gazów a równanie Clapeyrona), wzór:
Stąd możemy oszacować średnią prędkość elektronów w temperaturze pokojowej . Zgodnie z wartościami tablicowymi przyjmiemy, że stała Boltzmanna wynosi , a masa elektronu . Zatem:
Widzimy, że w stosunku do „zwykłych” prędkości jest to duża prędkość, gdyż wynosi 100 km/s, ale jest trzy tysiące razy mniejsza od prędkości światła.
Wyprowadzenie prawa Ohma
Co się dzieje z elektronami, gdy włączymy pole elektryczne? Czy pole zmieni ich chaotyczny ruch na uporządkowany? Nie – uporządkowany ruch tylko nieznacznie zmodyfikuje chaotyczny ruch elektronów, gdyż średnia prędkość uporządkowanego ruchu w kierunku pola jest o około razy mniejsza od średniej prędkości ruchu chaotycznego (patrz Przykład 7). Spójrz na il. 2.35. Niech czerwona linia przedstawia „tor” elektronu w gazie elektronowym pod nieobecność pola. Wówczas jego ruch w obecności pola będzie wyobrażony przez linię niebieską (w przybliżeniu – linia łamana). W efekcie wielu zderzeń elektron znajdzie się w miejscu , zamiast w miejscu , gdzie trafiłby przy braku pola. Dozna zatem przesunięcia wypadkowego .

W polu o natężeniu elektrony doznają działania siły i uzyskują przyśpieszenie na odcinku drogi swobodnej między zderzeniami. W czasie ruchu na drodze swobodnej elektron nabywa w kierunku pola prędkości . Przy każdym zderzeniu traci tę prędkość, po czym na następnym odcinku znowu nabywa ją od pola prędkości, ale ma ona wówczas inną wartość. Średnia prędkość elektronu w kierunku pola nazywa się prędkością unoszenia lub prędkością dryfu (dryftu). Odcinki drogi swobodnej mają różne, zupełnie przypadkowe długości. Dodatkowe przesunięcia elektronu w polu wynoszą:
, itd.
Wszystkie przesunięcia mają ten sam kierunek i zwrot (taki jak przyspieszenie ), dlatego po dłuższym czasie elektron dozna przesunięcia:
Średnia prędkość ruchu uporządkowanego elektronu wyniesie:
gdzie
nazywamy średnim czasem swobodnego przelotu elektronu. Ponieważ , więc:
Prędkość dryftu jest ważną wielkością fizyczną, gdyż za jej pomocą można wyrazić natężenia prądu elektrycznego oraz gęstości prądu . Wiemy, że natężenie wyraża się wzorem:
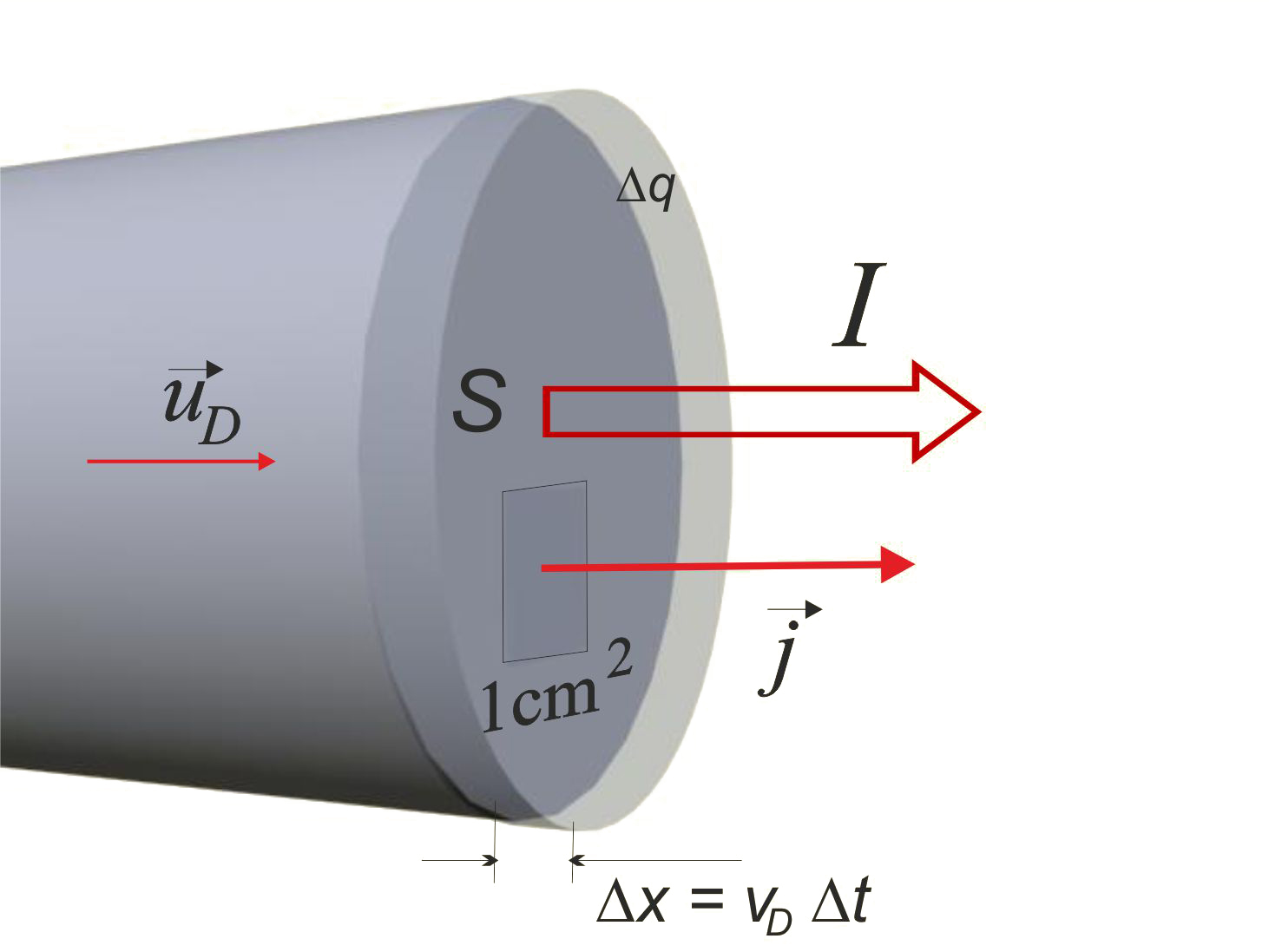
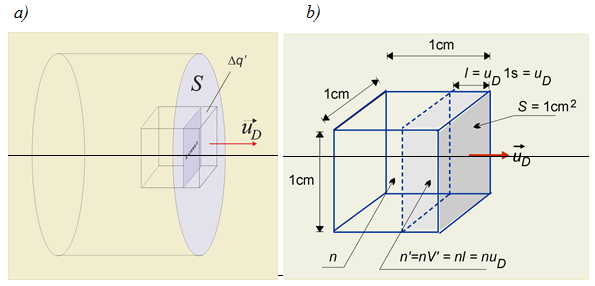
Prąd elektryczny w przewodniku to przepływ sumarycznego ładunku, na który składają się pojedyncze ładunki elektronów . Czyli natężenie prądu można wyrazić za pomocą – sumarycznego ładunku elektronów przepływających przez przekrój przewodnika w jednostkowym czasie , Widzimy na il. 2.36, że ten ładunek zawarty jest w zacieniowanym obszarze cylindrycznego przewodnika o objętości .
W jednostkowej objętości przewodnika znajduje się elektronów swobodnych, dlatego w objętości będzie ich . Zatem sumaryczny ładunek
Po podstawieniu tu , otrzymamy:
Po podstawieniu do wzoru (2.52) mamy:
Teraz możemy już łatwo obliczyć gęstość prądu. Przypomnijmy sobie, co to jest gęstość prądu. Średnia gęstość prądu jest to stosunek natężenia prądu do pola przekroju poprzecznego przewodnika:
czyli gęstość prądu jest równa natężeniu prądu przepływającemu przez jednostkowy przekrój przewodnika (np. ):
Po podstawieniu prędkości ze wzoru (2.51) mamy:
Widzimy, że gęstość prądu zależy wprost proporcjonalnie od natężenia pola , gdyż współczynnik przy jest stały (czas praktycznie nie zależy od ). Wprowadzając oznaczenie:
możemy wzór (2.58) zapisać w postaci:
Bardzo łatwo możemy się przekonać, że jest to prawo Ohma wyrażone w innej niż (2.9) postaci (jest to tzw. lokalna postać prawa Ohma). Natężenie jednorodnego pola w prostoliniowym przewodniku o długości , na którego końcach panuje napięcie , wynosi (wzór (1.29)). Gęstość prądu w przewodniku o powierzchni przekroju poprzecznego wynosi . Po podstawieniu tych dwóch wzorów do (2.59) oraz przyjęciu, że , otrzymamy znane nam równanie (2.9) przedstawiające prawo Ohma:
skąd
Wykorzystaliśmy tu wzór (2.10) na opór przewodnika: (stały współczynnik we wzorze (2.60) oznaczony został symbolem nie bez przyczyny, gdyż odgrywa on w prawie Ohma rolę przewodności właściwej, czyli odwrotności oporu właściwego, ).
Widzimy, że – korzystając z modelu gazu elektronowego – teoretycznie byliśmy w stanie wyprowadzić jeden z podstawowych wzorów doświadczalnych dla prądu elektrycznego – prawo Ohma. Jednakże model ten oddaje rzeczywistość tylko w sposób przybliżony i w przypadku bardziej skomplikowanych zagadnień zawodzi. Jest on bowiem oparty na klasycznej fizyce i nie uwzględnia współczesnej wiedzy z zakresu mechaniki kwantowej.
Przykład 7
W drucie miedzianym o średnicy płynie prąd o natężeniu . Jaka jest średnia prędkość unoszenia elektronów?
Rozwiązanie: Ze wzoru (2.56) mamy:
Gęstość prądu wynosi:
Zatem:
Podstawiając tu koncentrację elektronów w miedzi oraz pozostałe wielkości liczbowe, otrzymamy:
zatem:
Widzimy, że jest to prawdziwie żółwie tempo! W ciągu 10 sekund elektrony przebywają niecały milimetr. Jednakże prędkości unoszenia elektronów nie należy identyfikować z prędkością rozchodzenia się zmian pola elektrycznego wzdłuż drutu. Ta ostatnia jest rzędu prędkości światła. Po włączeniu pola do obwodu elektrycznego elektrony startują prawie natychmiast w całym obwodzie, nawet w najdalszych jego miejscach. Dlatego po włączeniu przełącznika lampa pod sufitem zapala się natychmiast, chociaż w czasie jej świecenia elektrony przemieszczają się przez włókno żarówki w „żółwim” tempie.
Przykład 8
Oblicz średni czas swobodnego przelotu elektronu na odcinku drogi swobodnej w drucie miedzianym. Koncentracja elektronów swobodnych wynosi , a opór właściwy miedzi wynosi .
Rozwiązanie: Ponieważ zgodnie ze wzorem (2.11) opór właściwy jest odwrotnością przewodnictwa właściwego, , więc ze wzoru (2.59) mamy:
Stąd
Zatem:
Elektron w gazie elektronowym doznaje:
zderzeń w czasie jednej sekundy. W naszym przykładzie mamy więc:
Pytania i problemy
- Scharakteryzuj gaz elektronowy.
- Wytłumacz, dlaczego elektrony stanowiące gaz elektronowy i poruszające się z bardzo dużymi prędkościami nie uciekną z przewodnika.
- Wiemy, że elektron jest lżejszy od przeciętnego atomu kilkadziesiąt tysięcy razy. Ile razy średnia prędkość elektronu w gazie elektronowym przewyższa średnią prędkość cząsteczek w zwykłym gazie w tej samej temperaturze?
- Wyjaśnij, na czym polega modyfikacja ruchu elektronów w metalu następująca, gdy włączymy pole elektryczne i przez przewodnik popłynie prąd.
- Co rozumiemy przez prędkość unoszenia elektronów w przewodniku? Oszacuj, ile razy średnia prędkość chaotycznego ruchu elektronów jest większa od prędkości unoszenia.
- Wyjaśnij, dlaczego żarówka zaczyna świecić prawie natychmiast po zamknięciu wyłącznika, mimo że prędkość unoszenia elektronów w przewodniku jest bardzo mała.
- Dany jest ładunek elektronu , koncentracja elektronów oraz ich prędkość unoszenia. Napisz równania przedstawiające zależność gęstości prądu w metalach od koncentracji elektronów swobodnych i prędkości unoszenia.
- Na podstawie prawa Ohma wyprowadź związek między gęstością prądu i natężeniem pola elektrycznego.
- Natężenie pola elektrycznego wewnątrz metalu umieszczonego w polu elektrostatycznym ma wartość zero. Dlaczego nie znika pole elektryczne w przewodniku, przez który płynie prąd? Wskazówka: Rozważ podobieństwa i różnice między sytuacja elektrostatyczną a dynamiczną – gdy płynie prąd w przewodniku.
- Zastanów się, czy można by przyjąć konwencję, że elektrony mają ładunek dodatni, a protony – ujemny. Wyjaśnij, jaki miałoby to wpływ na określanie kierunku przepływu prądu.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
