2.8. Prawa Kirchhoffa
Niektórych układów oporników nie da się przedstawić jako kombinacji tylko szeregowego i równoległego połączenia. W bardziej skomplikowanych obwodach możemy mieć ponadto do czynienia nie z jednym, ale z kilkoma źródłami napięcia. Cały obwód można wtedy przedstawić w postaci pojedynczych obwodów zamkniętych – tzw. oczek – i punktów rozgałęzienia – tzw. węzłów (il. 2.18). Wtedy przychodzą nam z pomocą prawa Kirchhoffa.

Twierdzenie o punkcie rozgałęzienia wynika z prawa zachowania ładunku. Jeżeli w określonym czasie do węzła dopływa określona ilość ładunku, to tyle samo ładunku musi go opuść (gdyż ładunek ani nie znika, ani nie tworzy się z niczego, chyba że gromadziłby się w węźle, ale takiej możliwości przy przepływie prądu w przewodnikach nie ma). Innymi słowy: tyle samo prądu dopływa do węzła, ile z niego wypływa (il. 2.19).

Twierdzenie o obwodzie zamkniętym wynika z prawa zachowania energii, gdyż tylko wtedy praca wykonana przez siły postronne w źródle (źródłach) prądu jest zbilansowana z ciepłem Joule'a-Lenza. Widzieliśmy to na przykładzie prostego obwodu, gdy wyprowadzaliśmy dla niego prawo Ohma. Przyjrzyjmy się bliżej zmianom potencjału w prostym obwodzie, w którym mamy tylko jedno źródło napięcia i jeden opór zewnętrzny (il. 2.20a; niebieska strzałka wskazuje kierunek przepływu prądu i kierunek zmian potencjału). Zgodnie z drugim prawem Kirchhoffa algebraiczna suma napięć (różnic potencjałów związanych z oporem wewnętrznym źródła i z oporem zewnętrznym ) i siły elektromotorycznej musi być równa zeru, czyli:
lub
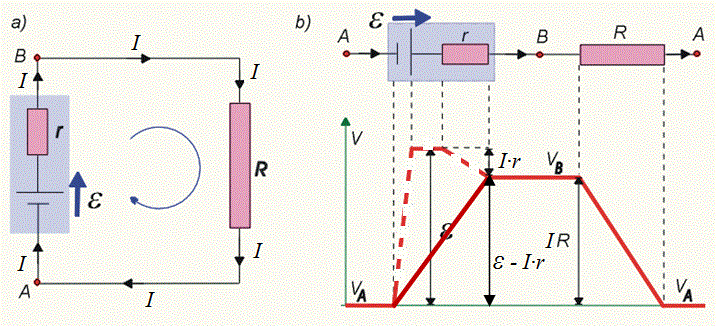
Przebieg zmian potencjału jest pokazany na il. 2.20b. Dla ułatwienia nad wykresem zmian potencjału umieszczono ten sam obwód, ale w postaci rozwiniętej – zaczyna się i kończy w tym samym punkcie (oczywiście, nie jest on otwarty!). Jak widać, wzrost potencjału wywołany przez SEM jest skompensowany spadkiem potencjału związanym z oporami i . Zauważmy, że napięcie na zaciskach SEM będzie mniejsze od wartości – wspominaliśmy o tym w rozdziale 2.7. Obwody prądu stałego. W punkcie mamy potencjał (który możemy umownie przyjąć za równy zeru). Siła elektromotoryczna powoduje, że ładunki – przechodząc z punktu do punktu – znajdą się w miejscu o wyższym potencjale , jednakże, jak widać na wykresie, część wartości zostanie „zużyta” w związku z oporem wewnętrznym źródła. Dlatego potencjał w punkcie jest niższy od o , . Oczywiście, tak jest tylko w przypadku przepływu prądu. Wtedy różnica potencjałów na zaciskach i źródła obciążonego odbiornikiem o oporze zamykającym obwód jest mniejsza od . Gdy źródło znajduje się w obwodzie niezamkniętym, prąd nie płynie i nie ma żadnego spadku potencjału związanego z oporem wewnętrznym, czyli . Wtedy cała wartość występuje na zaciskach źródła.
Przykład 1
W celu uzyskania podwyższonej SEM łączymy szeregowo (tak jak na il. 2.21) kilka ogniw. Uzyskujemy wtedy baterię ogniw, która może zasilać określone urządzenie o oporze (il. 2.21).

Ile wynosi wypadkowa SEM takiej baterii oraz natężenie prądu płynącego przez opornik w sytuacji, gdy ogniwa są jednakowe.
Rozwiązanie: Łączenie szeregowe ogniw w wersji „plus do minusa” (il. 2.21) powoduje, że SEM tych ogniw dodają się. Wypadkowa SEM jest wtedy sumą SEM ogniw składowych:
Na mocy II prawa Kirchhoffa możemy napisać, że:
Oznaczyliśmy tu opory wewnętrzne ogniw za pomocą symboli , , …, . Zgodnie ze wzorem (2.32) równanie (2.33) przyjmie postać:
Zauważamy jednak, że opory wewnętrzne ogniw dodają się, co na ogół nie jest pożądanym efektem.
Gdy mamy do czynienia z jednakowymi ogniwami o SEM i oporze każde, to natężenie prądu płynącego w obwodzie możemy wyrazić jako:
Widać, że uzyskujemy tym większe natężenie , im więcej połączymy ogniw – przekształćmy wyrażenie (2.34):
Mianownik wyrażenia (2.36) staje się coraz mniejszy dąży do zera), w miarę wzrostu , zatem całe rośnie.
Przykład 2
Gdy chcemy naładować akumulator (np. akumulator samochodowy czy akumulatorek do aparatu fotograficznego) o SEM (i oporze ), to łączymy go z ładowarką o większej SEM (i oporze ), ale w taki sposób, że łączymy przeciwne bieguny tych źródeł prądu. Do regulacji natężenia prądu ładowania w obwód wkładamy potencjometr o nominalnym oporze (il. 2.22).
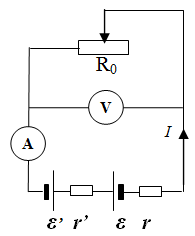
Przyjmij, że podczas ładowania akumulatorka o pojemności 2400 mAh w obwodzie jak wyżej, wartości parametrów były stałe i wynosiły: , , , , , . Oblicz, jaka część potencjometru była włączona w obwód oraz czas ładowania akumulatorka, przy założeniu, że przed ładowaniem był on praktycznie całkowicie wyczerpany.
Rozwiązanie: Na mocy II prawa Kirchhoffa możemy zapisać:
Sile elektromotorycznej przypisaliśmy w tym równaniu znak minus, gdyż ładowane ogniwo jest włączone w oczko w taki sposób, że prąd w jego wnętrzu płynie od bieguna dodatniego do ujemnego. Taki przepływ prądu wewnątrz ogniwa zapewnia, że część energii wydzielonej w ogniwie jest „zużywana” na jego naładowanie, czyli na odwrócenie tych reakcji chemicznych, które zapewniały pracę ogniwa naładowanego, zanim się wyczerpało.
Symbolem oznaczyliśmy tutaj opór tej części potencjometru, przez którą płynie prąd, zatem szukana część to iloraz .
Z równania (2.37) możemy wyliczyć :
Widać więc, że w obwodzie było wykorzystanych całkowitego oporu .
Pojemność akumulatora (nie mylić z pojemnością kondensatora!) to ilość ładunku , jaką może przez swoje wnętrze przenieść ten akumulator bez istotnego zmniejszenia jego SEM. Pojemność ta jest jednak podawana nie w kulombach, lecz w jednostkach będących iloczynem jednostek natężenia prądu (ampery, miliampery) i czasu (wyrażanego najczęściej w godzinach). Jest to wygodna jednostka, gdyż pozwala zapisać związek:
i stąd łatwo obliczyć:
Przykład 3
Zamierzamy zasilić opornik dwiema identycznymi bateriami o SEM i oporze . Baterie te możemy połączyć szeregowo (il. 2.23a) lub równolegle (il. 2.23b). Zbadaj, które z połączeń zapewni zasilenie opornika prądem o większym natężeniu.

Rozwiązanie: W obwodzie z szeregowym połączeniem ogniw płynie prąd o natężeniu , danym wzorem wynikającym z równania (2.34):
W obwodzie z połączeniem równoległym opornik jest zasilany prądem o natężeniu , na który składają się dwa prądy o natężeniu . Jest to zgodne z I prawem Kirchhoffa oraz z faktem, że baterie są identyczne. Możemy więc zapisać, zgodnie z II prawem Kirchhoffa zastosowanym do jednego z oczek zawierających opór :
Równanie to pozwala wyznaczyć :
Zwróćmy uwagę, że wyrażenie to pokazuje, iż wypadkowa SEM dwóch jednakowych baterii połączonych równolegle jest równa SEM każdej z nich. Jednak wypadkowy opór wewnętrzny tych baterii jest równy połowie oporu wewnętrznego każdej – to właśnie jest zaletą równoległego łączenia baterii.
By zbadać, który z prądów ma większe natężenie, postawmy hipotezę, że . Sprawdzimy teraz, czy i pod jakim warunkiem jest ona prawdziwa.
Po przekształceniu tego wyrażenia otrzymamy wyrażenie matematycznie równoważne:
Oznacza to, że gdy dwiema bateriami zasilamy opornik o oporze większym niż opór wewnętrzny jednej z nich, korzystniej jest połączyć baterie szeregowo i uzyskać zwiększoną SEM. Gdy jednak opór jest mniejszy od , to korzystniej jest połączyć te baterie równolegle i uzyskać obniżenie oporu wewnętrznego.
Przykład 4
Na il. 2.24 przedstawiono obwód zawierający dwa źródła SEM o parametrach, odpowiednio, , i , , oraz trzy oporniki o oporach , , . Wyznacz natężenia prądu płynącego we wszystkich gałęziach obwodu i napięcia związane z oporami zewnętrznymi.

Rozwiązanie: Z praw Kirchhoffa otrzymamy trzy równania – jedno dla natężeń prądu i dwa dla oczek zaznaczonych na rysunku:
Na rysunku zaznaczono spodziewane kierunki przepływu prądu. Nie musimy się przejmować tym, że mogliśmy się pomylić i zaznaczyć niewłaściwy kierunek. W takim przypadku rozwiązanie układu równań da właściwą wartość natężenia, ale ze znakiem ujemnym.
Po rozwiązaniu układu równań otrzymamy:
Po podstawieniu wartości liczbowych otrzymamy:
, ,
Na poszczególnych oporach mamy następujące napięcia:
Przykład 5
Obwód składa się z oporników o jednakowych oporach rozmieszczonych na krawędziach sześcianu (il. 2.25a). Oblicz opór wypadkowy, przyjmując, że prąd wpływa do wierzchołka sześcianu, a wypływa z wierzchołka .

Rozwiązanie: Symetria układu oporów ułatwi nam rozwiązanie zadania. Prąd wpływający musi się rozgałęzić, zgodnie z pierwszym prawem Kirchhoffa, na trzy prądy (patrz il. 2.25a). Symetria sześcianu narzuca równość natężeń prądów – każdy z rozgałęzionych prądów napotyka na jednakowy opór w swojej gałęzi, więc . Trzy oporniki na wejściu są połączone jednym końcem – występuje tam wspólny potencjał . Jednakowe prądy w każdej gałęzi muszą dać jednakowe zmiany potencjału, zgodnie ze wzorem:
Zatem potencjał na przeciwległych końcach tych trzech oporników jest jednakowy i wynosi (widoczne to jest na il. 2.25b, gdzie oporniki zostały rozłożone na płaszczyźnie). Jednakowy potencjał na końcach tych oporników wystąpiłby również wtedy, gdyby oporniki były połączone końcami . Zatem jest to równoważne połączeniu równoległemu tych oporników. Dalszych sześć oporników jest połączonych parami z tymi trzema w punktach, gdzie występuje potencjał . Po drugiej stronie oporniki są połączone w równoważnych punktach , gdzie panuje wspólny potencjał . Zatem te oporniki możemy również potraktować tak, jakby były połączone równolegle. Strona układu jest równoważna stronie ze względu na symetrię, zatem trzy oporniki podłączone do punktu można także traktować tak, jakby były połączone równolegle. W wyniku naszego rozumowania możemy zaproponować układ zastępczy, jak na il. 2.26, który jest równoważny połączeniu oporników w sześcianie.

Obliczenie oporu wypadkowego nie sprawi nam teraz kłopotu. Mamy połączenie szeregowe trzech układów równoległych oporników. Zatem:
Pytania i problemy
- Podaj treść I prawa Kirchhoffa. Jaka zasada jest podstawą tego prawa?
- W punkcie rozgałęzienia, tzw. węźle, spotykają się trzy przewody. W jednym z nich wpływa do węzła prąd , w drugim wypływa z węzła prąd . Jak duży prąd płynie w trzecim przewodzie i w którym kierunku – dopływa czy wypływa z węzła?
- Podaj treść II prawa Kirchhoffa. Jaka zasada jest podstawą tego prawa?
- Wyraź maksymalną wartość natężenia prądu , jaką moglibyśmy osiągnąć w obwodzie z przykładu (Przykład 1), gdybyśmy umieścili w baterii nieskończenie wiele ogniw.
- Wykaż, że sprawność obwodu z przykładu (Przykład 1), rozumiana jako stosunek mocy wydzielanej na oporniku do mocy wydzielanej na oporze wewnętrznym baterii , maleje wraz ze wzrostem liczby ogniw w baterii.
- Wykaż, że równoległe połączenie dwóch różnych baterii, o SEM
i
oraz o oporach
i
da, z punktu widzenia zewnętrznego oporu
, taki sam efekt jak zasilenie go jedną baterią SEM
o wewnętrznym oporze
danymi wzorami:
oraz


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
