5.4. Energia oscylatora harmonicznego

W czasie wykonywania drgań ciało zmienia ciągle swoją prędkość, zmienia się więc i energia kinetyczna ciała. Jeżeli zaniedbamy rozpraszanie energii ciała, to możemy stwierdzić, że całkowita energia ciała drgającego jest stała. Zatem, jeżeli prędkość ciała maleje, to maleje jego energia kinetyczna i musi rosnąć jego energia potencjalna, i na odwrót – jeżeli rośnie jego prędkość i energia kinetyczna, to energia potencjalna maleje. Zatem ciało wykonujące drgania cały czas doznaje przemiany energii kinetycznej w energię potencjalną, i na odwrót.

Omawianie energii ciała wykonującego drgania podzielimy na dwie części – energię kinetyczną i potencjalną.

Energia kinetyczna $E_{k}=\frac{mv^{2}}{2}$ . W ruchu drgającym harmonicznym $v=\omega A\cos\omega t$ (wzór (5.7)), więc:

E_{k}=\frac{mv^{2}}{2}=\frac{1}{2}m\omega^{2}A^{2}\cos^{2}\omega t

Wykorzystując wzór (5.14): $k=m\omega^{2}$ , otrzymamy:

E_{k}=\frac{mv^{2}}{2}=\frac{1}{2}kA^{2}\cos^{2}\omega t

( 5.25 )

Jeżeli ciało w ruchu drgającym jest wychylone z położenia równowagi o $x$ , to działa na nie siła zwrotna (kwazisprężysta) $F=-kx$ i (podobnie jak w przypadku naciągniętej sprężyny) ciało ma energię potencjalną wyrażoną za pomocą wzoru $E_{p}=k\frac{x^{2}}{2}$ (tom II, rozdz. 3.2 Energia potencjalna wzór (3.8)). Teraz $x=A\sin\omega t$ , więc:

E_{p}=k\frac{x^{2}}{2}=\frac{1}{2}kA^{2}\sin^{2}\omega t

( 5.26 )

Porównując wzory (5.25) i (5.26), zauważamy, że gdy energia kinetyczna jest największa, energia potencjalna jest równa zeru, i na odwrót – gdy energia potencjalna jest największa, energia kinetyczna wynosi zero. W każdej chwili całkowita energia $E$ , czyli suma energii kinetycznej i potencjalnej, jest stała, gdyż po dodaniu tych dwóch wyrażeń do siebie otrzymamy:

E=E_{k}+E_{p}=\frac{1}{2}kA^{2}

( 5.27 )

(gdyż wiadomo, że $\sin^{2}\alpha+\cos^{2}\alpha=1$ ). Ponieważ $k=m\omega^{2}$ , mamy również:

E=\frac{1}{2}m\omega^{2}A^{2}

( 5.28 )

Wykresy energii w ruchu harmonicznym przedstawione są na il. 5.10.

Ilustracja 5.10. **Zależność od czasu**

a) energii potencjalnej (linia czarna), energii kinetycznej (linia czerwona) i energii całkowitej (linia zielona), b) wychylenia $x$ (linia czarna), prędkości (linia czerwona). Należy zauważyć, że okres zmian energii kinetycznej i potencjalnej jest dwa razy mniejszy od okresu zmian wychylenia i prędkości

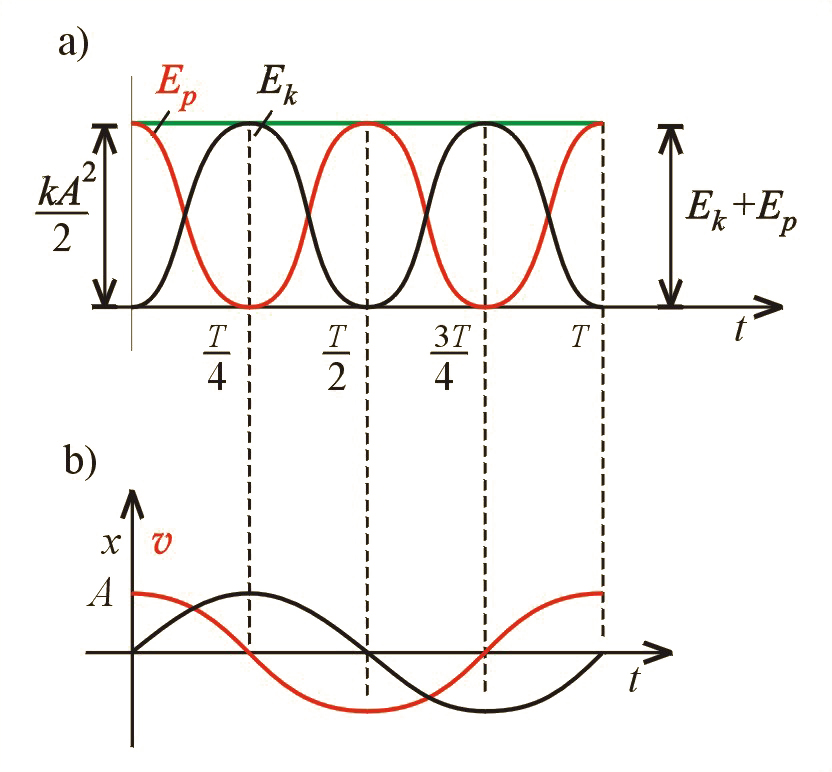
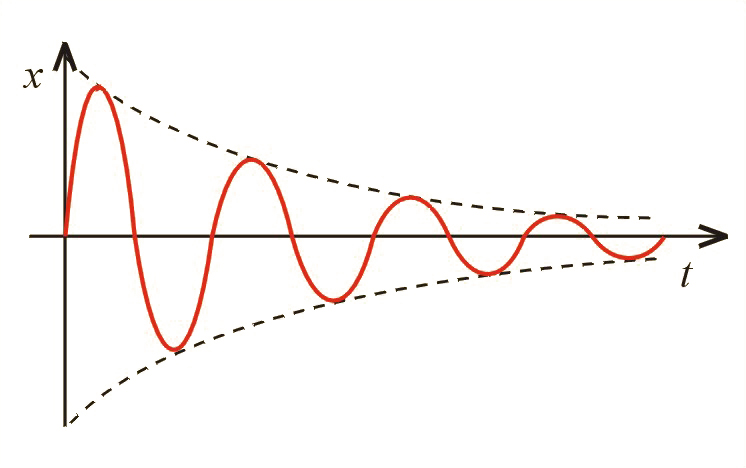
Wzór (5.28) wskazuje, że energia całkowita oscylatora harmonicznego jest proporcjonalna do kwadratu amplitudy drgań. Oczywiście, całkowita energia oscylatora jest stała w czasie tylko wtedy, gdy nie ma rozpraszania energii (np. na tarcie, również na emisję fali). Na skutek rozpraszania energia drgań maleje. Przy malejącej energii maleje amplituda drgań (il. 5.11), mamy wtedy do czynienia z drganiami tłumionymi lub gasnącymi. Przykładem drgań gasnących może być ruch rozbujanej i pozostawionej samej sobie huśtawki.

Ilustracja 5.11. **Zależność wychylenia od czasu w drganiu tłumionym**

Wykres zależności wychylenia od czasu, linią przerywaną zaznaczono tzw. obwiednię drgania, która opisuje zmianę amplitudy drgań w czasie

Pytania i problemy

Opisz przemiany energii w ruchu harmonicznym. Przedstaw i objaśnij równanie opisujące całkowitą energię oscylatora harmonicznego.
W pewnej fazie drgania harmonicznego wychylenie ciała z położenia równowagi stanowi połowę amplitudy drgań. Oblicz, jaką część prędkości maksymalnej stanowi prędkość ciała w tym momencie.