6.2. Prosty obwód prądu przemiennego
Prąd przemienny zachowuje się w tym samym obwodzie inaczej niż prąd stały. Obecność cewki indukcyjnej wpływa silniej na wartość natężenia prądu zmiennego. Dla prądu stałego kondensator tworzy przeszkodę nie do przebycia, gdyż stanowi dla niego przerwę w obwodzie. Natomiast prąd przemienny może płynąć w obwodzie z kondensatorem.
Opór czynny
Do źródła prądu przemiennego o sile elektromotorycznej (6.3):
podłączmy odbiornik o zwykłym oporze . Powstanie obwód elektryczny taki jak na il. 6.3, w którym popłynie prąd przemienny o natężeniu .
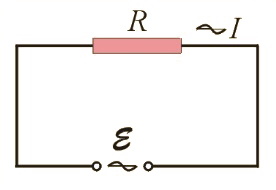
W obwodzie prądu przemiennego, podobnie jak w obwodzie prądu stałego, obowiązują prawa Kirchhoffa (rozdz. 2.8. Prawa Kirchhoffa). Zatem w dowolnej chwili napięcie na oporze jest równe SEM, tzn. lub:
Natężenie prądu zmienia się zatem według zależności:
Widzimy, że amplituda natężenia prądu wynosi:
Zatem wzór (6.5) możemy zapisać w postaci:
Z powyższych wzorów wynika, że w obwodzie z oporem czynnym (zwykły opór nazywamy oporem czynnym, dla odróżnienia od oporów pozornych: pojemnościowego i indukcyjnego, o których powiemy kilka słów pod koniec tego rozdziału, choć wybiega to poza podstawę programową) pod wpływem sinusoidalnej SEM zachodzą drgania harmoniczne natężenia prądu o tej samej częstości i fazie co SEM. Przedstawiono je na wykresie (il. 6.4).
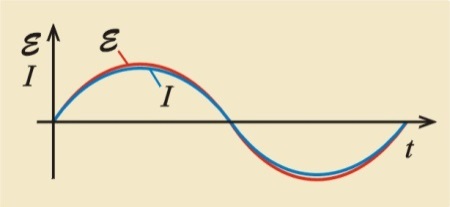
Natężenie skuteczne i napięcie skuteczne
Podobnie jak w przypadku prądu stałego, w obwodzie z oporem czynnym przy przepływie prądu przemiennego wydziela się ciepło Joule'a. Chwilowa moc jest iloczynem oporu i kwadratu chwilowego natężenia prądu:
Jak widać, maksymalna wartość mocy wynosi:
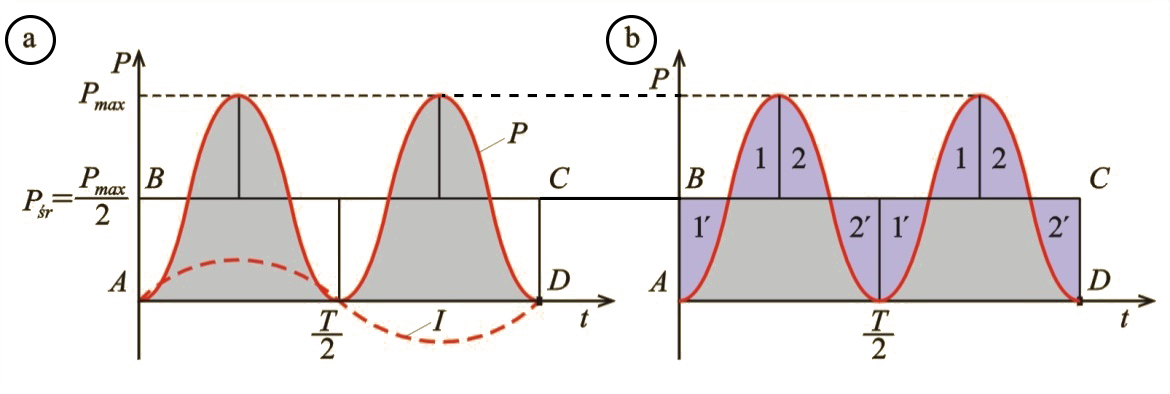
Wykres tej zależności, wraz z wykresem zależności natężenia prądu od czasu (linia przerywana), jest przedstawiony na il. 6.5. Widzimy na nim, że moc zmienia się bardzo szybko (z częstością dwa razy większą niż częstość prądu). Zwykle nie interesuje nas chwilowa wartość mocy liczona w ułamku sekundy, ale jej średnia wartość liczona w dłuższych okresach czasu. Na przykład, jeśli zasilamy prądem przemiennym grzejnik elektryczny, żarówkę lub silnik elektryczny odkurzacza, to ważna jest dla nas średnia moc prądu w tych urządzeniach.
Jak obliczyć średnią moc prądu przemiennego? Wiemy, że moc chwilowa to stosunek pracy do czasu liczony w bardzo krótkich odcinkach czasu: , natomiast moc średnią wyraża taki sam wzór, ale stosunek liczymy w dłuższych odcinkach czasu. Zmiany mocy powtarzają się okresowo, więc średnia moc w czasie równym całkowitej wielokrotności okresu jest równa średniej mocy w jednym okresie. Z kolei dla dowolnie długiego moc średnia jest tym bardziej zbliżona do średniej mocy przypadającej na jeden okres, im dłuższy jest wobec . Przyjmiemy więc, że , gdzie oznacza pracę wykonaną w czasie jednego okresu .
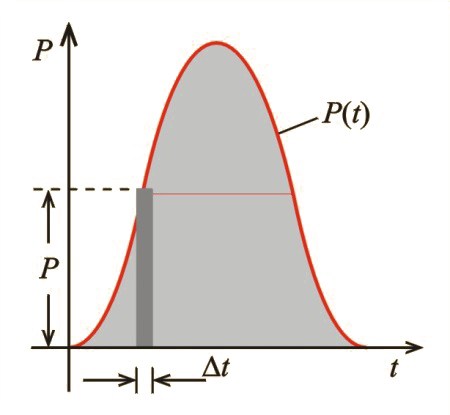
Praca ta to pole powierzchni pod krzywą chwilowej mocy (na il. 6.6 wyróżnione szarym kolorem). Elementarna praca wynosi , co odpowiada polu powierzchni wąskiego paska, wyróżnionego kolorem ciemnoszarym. Suma wszystkich takich pasków to cała praca i w przybliżeniu cała powierzchnia pod krzywą. Bezpośrednie wyznaczenie pola tej powierzchni, równego , wymaga zastosowania rachunku całkowego. Musimy więc zastosować inne metody, wykorzystujące właściwości funkcji trygonometrycznych, by uzasadnić ten wynik.
Jak widać na il. 6.5b, pole tej powierzchni jest równe polu powierzchni prostokąta , którego podstawa jest równa okresowi, a wysokość – połowie maksymalnej wartości mocy. Wynika to z właściwości funkcji , polegającej na tym, że pola i oraz i są parami sobie równe.
Ostatecznym argumentem jest wykorzystanie pomocniczej funkcji , pokazanej na il. 6.7 (linia zielona). Ma ona tę własność, że suma jej i funkcji jest stała i równa – ze względu na tzw. jedynkę trygonometryczną: . Funkcje te przybierają jednakowe wartości, równe , dla argumentów równych i dalej co . Przebiegi tych funkcji są więc swoimi odbiciami względem linii . To zaś oznacza, że pola (odpowiednio ) są równe polom i (odpowiednio i ).
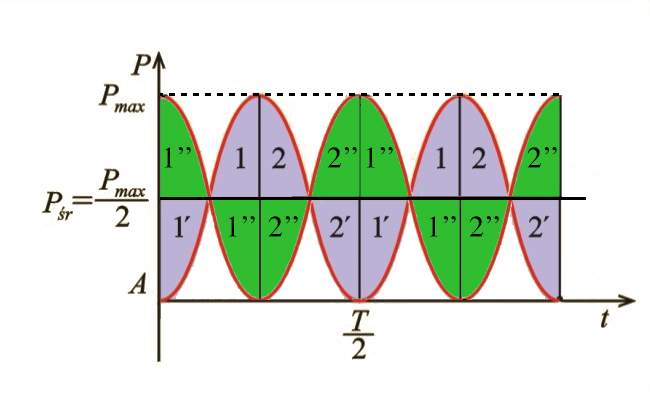
Na tej podstawie stwierdzamy, że:
Zatem
Wartość natężenia , jakie powinien mieć prąd stały, aby jego moc była równa średniej mocy prądu przemiennego, nazywa się natężeniem skutecznym. Porównując wzór na moc tego prądu z wyrażeniem (6.11), otrzymujemy:
a stąd
Widzimy więc, że prąd przemienny o amplitudzie natężenia w swoim działaniu cieplnym lub mechanicznym jest równoważny prądowi stałemu o natężeniu równym . Podobnie definiujemy SEM skuteczną i napięcie skuteczne:
Wzór na moc prądu przemiennego będzie taki sam jak wzór na moc prądu stałego (2.21), bowiem:
Zwykle, jeżeli jest mowa o napięciu lub natężeniu prądu przemiennego, to ma się na myśli właśnie napięcie skuteczne lub natężenie skuteczne.
Zwróćmy uwagę na to, że wzór (6.15) dotyczy mocy prądu przemiennego wydzielonej na oporze w obwodzie, w którym nie są obecne tzw. elementy bierne: cewka i kondensator.
Przykład 1
Zwykle mówi się, że w domowej sieci prądu przemiennego napięcie wynosi 230 V. Co to oznacza? Jakie może być maksymalne napięcie na odbiornikach elektrycznych podłączonych do tej sieci?
Rozwiązanie: Mówiąc o napięciu, mamy tu na myśli przemienną siłę elektromotoryczną. Wartość 230 V odnosi się do SEM skutecznej, zatem:
,więc .
Widzimy, że przy czerpaniu prądu z sieci maksymalne napięcie na odbiorniku elektrycznym wynosi .
Elementy bierne w obwodzie prądu przemiennego
Opornik w obwodzie z prądem przemiennym jest elementem czynnym. Można wymienić dwie role, jakie spełnia on w obwodzie: wraz z amplitudą SEM opór określa amplitudę (lub wartość skuteczną) natężenia prądu (wzór (6.6)) oraz powoduje zamianę energii elektrycznej w obwodzie na energię wewnętrzną lub jej przetwarzanie na inną formę (np. mechaniczną lub świetlną).
W obwód prądu przemiennego można też włączyć dwa rodzaje elementów biernych: kondensator o pojemności (rozdz. 1.7. Pojemność elektryczna) oraz cewkę indukcyjną o współczynniku samoindukcji (rozdz. 4.4. Samoindukcja). Uzyskuje się w ten sposób tzw. obwód RLC. Elementy bierne spełniają w takim obwodzie następujące role.
A. Wraz z amplitudą SEM oraz elementami czynnymi (opornikami) współokreślają amplitudę (lub wartość skuteczną) natężenia prądu. Wprowadzają też dodatkową zależność tej amplitudy od częstotliwości SEM. Elementom biernym przypisujemy zawadę – odpowiednik oporu elektrycznego.
B. Elementy bierne nie przetwarzają energii elektrycznej w inne formy energii. Zapewniają naprzemienne gromadzenie i oddawanie energii elektrycznej. Kondensator gromadzi ją w postaci energii pola elektrycznego, która ma charakter energii potencjalnej, zaś cewka – w postaci energii pola magnetycznego, która jest energią typu kinetycznego.
C. Obecność w obwodzie elementów lub powoduje powstanie przesunięcia fazowego pomiędzy przebiegiem natężenia prądu a przebiegiem napięcia. Takiego przesunięcia nie wywołuje opornik – patrz il. 6.6. Pojawienie się przesunięcia fazowego obniża średnią moc wydzielaną w obwodzie.
D. Cewka i kondensator połączone szeregowo powodują wyróżnianie przez obwód określonej częstotliwości, zależnej od i . Zasilanie obwodu napięciem o tej właśnie częstotliwości wywołuje efekt zbliżony do rezonansu w mechanicznym układzie drgającym (rozdz. 5.5. Drgania wymuszone. Rezonans). Obwód RLC nazywany jest obwodem rezonansowym. Taki obwód, nawet bez obecności sinusoidalnej siły elektromotorycznej SEM, ale jednorazowo zasilony energią (np. przez naładowanie kondensatora) może sam stać się źródłem prądu zmiennego o tej częstotliwości (może stać się obwodem drgającym).
Pełna analiza obwodów RLC i ich właściwości jest niełatwa, ale jest ciekawa i pouczająca. Przedstawimy w ogromnym skrócie podstawowe właściwości tych obwodów, bez wyprowadzeń, jedynie dla przypadku szeregowego połączenia elementów , i . Warto się jednak zapoznać choćby z tak pobieżnym opisem, gdyż obwody te są podstawą wielu zjawisk spotykanych i wykorzystywanych w elektrotechnice, radiotechnice i elektronice.
1. Elementy i schemat
Niech obwód będzie zasilany przez źródło napięcia sinusoidalnie zmiennego o amplitudzie i częstości (rozdz. 6.1. Prądnica prądu przemiennego). Zależność dana jest równaniem:
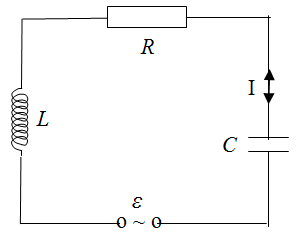
W obwód ten włączono szeregowo opornik , kondensator o pojemności oraz cewkę indukcyjną (zwojnicę) o współczynniku samoindukcji . Schemat uzyskanego w ten sposób obwodu RLC pokazano na il. 6.8.
2. Natężenie prądu
W obwodzie RLC płynie prąd sinusoidalnie zmienny w czasie, o natężeniu danym równaniem:
gdzie:
– amplituda płynącego prądu,
– częstość zmian prądu (równa zawsze częstości zmian napięcia),
– przesunięcie fazowe pomiędzy prądem a napięciem, świadczące o tym, że przebieg zmian tych wielkości nie jest synchroniczny. Brak synchronizacji prądu z napięciem wynika właśnie z obecności w obwodzie elementów biernych i .
3. Zawada elementów biernych; zawada wypadkowa
Odpowiednikiem oporu elektrycznego jest cecha elementu biernego zwana jego zawadą i oznaczana symbolami (zawada pojemnościowa) oraz (zawada indukcyjna). Zawada wyrażana jest, podobnie jak opór, w omach. Podstawowa różnica między zawadą a oporem polega na tym, że zawada zależy nie tylko od właściwości elementu (jego pojemności lub indukcyjności) ale także od częstości zmian przyłożonego napięcia. Zawada pojemnościowa maleje odwrotnie proporcjonalnie do rosnącej częstości, a zawada indukcyjna rośnie proporcjonalnie do częstości:
Zwróćmy tu uwagę na ciekawy skutek odwrotnej zależności każdej z zawad od . W przypadku małych wartości (mówimy wtedy o prądach powoli zmiennych lub wolnozmiennych) zawada staje się niewielka, za to zawada rośnie nieograniczenie, gdy dąży do zera. Oznacza to, że prąd powoli zmienny napotka na poważną „zawadę” pojemnościową w obwodzie. Z kolei przy bardzo dużych wartościach (mówimy wtedy o prądach szybkozmiennych) zawada staje się niewielka, za to zawada nieograniczenie rośnie wraz ze wzrostem . Oznacza to, że prąd szybkozmienny także napotka na poważną „zawadę” w obwodzie, choć tym razem będzie to zawada indukcyjna.
Nieco nietypowe jest wyrażenie podające wypadkową zawadę elementów połączonych szeregowo – nie jest ona zwykłą sumą zawad elementów składowych, lecz wyraża się wzorem:
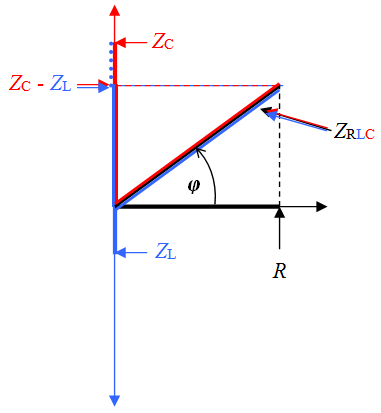
Często stosowaną graficzną interpretację wzoru (6.19) pokazano na il. 6.9. Na poziomej osi odkładamy wartość oporu czynnego . Na pionowej osi odkładamy wartości zawad elementów biernych: pojemnościową – w górę, indukcyjną – w dół. Odejmujemy graficznie od , otrzymując na pionowej osi odcinek o długości – odpowiada on wypadkowej zawadzie elementów biernych. Odcinki oraz wyznaczają prostokąt, którego przekątna ma długość . Kąt między tą przekątną a osią jest kątem przesunięcia fazowego pomiędzy napięciem a natężeniem prądu. O przesunięciu fazowym będziemy mówić w punkcie 5.
4. Prawo Ohma dla amplitudy natężenia prądu
Za pomocą wyrażenia (6.19) można zapisać związek amplitudy natężenia prądu z amplitudą napięcia . Ma on postać prawa Ohma:
Taki sam związek obowiązuje dla skutecznych wartości napięcia i natężenia :
5. Przesunięcie fazowe
Przesunięcie fazowe pomiędzy przebiegiem napięcia (czysto sinusoidalnym) a przebiegiem natężenia prądu wyraża się najprościej przez funkcje trygonometryczne:
lub w sposób nieco bardziej ogólny:
Ostatni wzór pokazuje, że przesunięcie fazowe może być dodatnie (dla obwodów „pojemnościowych”, w których ) lub ujemne (dla obwodów „indukcyjnych”, w których ). Wartości są ograniczone do przedziału , czyli od do .
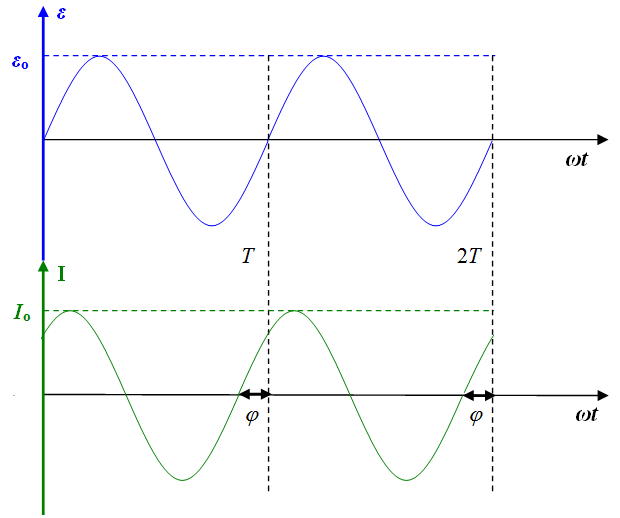
Na wykresie (il. 6.10) pokazano sinusoidalny przebieg oraz przesunięty w fazie o przebieg w obwodzie „pojemnościowym”.
6. Przemiany energii w obwodzie RLC; wydzielana moc średnia
Zależność mocy od czasu dana jest iloczynem chwilowego napięcia i chwilowego natężenia prądu:
Iloczyn oznaczono tu symbolem i wykorzystano tożsamość trygonometryczną:
Wykres funkcji wraz z przebiegami oraz pokazano na il. 6.11. Wartości mocy maksymalna i minimalna spełniają warunek: . Funkcja jest funkcją trygonometryczną o okresie dwukrotnie krótszym od i o amplitudzie równej ; jest ona przesunięta wzdłuż osi o wartość . Ta ostatnia cecha jest istotna, gdyż to ona determinuje średnią wartość mocy w ciągu jednego okresu:
Ostatecznie otrzymujemy:
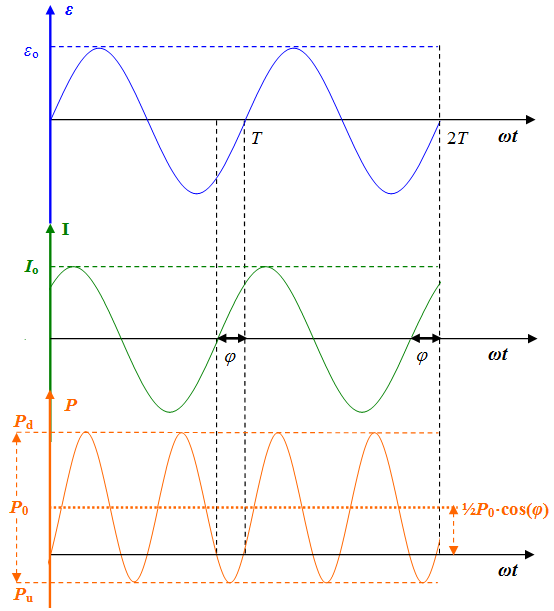
Skąd się biorą i co oznaczają ujemne fragmenty zależności ? W każdej chwili na oporze czynnym następuje przetwarzanie energii elektrycznej w energię wewnętrzną, świetlną, mechaniczną itp. To przetwarzanie jest nieodwracalne. Związaną z tym moc traktujemy jako dodatnią – taką interpretację przyjęliśmy na wykresach na il. 6.7. Równolegle zachodzą procesy gromadzenia bądź oddawania (zależy to od rozpatrywanej chwili) energii elektrycznej przez elementy bierne. Objawem oddawania energii elektrycznej przez element bierny do obwodu jest właśnie przyjmowanie przez chwilową moc wartości ujemnych.
7. Stan rezonansowy
Specyficzną cechą obwodu RLC jest możliwość uzyskania w nim stanu rezonansowego. Polega to na takim doborze parametrów , i , by zminimalizować zawadę . Jeśli spojrzymy uważnie na wzór (6.19), to zauważymy, że gdy , to . Każda inna relacja pomiędzy i prowadzi do wzrostu . Równość oznacza zaś, po uwzględnieniu wzoru (6.18), że:
Przy takim doborze parametrów nie tylko zawada całkowita obwodu jest minimalna, ale natężenie prądu w nim płynące ma maksymalną amplitudę (wzór (6.20)), zaś przesunięcie fazowe (wzory (6.21) i (6.22)). To wszystko powoduje, że w stanie rezonansowym wydziela się w obwodzie maksymalna moc (wzór (6.24)). Zależność amplitudy natężenia prądu od częstości pokazano na il. 6.12. Krzywa ta, o charakterystycznym „dzwonowym” kształcie, nazywa się krzywą rezonansową.
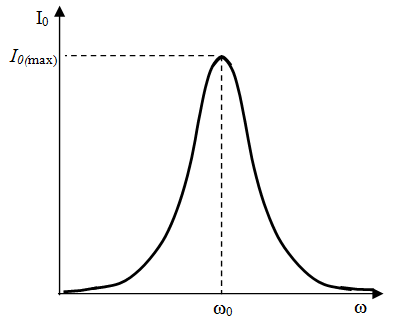
Obwód RLC „wyróżnia” częstość daną wzorem (6.25) – jest on szczególnie podatny na zasilanie napięciem zmiennym z tą częstością. Częstość tę nazywa się częstością rezonansową obwodu lub jego częstością własną; jest ona oznaczana symbolem :
Szczególnie ciekawym aspektem krzywej rezonansowej jest osiąganie przez amplitudę natężenia prądu maksymalnej wartości przy . Ta właściwość obwodu jest wykorzystywana np. w odbiornikach fal radiowych do dostrajania odbiornika do żądanej stacji. Poprzez regulację pojemności kondensatora i/lub współczynnika samoindukcji cewki w obwodzie połączonym z anteną odbiornika, nastawia się częstość własną tego obwodu. W ten sposób wyklucza się praktycznie możliwość wzbudzania w antenie prądów o częstotliwości innej niż wybrana. Unika się w ten sposób zakłóceń w odbiorze tej stacji.
8. Obwód drgający
Obwód RLC nie wymaga ciągłego zasilania napięciem zmiennym – takie zasilanie jest odpowiednikiem wymuszania drgań mechanicznych, opisanego w rozdz. 5.5. Drgania wymuszone. Rezonans. Wiemy jednak, że drgania mechaniczne można pobudzić przez jednorazowe dostarczenie energii (potencjalnej lub kinetycznej). Podobnie, w obwodzie RLC można wzbudzić przepływ prądu zmiennego poprzez naładowanie kondensatora lub przepuszczenia prądu przez cewkę. Obwód realizujący tę pierwszą możliwość przedstawiono na il. 6.13.
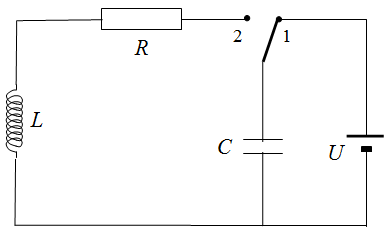
Po naładowaniu kondensatora stałym napięciem (przełącznik w poz. 1) następuje jego rozładowanie przez cewkę i opornik (przełącznik w poz. 2). Energia pola elektrycznego zgromadzona w kondensatorze częściowo rozprasza się na oporniku, ale częściowo zamienia się w energię pola magnetycznego w cewce. W dalszym ciągu procesu ta ostatnia także częściowo się rozprasza, ale częściowo zamienia się w energię pola elektrycznego w kondensatorze. Jeśli wartość jest odpowiednio mała, w obwodzie płynie prąd zmienny o zanikającej w czasie amplitudzie:
gdzie:
– malejąca w czasie amplituda płynącego prądu,
– częstość zmian prądu, równa w przybliżeniu (wzór (6.26)); przybliżenie to jest tym lepsze, im opór jest mniejszy.
Taki obwód może być źródłem fali elektromagnetycznej, jeśli konstrukcja kondensatora lub cewki umożliwia rozchodzenia się pola, odpowiednio – elektrycznego lub magnetycznego, w przestrzeń poza obwód.
Pytania i problemy
- Przedstaw graficznie pracę prądu przemiennego i tym sposobem oblicz średnią pracę wykonaną w ciągu jednego okresu.
- Jeżeli mówimy, że źródło napięcia przemiennego domowej sieci ma napięcie 230 V, to co to oznacza? Czy to, że chwilowa wartość napięcia, np. na końcach włókna żarówki, nie może przekroczyć 230 V? Odpowiedź uzasadnij.
- Zdefiniuj napięcie i natężenie skuteczne. Przedstaw związek między maksymalną i skuteczną wartością napięcia i natężenia prądu przemiennego.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
