Do opisu zjawisk powstawania obrazów w różnych instrumentach optycznych wykorzystuje się zasady geometrii. Światło ma jednak charakter falowy, dlatego pełny opis powstawania obrazów, uwzględniający wszystkie występujące tu zjawiska, powinien się opierać na prawach ruchu fal, czyli na prawach optyki falowej. Przykład takiego opisu powstawania obrazu w soczewce, według teorii Abbego, podaliśmy w Dodatku do tego rozdziału. Stosowanie tej teorii do wszystkich przypadków byłoby zbyt skomplikowane. Dlatego chętnie korzystamy z praw optyki geometrycznej, dającej wprawdzie opis przybliżony, ale za to dużo prostszy. Zanim poznano falową naturę światła, do rozwiązywania problemów związanych z powstawaniem obrazów w soczewkach i zwierciadłach uczeni z powodzeniem stosowali metody geometryczne.

Optyka geometryczna sprowadza się właściwie do zastosowania trzech praw: prawa prostoliniowego rozchodzenia się światła (w ośrodkach jednorodnych), prawa odbicia światła i prawa załamania światła. Dwa ostatnie prawa wynikają z optyki falowej i mogą być stosowane bez ograniczeń. Natomiast prawo prostoliniowego rozchodzenia się światła ma swoje ograniczenia. Wiemy, że w różnych instrumentach optycznych światło przechodzi przez różne otwory, tzw. diafragmy. Przy przechodzeniu światła przez bardzo małe otwory następuje zauważalne ugięcie się fali światła i to ogranicza zakres stosowania optyki geometrycznej. Podstawowymi pojęciami optyki geometrycznej są wiązka świetlna i promień światła. Wiązka świetlna ma określone rozmiary geometryczne przekroju poprzecznego kanału (najczęściej cylindrycznego lub stożkowego), wewnątrz którego rozchodzi się światło, natomiast promień światła to oś geometryczna wiązki świetlnej. Charakteryzuje on kierunek rozchodzenia się energii światła.

Każdy z nas spotkał się z pryzmatem, gdyż jest to powszechnie stosowany przyrząd optyczny, który ma dużo różnorodnych zastosowań. W rozdziale 8.3. Dyspersja światła poznaliśmy jego zdolność do rozszczepiania światła białego na barwne wiązki monochromatyczne. Obecnie skupimy się nad jego zdolnością do zmiany kierunku biegu promieni świetlnych.

Pryzmat to graniastosłup, najczęściej o podstawie trójkątnej, wykonany ze szkła lub innego przezroczystego materiału. Kąt wierzchołkowy $\phi$ (il. 8.45) nazywa się kątem łamiącym pryzmatu. Aby zbadać własności załamania światła w pryzmacie, przeprowadzimy następujące doświadczenie.

Doświadczenie pokazowe

Na urządzeniu do pomiaru kątów padania i załamania wiązek światła (il. 8.44) ustawiamy pryzmat o kącie łamiącym około $60°$. Na jedną ściankę pryzmatu kierujemy wiązkę światła monochromatycznego w pobliże kąta łamiącego (tak, aby część wiązki załamywała się w pryzmacie, a część przechodziła obok) pod kątem padania równym prawie $90°$. Obracamy pryzmat dookoła osi przechodzącej przez punkt padania promienia na ściankę pryzmatu, zmniejszając stopniowo kąt padania.

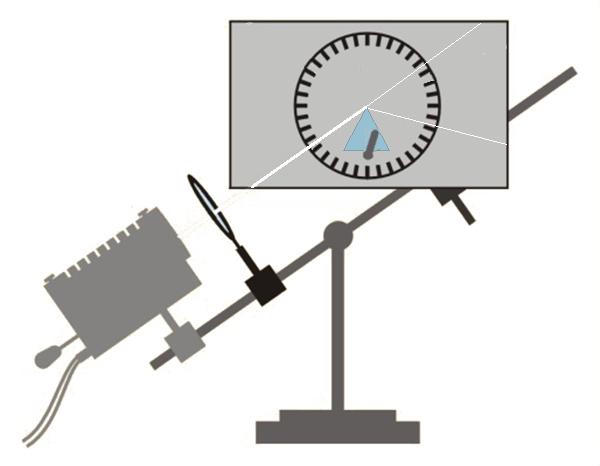
Obserwujemy kąt $\epsilon$ odchylenia promienia od pierwotnego kierunku, czyli kąt między promieniem światła wychodzącym z pryzmatu a przedłużeniem promienia padającego. Zauważamy, że w miarę zmniejszania się kąta padania $\alpha$ kąt odchylenia $\epsilon$ początkowo maleje, a następnie, począwszy od pewnej wartości kąta padania, zaczyna rosnąć. Zatem istnieje taka wartość kąta padania $\alpha$, przy której kąt odchylenia jest najmniejszy (il. 8.46). Dokładniejsza obserwacja wskazuje, że kąt odchylenia przybiera minimalną wartość, gdy kąt padania $\alpha$ jest równy kątowi $\delta$ wyjścia z pryzmatu.

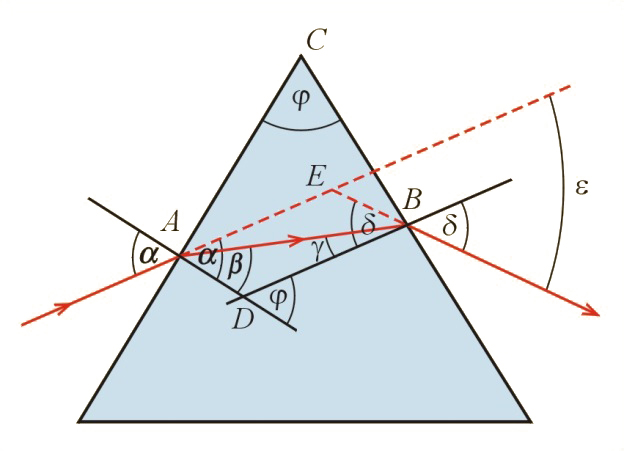
Rozważymy teraz, od czego zależy kąt odchylenia promienia w pryzmacie $\epsilon$. Odpowiednie kąty są zaznaczone na il. 8.45. Kąt $\epsilon$ jest kątem zewnętrznym w trójkącie $AEB$, więc jest równy sumie kątów przeciwległych. Zatem:

$\epsilon =\left(\alpha -\beta \right)+\left(\delta -\gamma \right)$ lub $\epsilon =\left(\alpha +\delta \right)-\left(\beta +\gamma \right)$.

Ponieważ $\beta +\gamma =\phi$,

Wzór ten nie pozwala jednak rozstrzygnąć, jak zmienia się $\epsilon$, gdy rośnie kąt padania $\alpha$, gdyż wtedy maleje kąt $\delta$. Jednakże wzór ten daje się uprościć w przypadku, gdy kąt łamiący pryzmatu jest mały i kąt padania jest też mały. Wtedy także kąty $\beta$, $\gamma$ i $\delta$ będą małe i zgodnie z tym, co pamiętamy z trygonometrii, odpowiednie sinusy kątów dadzą się w przybliżeniu wyrazić przez te kąty (wyrażone w radianach). Ponadto na podstawie wzoru (8.3) wiemy, że współczynnik załamania $n=\frac{sin\alpha }{sin\beta }$. Zatem:

$n\approx \frac{\alpha }{\beta }$ i $n\approx \frac{\delta }{\gamma }$, stąd $\alpha =n\beta$ i $\delta =n\gamma$.

Po podstawieniu do wzoru (8.40) otrzymamy:

Jeszcze raz wykorzystamy równanie $\phi =\beta +\gamma$. Mamy więc:

Jest to wzór przybliżony, który dla małych kątów łamiących pozwala przewidzieć kąt odchylenia promienia w pryzmacie, jeżeli jest dany współczynnik załamania szkła lub innego materiału, z którego wykonany jest pryzmat.

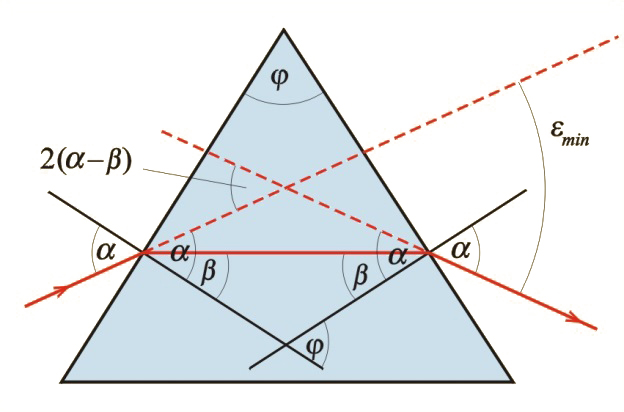
Znając kąt łamiący pryzmatu $\phi$ i mierząc ${\epsilon }_{min}$, można wyznaczyć współczynnik załamania pryzmatu $n$. Do tego celu może służyć wzór:

Wzór ten łatwo wyprowadzimy, pamiętając, że kąt odchylenia przybiera minimalną wartość ${\epsilon }_{min}$, gdy kąt padania $\alpha$ jest równy kątowi wyjścia $\delta$ z pryzmatu, tzn. $\alpha =\delta$, jak to jest na il. 8.46. Wiadomo, że:

a na rysunku widzimy, że $\phi =2\beta$, tzn. że $\beta =\frac{\phi }{2}$. Ponadto ${\epsilon }_{min}=2\left(\alpha -\beta \right)=2\alpha -2\beta$, więc ${\epsilon }_{min}=2\alpha -\phi$ lub $\alpha =\frac{\phi +{\epsilon }_{min}}{2}$.

Po podstawieniu do wzoru (8.44) wyrażenia na $\alpha$ i $\beta$ otrzymujemy wzór (8.43).

EXE Załamanie światła, Pryzmat

Pytania i problemy

1. Przedstaw na rysunku przejście światła monochromatycznego przez pryzmat. Zaznacz kąt odchylenia promienia w pryzmacie i kąt łamiący pryzmatu. Podaj definicję obu kątów.
2. Udowodnij, że kąt odchylenia w pryzmacie można przedstawić za pomocą równania $\epsilon =\left(n-1\right)\phi$. Podaj warunki, w jakich ten wzór jest stosowalny.
3. Kiedy kąt odchylenia wiązki światła w pryzmacie przybiera wartość minimalną ${\epsilon }_{min}$? Wyprowadź równanie przedstawiające związek między współczynnikiem załamania pryzmatu, kątem łamiącym pryzmatu i minimalną wartością kąta odchylenia promienia.