Koherencja światła

Nieobserwowanie interferencji przy oświetleniu powierzchni za pomocą dwóch lub kilku lamp ma przyczynę w tym, że fale świetlne pochodzące z tych źródeł nie są zgodne ze sobą – mówimy, że nie są spójne lub koherentne. W celu otrzymania stabilnego obrazu interferencyjnego, fale muszą być spójne. Falami koherentnymi (lub spójnymi) nazywamy takie fale, które mają jednakową długość oraz stałą w czasie różnicę faz we wszystkich miejscach obszaru, w którym się nakładają (owa różnica faz jest na ogół różna dla różnych punktów).

A jakie fale świetlne wysyła zwykła żarówka? Promieniuje światło w ten sposób, że poszczególne atomy włókna żarówki wypromieniowują ciągi falowe (długości kilku metrów) przypadkowo – niezależnie jeden od drugiego. Wyświecanie pojedynczego ciągu falowego przez atom trwa około ${10}^{-8}\text{s}$. Zatem, jeżeli spotkają się dwie wiązki z różnych źródeł, różnica faz poszczególnych ciągów falowych obu wiązek będzie się zmieniać w sposób przypadkowy. Powstanie, owszem, jakiś obraz interferencyjny, ale po czasie rzędu owych ${10}^{-8}\text{s}$ zostanie on zastąpiony zupełnie innym obrazem, bez związku z poprzednim. Nie ma więc warunków do wystąpienia interferencji, która mogłaby być zarejestrowana przez większość przyrządów czy przez nasze oko.

Jednakże możliwe jest zaobserwowanie interferencji światła pochodzącego ze zwykłych źródeł. Co ciekawsze, interferencja światła była od dawna obserwowana, ale ludzie nie zdawali sobie sprawy z tego. Na pewno wiele razy widziałeś efekt interferencji światła, bawiąc się w dzieciństwie bańkami mydlanymi, które – szczególnie w świetle słonecznym – wspaniale się zabarwiają tęczowymi kolorami. Obserwując światło odbite od kałuży, na której są plamy oleju lub nafty, widzimy, że mieni się ono różnymi kolorami – jest to efekt interferencji światła.

Bezdyfrakcyjna interferencja światła

Jak wytłumaczyć zabarwienie cienkich błonek oraz zmiany ich kolorów w zależności od kąta widzenia? Na il. 8.21 przedstawiono promień $1$ padający na powierzchnię cienkiej błonki, który częściowo odbija się w postaci promienia $1\text{'}$, a częściowo przechodzi jako promień $1\text{'}\text{'}$ do ośrodka błonki, załamując się, i po odbiciu od przeciwległej wewnętrznej powierzchni wychodzi z tego ośrodka, ponownie się załamując, po czym obie części promienia poruszają się równolegle i interferują ze sobą. Jeżeli promień $1\text{'}\text{'}$, który ma do przebycia dłuższą drogę, spóźnia się w stosunku do promienia $1\text{'}$ o całkowitą wielokrotność długości fali, to następuje wzmocnienie fali; jeżeli natomiast spóźnia się o całkowitą, nieparzystą wielokrotność połowy długości fali, to nastąpi osłabienie fali wypadkowej. Rezultat zależy od kąta padania promienia, grubości i współczynnika załamania błonki oraz od długości fali.

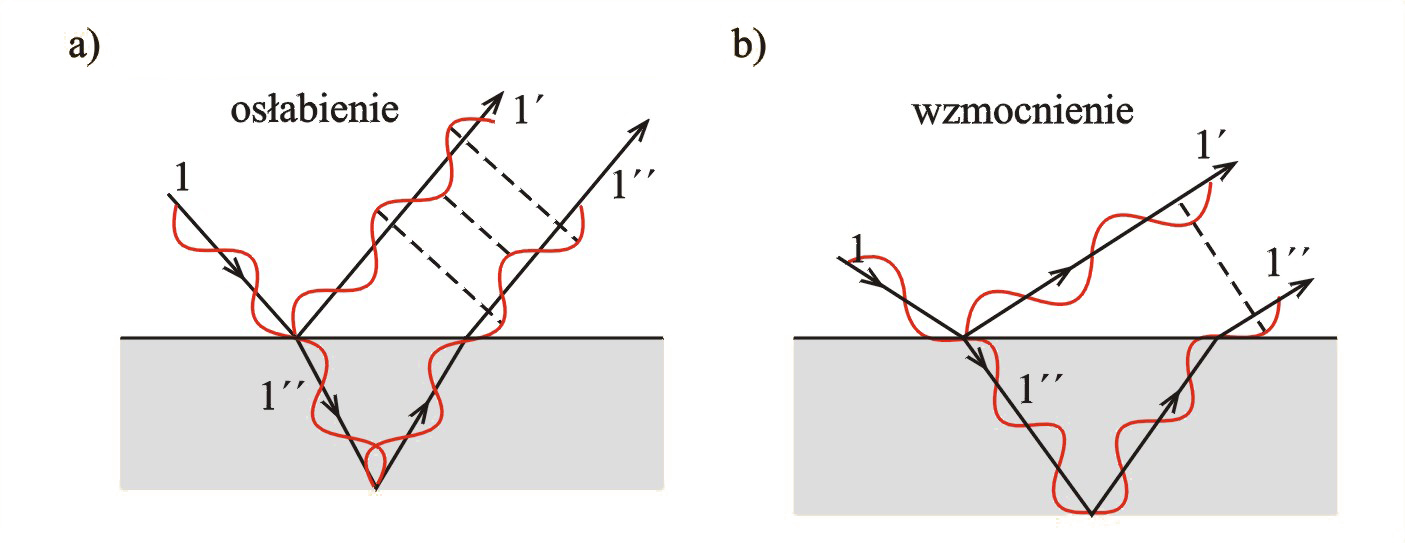
W tym przypadku, mimo że światło pochodzi ze zwykłego źródła, obie wiązki – $1\text{'}$ i $1\text{'}\text{'}$ – są koherentne, ponieważ każdy ciąg falowy ulega rozszczepieniu na dwa ciągi, które następnie łączą się ze sobą po przebyciu różnych dróg. Dla wszystkich ciągów falowych o jednakowej długości fali przy danym kącie padania występuje taka sama różnica faz między promieniem odbitym od zewnętrznej powierzchni błonki a promieniem odbitym od powierzchni wewnętrznej. Występują więc warunki do stabilnej interferencji. Jeżeli na błonkę pada światło białe, to w danym kierunku wzmocni się (lub wygasi) tylko fala o określonej długości. Barwa światła, którego fala została wzmocniona, dominuje nad pozostałymi i właśnie tę barwę obserwujemy. Natomiast jeśli w widmie światła białego zabraknie fali określonej długości, to światło uzyska barwę dopełniającą. Jeżeli błonka ma różną grubość, to przy oświetleniu światłem białym pojawią się różne barwy.

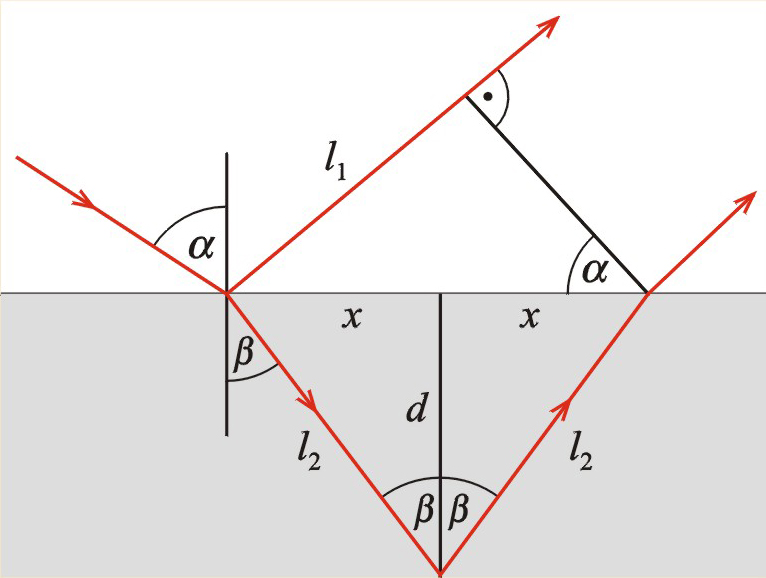
Wyprowadzimy teraz wzory będące warunkami na wzmocnienie i osłabienie fali. Fale $1\text{'}$ i $1\text{'}\text{'}$ będą się wzmacniać, gdy spotkają się w fazach zgodnych, więc gdy różnica długości odcinków $l_1$ i $2l_2$ (il. 8.22) jest całkowitą wielokrotnością długości fal (na razie nie uwzględniliśmy zmiany fazy przy odbiciu fali od zewnętrznej ani wewnętrznej powierzchni błonki). Stąd:

gdzie $m$ jest liczbą całkowitą, ${\lambda }_b$ jest długością fali w błonce, zaś $\lambda$ – długością fali w powietrzu. Zależność między tymi długościami fal otrzymamy ze związku: $n=\frac{c}{v}=\frac{\lambda \nu }{{\lambda }_b\nu }$, więc:

Po uwzględnieniu tego wzoru warunek (8.14) przybierze postać:

Teraz uwzględnimy zmianę fazy przy odbiciu od powierzchni błonki. Z teorii ruchu falowego wiadomo, że przy odbiciu fali od ośrodka gęstszego następuje zmiana fazy na przeciwną (rozdz. 5.12. Fale stojące – przypomnij sobie odbicie fali na sznurze umocowanym do ściany – il. 5.32). W przypadku fali świetlnej ośrodkiem o większej gęstości optycznej jest ośrodek o większym współczynniki załamania. Zatem przy odbiciu promienia od zewnętrznej powierzchni błonki następuje przesunięcie fazy o $\pi$, zaś przy odbiciu od wewnętrznej powierzchni takie przesunięcie fazy nie następuje. Po uwzględnieniu tych rozważań warunek (8.16) przyjmuje postać:

Z il. 8.22 możemy odczytać, że $l_2=\frac{d}{cos\beta }$ oraz $l_1=2xsin\alpha =2dtg\beta sin\alpha =\frac{2dsin\beta sin\alpha }{cos\beta }$. Po uwzględnieniu tych wyrażeń we wzorze (8.17) otrzymamy:

Po podstawieniu $n=\frac{sin\alpha }{sin\beta }$ i po prostych przekształceniach otrzymamy:

Natomiast warunek osłabienia, przy uwzględnieniu zmiany fazy przy odbiciu fali od powierzchni zewnętrznej błonki, otrzymamy z równania podobnego do (8.17):

Po przekształceniach, dla osłabienia fali otrzymamy warunek:

Podsumujmy wyniki naszych rozważań: