8.6. Dyfrakcja i interferencja światła

Wcześniej podkreślaliśmy, że charakterystyczną cechą ruchu falowego jest interferencja. Również i dyfrakcja jest charakterystyczną cechą ruchu falowego. Z dyfrakcją fali zaznajomiliśmy się przy rozpatrywaniu fal na wodzie przechodzących przez szczeliny (patrz rozdz. 5.10. Zasada Huygensa, ugięcie fali). Doświadczenie przekonuje nas, że fala płaska, przechodząc przez mały otwór, ugina się i za otworem rozchodzi się w różnych kierunkach, jak na il. 8.27a. Obraz ugięcia fali objaśniliśmy zasadą Huygensa, która mówi że każdy punkt powierzchni falowej jest źródłem nowej fali kulistej. Taki obraz jak na il. 8.27a otrzymamy wtedy, gdy rozmiary otworu są porównywalne z długością fali, wtedy bowiem możemy przyjąć, że otwór przepuszcza tylko jedną falę kulistą spośród wielu takich fal składających się na czoło fali dochodzącej do przeszkody. Jeżeli będziemy poszerzać otwór w przeszkodzie, to wiele fal kulistych czoła fali dochodzącej do otworu utworzy falę płaską, która przejdzie bez ugięcia, ugięcie zajdzie tylko na krawędziach otworu (il. 8.27b). Ten obraz jest jednak przybliżony, gdyż fale kuliste wychodzące z takiego otworu będą interferować. Skutek takiej interferencji opiszemy na przykładzie fal świetlnych.

Ugięcie fali — Ilustracja 8.27. a) ugięcie fali jest wyraźnie obserwowalne dla małych otworów, przez które przechodzi fala, b) im większy otwór, tym mniejsza część energii fali rozchodzi się na boki

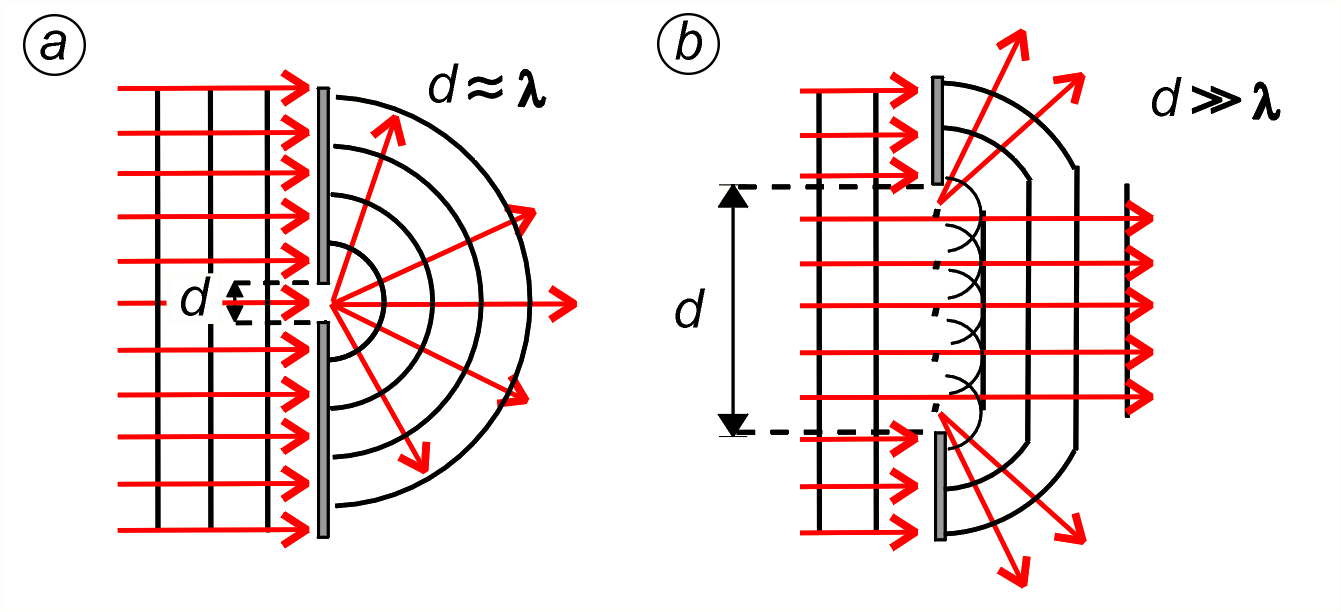
Energia obserwowanego promieniowania w określonym kierunku zależy od tego, ile fal elementarnych składa się na obserwowaną falę (padającą na odbiornik fali). Ze względu na to, że fale świetlne mają bardzo małą długość fali $\lambda$ , przy otworach o rozmiarach rzędu 0,1 mm olbrzymia większość fal elementarnych utworzy falę płaską, a tylko pojedyncze na krawędziach otworu dadzą efekt dyfrakcyjny (patrz il. 8.27b). Porównajmy, ile razy średnica otworu $d=0,1\, mm=10^{-4}\, m$ jest większa od przeciętnej długości fali światła $\lambda=500\, nm=5.10^{-7}\, m$ . Otrzymamy: $d/\lambda=200$ , czyli średnica otworu jest dwieście razy większa od długości fali. Zatem nic dziwnego, że dyfrakcja nawet na tak małym otworze jest bardzo słaba i praktycznie niezauważalna. Dlatego w optyce geometrycznej, gdzie rozpatrujemy bieg światła w różnych przyrządach optycznych, takich jak lupa, luneta, czy mikroskop, możemy przyjąć podstawową zasadę prostoliniowego rozchodzenia się promieni światła.

Zjawisku ugięcia towarzyszy interferencja fal elementarnych zachodząca za otworem.

Doświadczenie pokazowe: Interferencja w ugiętej wiązce światła

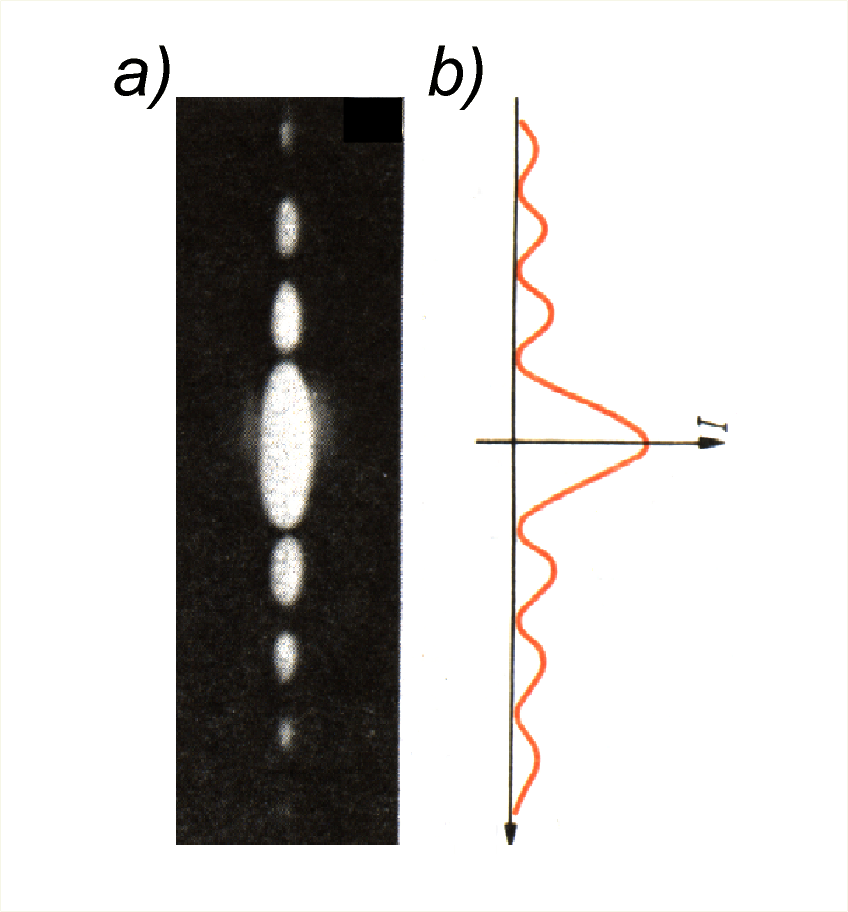
Na drodze wiązki światła z lasera ustawiamy wąską szczelinę o szerokości ok. 0,3 mm, a dalej ekran, jak na il. 8.28. Na ekranie zaobserwujemy obraz dyfrakcyjny szczeliny składający się z jednego silnego wąskiego pasma w środku i wielu coraz słabszych pasm po obu stronach pasma środkowego – il. 8.29a.

Na il. 8.29b przedstawiono zależność natężenia światła od kąta ugięcia.

Ilustracja 8.28. **Układ doświadczalny dla obserwacji dyfrakcji światła na szczelinie**

Zdjęcie obrazu dyfrakcyjnego szczeliny — Ilustracja 8.29. **a) zdjęcie obrazu dyfrakcyjnego szczeliny, b) zależność natężenia światła od kąta ugięcia**

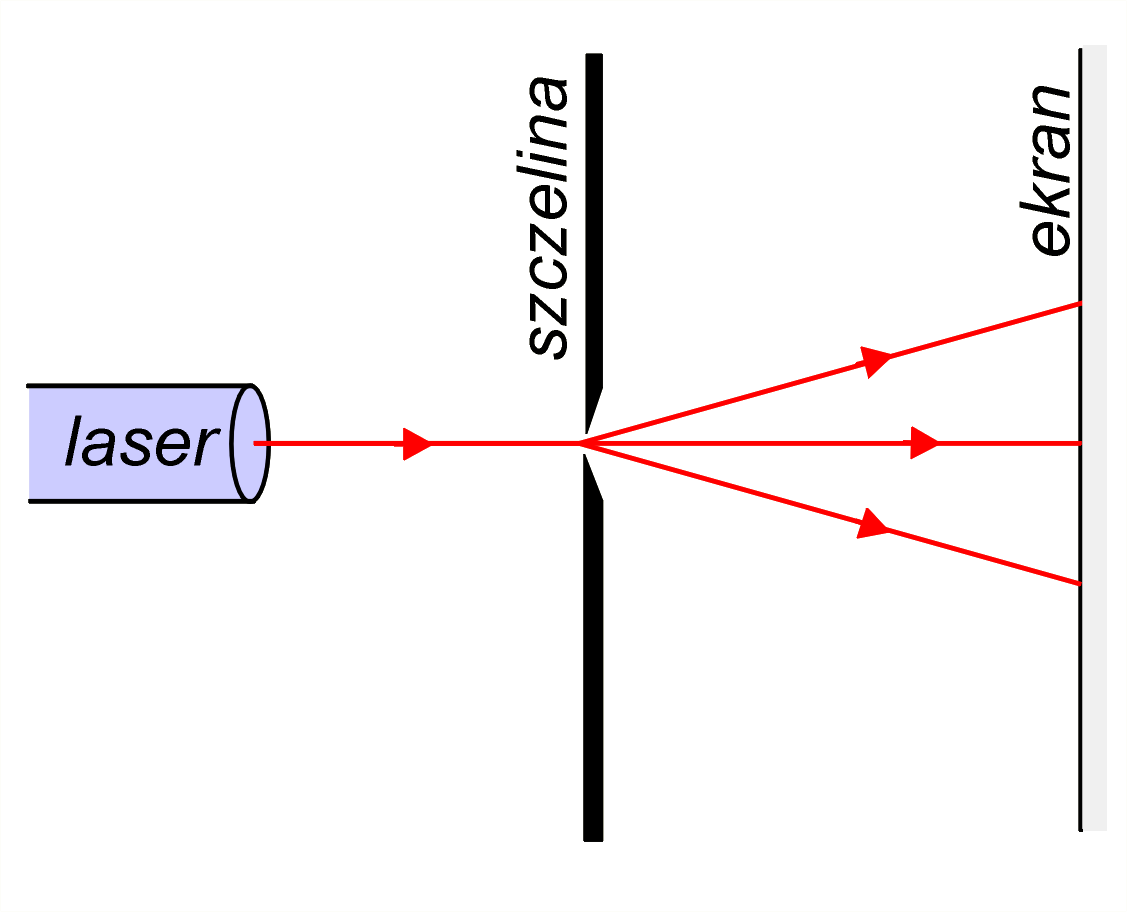
Na il. 8.30 pokazano, jak powstaje obraz dyfrakcyjny szczeliny na ekranie.

Zgodnie z zasadą Huygensa wzmocnienia, naprzemiennie z wygaszaniem fal zachodzą w określonych kierunkach — Ilustracja 8.30. **Zgodnie z zasadą Huygensa, wzmocnienia fal, naprzemiennie z ich wygaszaniem, zachodzą w określonych kierunkach**

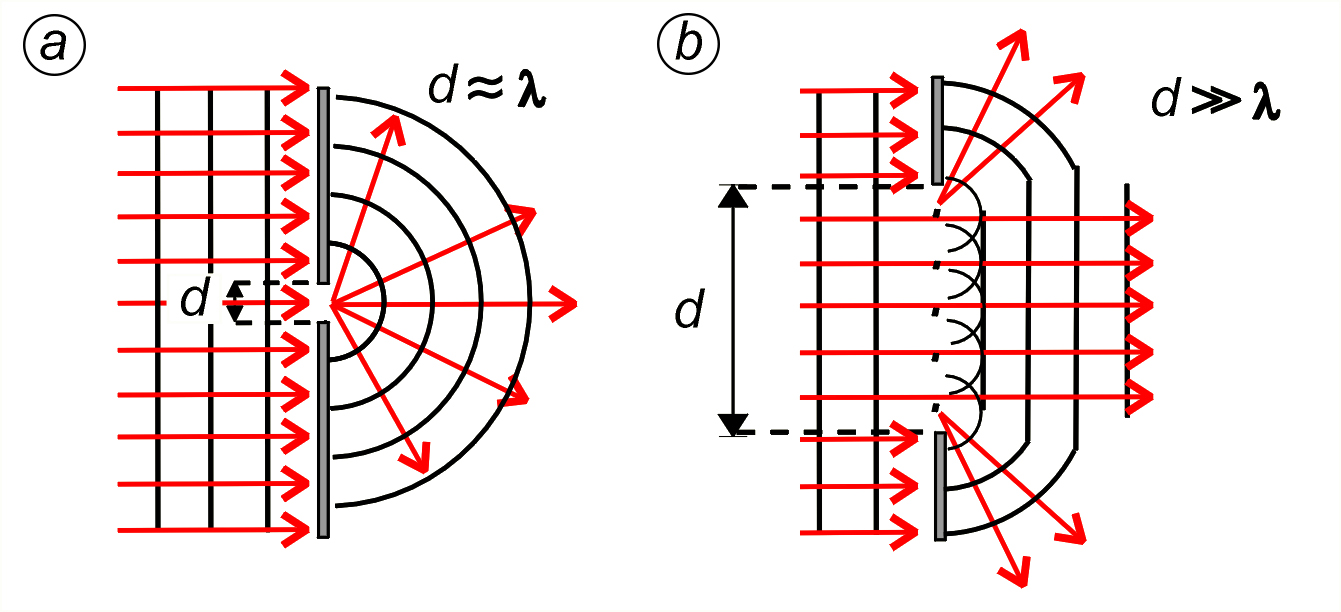
Biorąc pod uwagę zasadę Huygensa, widzimy, że będziemy mieli do czynienia, naprzemiennie, ze wzmocnieniem i wygaszaniem fali. Linie proste ciągłe przedstawiają powierzchnie falowe, linie przerywane czerwone kierunki rozchodzenia się fal wzmocnionych. Im większy kąt ugięcia $\vartheta$ , tym mniej energii przypada na jednostkowy przekrój powierzchni fali.

Bliższe rozważenie dyfrakcji ułatwi nam zrozumienie, na czym polega rewelacyjne odkrycie optyki XX wieku – holografii, o której więcej możesz przeczytać w rozdziale 8.D1. Dodatek: Holografia (temat nadobowiązkowy). Dlatego przyjrzymy się bliżej dyfrakcji fali świetlnej na szczelinie.

Wzór na amplitudę fali ugiętej na szczelinie przedstawia się następująco:

A_{w}=A_{0}\frac{\sinu}{u}

( 8.24 )

gdzie pomocnicza zmienna $u$ zawiera informację o stosunku szerokości szczeliny $d$ do długości fali $\lambda$ oraz o kącie ugięcia $\vartheta$ :

u=\pi\frac{d}{\lambda}\sin\vartheta

zaś $A_{0}$ jest amplitudą fali padającej pod kątem $\vartheta=0$ .

Natężenie fali jest proporcjonalne do kwadratu amplitudy. Zatem natężenie fali w kierunku obserwacji $\vartheta$ wyniesie:

I=I_{0}\frac{\sin^{2}u}{u^{2}}

( 8.25 )

Wykres zależności stosunku natężenia $I$ do natężenia maksymalnego $I_{0}$ fali ugiętej od kąta ugięcia $\vartheta$ według wzoru (8.25) dla szczeliny o szerokości $d=5\lambda$ pokazano na il. 8.31a. Widzimy, że wykres odtwarza przebieg dyfrakcji otrzymany w doświadczeniu. Wzmocnienia i wygaszenia natężenia występują naprzemiennie. Natężenia maksimów kolejnych, coraz wyższych rzędów, szybko maleją po obu stronach głównego maksimum. Już natężenie w maksimum pierwszego rzędu stanowi zaledwie około 5% $I_{0}$ .

Wykres zależności amplitudy fali ugiętej na pojedynczej szczelinie — Ilustracja 8.31. a) wykres zależności natężenia względnego $I/I_{0}$ fali ugiętej na pojedynczej szczelinie od kąta ugięcia $\vartheta$ , b) taki sam wykres dla szczeliny 10-krotnie szerszej

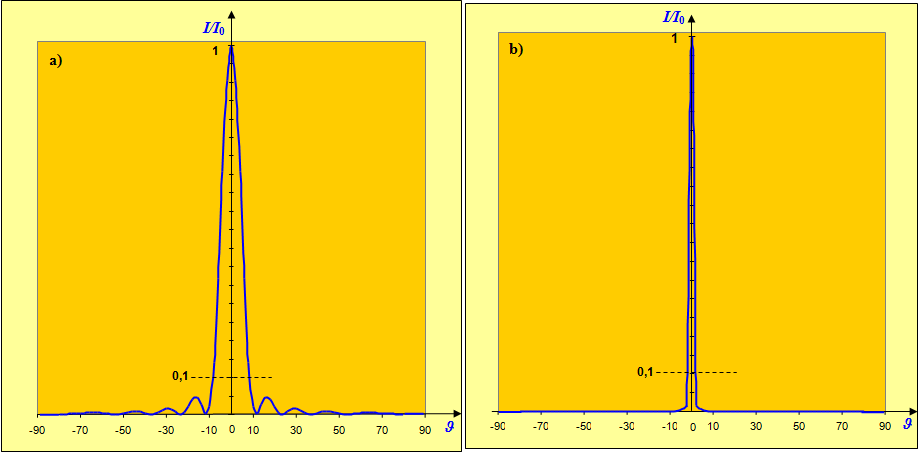
Na il. 8.31b przedstawiono taki sam wykres dla szczeliny o szerokości $d=50\lambda$ . Struktura dyfrakcyjno-interferencyjna jest praktycznie niewidoczna w skali wykresu, choć może się ujawnić podczas obserwacji w zaciemnionej pracowni.

Pytania i problemy

W jaki sposób, korzystając ze zjawiska dyfrakcji, możemy wyjaśnić, że na gruncie optyki geometrycznej wolno posługiwać się pojęciem promienia świetlnego poruszającego się wzdłuż określonych linii, mimo że światło ma charakter falowy?
Z jakiej zasady wynika obraz dyfrakcyjny światła za pojedynczą szczeliną? Narysuj schemat powstawania minimów i maksimów natężenia światła.