9.2. Drugie prawo Maxwella (temat nadobowiązkowy)
Drugie prawo Maxwella jest bardzo istotnym uzupełnieniem prawa Ampère'a. Maxwell odkrył to prawo, wychodząc z założenia, że przyroda „lubi symetrię”, czyli na drodze „rozumowania przez symetrię”. Już nieraz w historii fizyki takie rozumowanie przyniosło nadspodziewanie dobre wyniki. Tak też stało się i tym razem. Maxwell odkrył zupełnie nowe prawo przez czysto teoretyczne rozumowanie, które nie było nawet sygnalizowane żadnym doświadczeniem.
Spójrzmy jeszcze raz na pierwsze prawo Maxwella (9.3):
Wyraża ono myśl, że zmienne pole magnetyczne wywołuje wirowe pole elektryczne. Maxwell, „rozumując przez analogię”, zapytał: Czy istnieje prawo odwrotne? Czy zmienne pole elektryczne może wywołać wirowe pole magnetyczne?
Korzystając z analogii do (9.3), to „nowe” prawo należało napisać w następujący sposób:
gdzie jest pewnym współczynnikiem potrzebnym do uzgodnienia jednostek. Wzór (9.3) należałoby czytać następująco: cyrkulacja pola magnetycznego indukowanego przez zmienne pole elektryczne jest równa szybkości zmian strumienia pola elektrycznego mnożonego przez pewien stały współczynnik .
Współczynnik we wzorze (9.3) wyraża się za pomocą wzoru:
W ogólnym przypadku, gdy w układzie występuje zarówno zmienny strumień pola elektrycznego, jak i przepływa prąd elektryczny, drugie prawo Maxwella ma postać:
Słowami można to ująć następująco:
Jak widzimy, drugie prawo Maxwella jest uogólnieniem prawa Ampère’a. Uogólnienie to jest bardzo ważne – zawiera istotną nowość.
Zwróćmy uwagę na to, że przy szybkości zmiany strumienia pola elektrycznego w drugim prawie Maxwella (9.4) występuje znak „+”, podczas gdy znak przy szybkości zmian strumienia pola magnetycznego w pierwszym prawie Maxwella (9.3) to „–”. Wynika to z zasady zachowania energii. Gdyby znaki w obu przypadkach były jednakowe, wówczas bardzo mały wzrost natężenia jednego pola powodowałby wzrost drugiego, co z kolei pociągałoby wzrost pierwszego itd. W konsekwencji prowadziłoby to do nieograniczonego wzrostu obu pól; i na odwrót, bardzo małe zmniejszenie jednego pola wywołałoby całkowity zanik obu pól.
Widzimy, że mimo wszystko prawa te wykazują asymetrię wynikającą z braku oddzielnych biegunów magnetycznych („monopoli”, których dotychczas nie odkryto, mimo intensywnych poszukiwań). Gdyby one istniały, to równania te osiągnęłyby pełną symetrię, gdyż w prawie pierwszym pojawiłby się wyraz, który miałby interpretację „prądu magnetycznego”, analogiczny do wyrazu z prądem elektrycznym występującym w prawie drugim.
Z praw Maxwella wynika, że jeżeli w próżni wytworzymy zmienne pole magnetyczne, to wywoła ono wirowe pole elektryczne (pierwsze prawo Maxwella), które jest na ogół zmienne. To zmienne pole elektryczne wytworzy (zgodnie z drugim prawem Maxwella) nowe zmienne pole magnetyczne, a to z kolei wytworzy nowe pole elektryczne itd. Widać zatem, że wystarczy wytworzyć w jakimś miejscu przestrzeni zmienne pole magnetyczne (czy elektryczne), aby rozpoczął się „taniec” rozchodzących się w przestrzeni pól – elektrycznego i magnetycznego. Ten „taniec” to nic innego, jak fala elektromagnetyczna mknąca w przestrzeni z olbrzymią prędkością, tj. z prędkością światła. Zagadnienie to rozważymy dokładniej w rozdziale 10.2. Relatywistyczna zależność pól magnetycznego i elektrycznego (temat nadobowiązkowy).
Pytania i problemy
- Wyjaśnij, na czym polega symetria występująca między pierwszym a drugim prawem Maxwella.
- Podaj drugie prawo Maxwella oraz zapisz je w postaci wzoru. Wytłumacz, jaki ma ono związek z prawem Ampere'a.
- Obwód przedstawiony na il. 9.4 służy do
ładowania kondensatora
przez opornik
. Po zamknięciu klucza
w obwodzie płynie prąd o początkowym natężeniu
; wraz z upływem czasu natężenie to maleje. Uzasadnij, powołując
się na właściwe prawo Maxwella, że w obszarze między okładkami kondensatora
występuje pole magnetyczne, które znika wraz z zakończeniem procesu
ładowania.
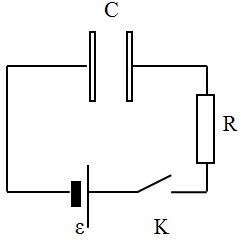 Ilustracja 9.4. Obwód ładowania kondensatora przez opornik
Ilustracja 9.4. Obwód ładowania kondensatora przez opornik - Dlaczego fizycy przedsięwzięli wiele wysiłków, aby znaleźć „monopole” magnetyczne? Jak zmieniłyby się prawa Maxwella, gdyby one istniały? Spróbuj sam napisać takie „zmienione prawa Maxwella”.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
