5.1. Oscylator harmoniczny
Z drganiami mechanicznymi mamy do czynienia na co dzień. We wstępie do tego rozdziału podaliśmy wiele przykładów ruchu drgającego. Położenie ciała w takim ruchu często zmienia się w czasie zgodnie z funkcją sinus lub kosinus, które nazywają się funkcjami harmonicznymi. Dlatego drgania takie nazywamy drganiami harmonicznymi. Ciało, którego położenie zmienia się w czasie jak funkcja harmoniczna sinus lub kosinus, nazywamy oscylatorem harmonicznym.
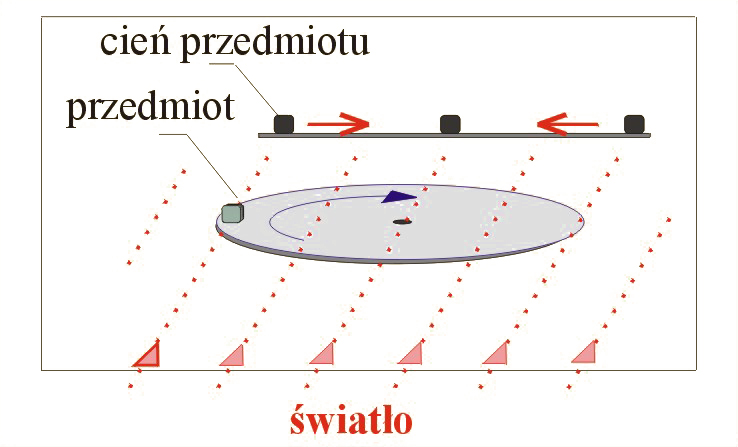
Na il. 5.1 pokazano kolejny przykład ruchu drgającego harmonicznego – ruch cienia małego przedmiotu położonego na ruchomej tarczy gramofonu.
Położenie ciała wykonującego drgania
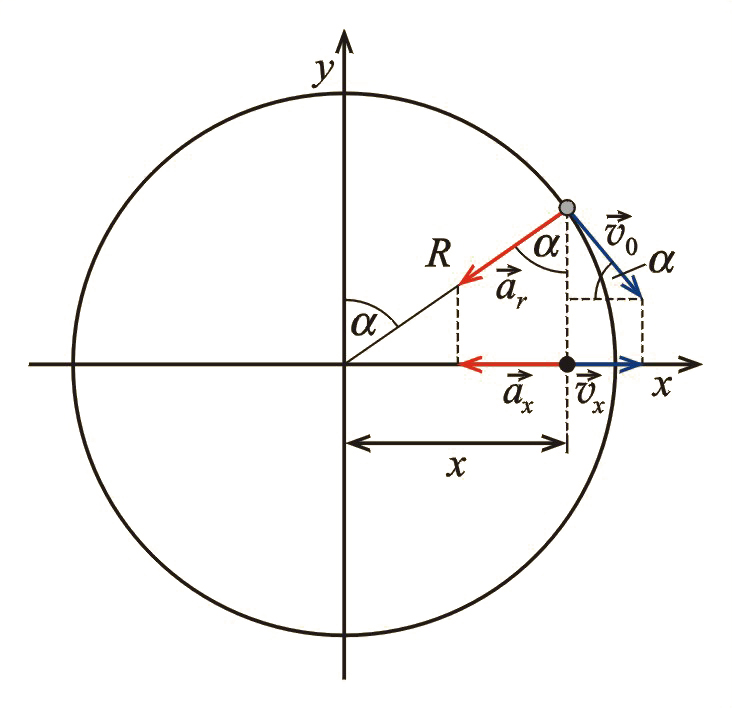
Innym przykładem jest ruch rzutu punktu poruszającego się ruchem jednostajnym po okręgu na średnicę tego okręgu (il. 5.2). Na rysunku widać, że stosunek współrzędnej tego punktu do promienia jest równy sinusowi kąta . Możemy zatem tę współrzędną wyrazić w postaci:
(gdyż zmienia się w czasie według równania , gdzie jest prędkością kątową). Widzimy więc, że położenie punktu drgającego (rzutu punktu poruszającego się po okręgu) zmienia się w czasie według funkcji sinus.
Pojęcia podstawowe
Zdefiniujemy teraz odpowiednie wielkości charakteryzujące ruch drgający:
- amplituda – wartość bezwzględna maksymalnego wychylenia ciała drgającego od położenia zerowego, tzn. (w przypadku pokazanym na il. 5.2 , gdzie – promień okręgu);
- okres – odcinek czasu, po którego upływie drganie się powtarza, czyli punkt drgający przechodzi przez to samo położenie i w tym samym kierunku;
- częstotliwość
– jest to liczba pełnych drgań w jednostce czasu (np. w 1
sekundzie); oczywiście:
( 5.2 )
- częstość kołowa
– mówi nam, ile pełnych drgań oscylator wykonuje w ciągu
jednostek czasu (np.
sekund), czyli jest to częstotliwość mnożona przez
:
( 5.3 )
Ostatnie trzy wielkości są równe liczbowo swoim odpowiednikom w ruchu po okręgu, gdzie między nimi występują takie same związki (rozdział 1.3 Ruch jednostajny po okręgu).
Gdy we wzorze (5.1) podstawimy , otrzymamy wzór ogólny na położenie ciała w ruchu drgającym harmonicznym:
Zmienna , będąca argumentem funkcji sinus, nazywa się fazą drgań. Ze wzoru wynika, że wychylenia ciała drgającego zmieniają się okresowo i spełniają warunek .
Prędkość i przyspieszenie w ruchu harmonicznym
Jaką zależnością od czasu wyrazi się w tym ruchu prędkość? Oczywiście, rzut punktu na oś będzie się poruszał z prędkością równą rzutowi wektora prędkości po okręgu na tę oś. Na il. 5.2 widzimy, że , więc:Ponieważ: ,
Zatem:
Stąd wynika, że prędkość w ruchu harmonicznym także zmienia się okresowo. Największą wartość przyjmuje dwukrotnie w ciągu okresu – dla i dla , tj. gdy położenie chwilowe ciała . Najmniejszą wartość osiąga dla i , gdy ciało znajduje się w skrajnych położeniach i zawraca; wtedy lub .
Ponieważ prędkość ciała w tym ruchu ciągle się zmienia, więc musi występować przyśpieszenie. Jest ono równe rzutowi przyśpieszenia dośrodkowego na oś (il. 5.2), więc:
Skoro:
to:
Po uwzględnieniu (5.4) otrzymamy:
Znak „–” występujący w tym wzorze informuje nas, że przyśpieszenie w ruchu drgającym jest zwrócone przeciwnie do wychylenia, tzn. że jeżeli wychylenie ma wartość dodatnią, to przyśpieszenie jest zwrócone w stronę ujemnych wartości , jeżeli wychylenie ma wartość ujemną, to przyśpieszenie jest zwrócone w stronę dodatnich wartości . Maksymalną wartość przyśpieszenia ciało drgające ma wtedy, gdy znajduje się w skrajnych położeniach.
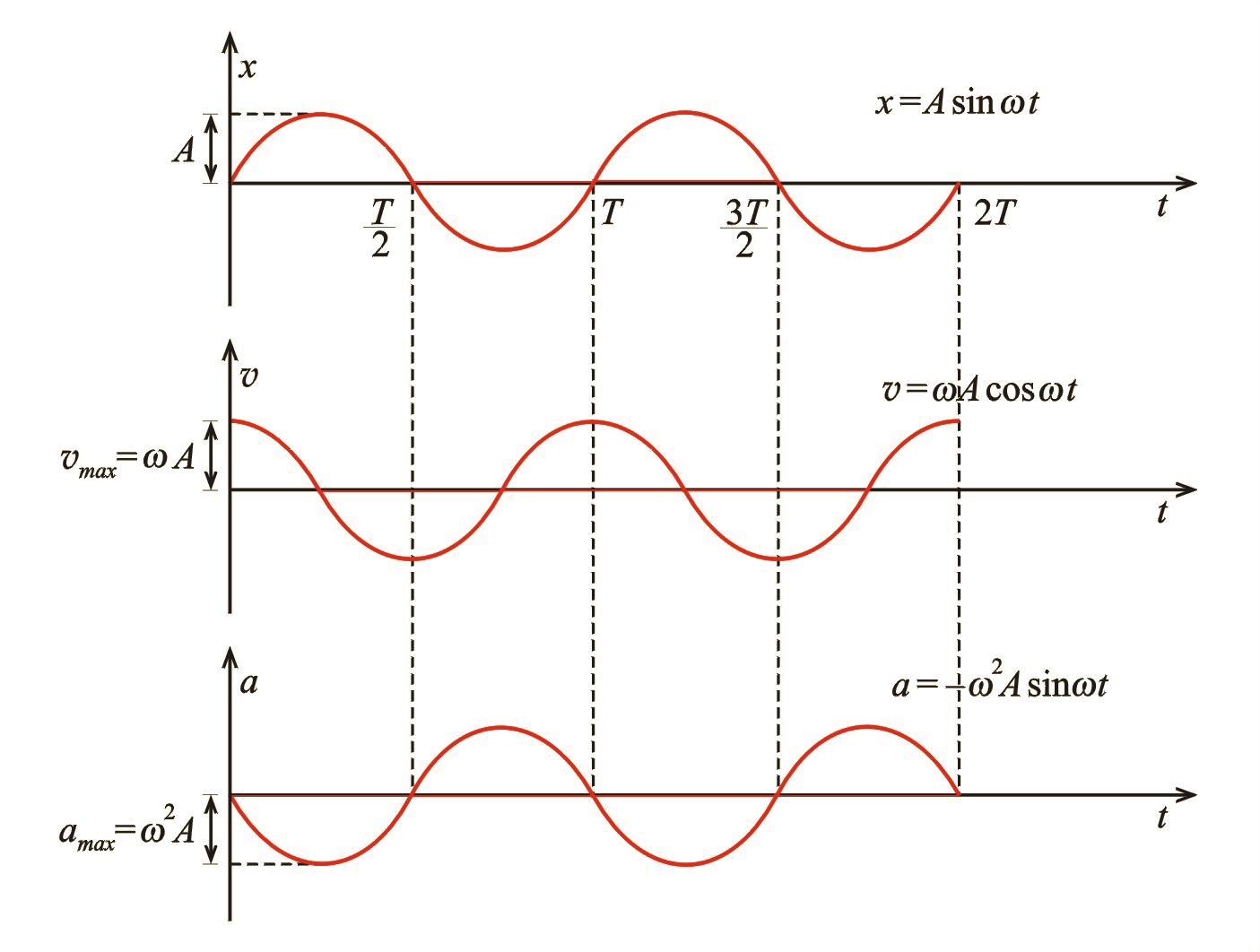
Wykresy tych zależności zostały przedstawione na il. 5.3. Widzimy, że dla oscylatora harmonicznego w stosunku do wychylenia prędkość jest przesunięta w fazie o , natomiast przyśpieszenie – o .
Siła kwazisprężysta. Położenie równowagi
Jeżeli drgania harmoniczne są wykonywane przez ciało o masie (np. przez ciężarek o masie zawieszony na lekkiej sprężynie), to przyśpieszenie jest wywoływane przez siłę . Stosując wzór (5.11), otrzymujemy:
Widzimy, że siła ta jest proporcjonalna do wychylenia i ma znak przeciwny do wychylenia, czyli jest podobna do siły sprężystej (rozdział 3.2 Energia potencjalna), opisanej w prawie Hooke'a:
Dlatego siłę występującą w oscylatorze harmonicznym nazywamy siłą kwazisprężystą (łac. quasi znaczy jak gdyby) lub harmoniczną. Siła kwazisprężysta w różnych układach może być realizowana w różny sposób. Stały współczynnik zależy od sposobu realizacji tej siły. Możemy stwierdzić, że jeżeli na jakieś ciało działa siła kwazisprężysta , to może ono wykonywać drgania harmoniczne.
Na podstawie porównania wzorów (5.12) i (5.13) wnioskujemy, że:
Z tego wzoru wynika, że częstość drgań zależy tylko od własności samego oscylatora – jego masy i sprężystości, dlatego częstość tę nazywamy częstością własną oscylatora i oznaczamy przez . Zatem:
Stąd częstość kołowa tych drgań wynosi:
Jest to bardzo użyteczny wzór, gdyż pozwala obliczyć częstość drgań układu w wielu przypadkach, gdy zależność siły od położenia jest typu (5.13) i znany jest stały współczynnik .
Zgodnie ze wzorami (5.15) i (5.3) okres drgań własnych wynosi:
Przykład 1
Ciężarek o masie zawieszony na sprężynie o współczynniku sprężystości został wprawiony w drgania. Zaniedbując tłumienie drgań, oblicz częstotliwość własną i okres drgań ciężarka.
Rozwiązanie: Za pomocą wzoru (5.15) należy obliczyć częstość kołową, a następnie, korzystając z zależności , częstotliwość własną :
Zatem ciężarek wykonuje „1/2 drgnięcia na 1 sekundę”, czyli 5 drgań na 10 sekund, więc okres wynosi .
Doświadczenie „Sprężyna”
Wykazaliśmy wyżej, że jeżeli na ciało działa siła kwazisprężysta, ciało to może drgać ruchem harmonicznym. Wynika stąd, że jeżeli ciężarek doczepimy do sprężyny, to będzie mógł wykonywać drgania harmoniczne, gdyż będzie działać nań siła sprężysta. Obecnie przeprowadzimy eksperyment potwierdzający w sposób poglądowy ten wniosek. Podobnie jak pokazano na il. 5.1, będziemy jednocześnie obserwować ruch cienia przedmiotu znajdującego się na tarczy gramofonu i ruch cienia ciężarka doczepionego do sprężyny (il. 5.4). W tym celu umieszczamy ciężarek na wózku toru powietrznego. Do wózka z ciężarkiem doczepiamy sprężynę, której drugi koniec mocujemy do nieruchomego statywu toru. Wózek z ciężarkiem pobudzamy do drgań. Dostosowując częstotliwość obrotów tarczy gramofonu, możemy doprowadzić do synchronizacji ruchu cienia przedmiotu (znajdującego się na tarczy) z ruchem cienia ciężarka drgającego na sprężynie.
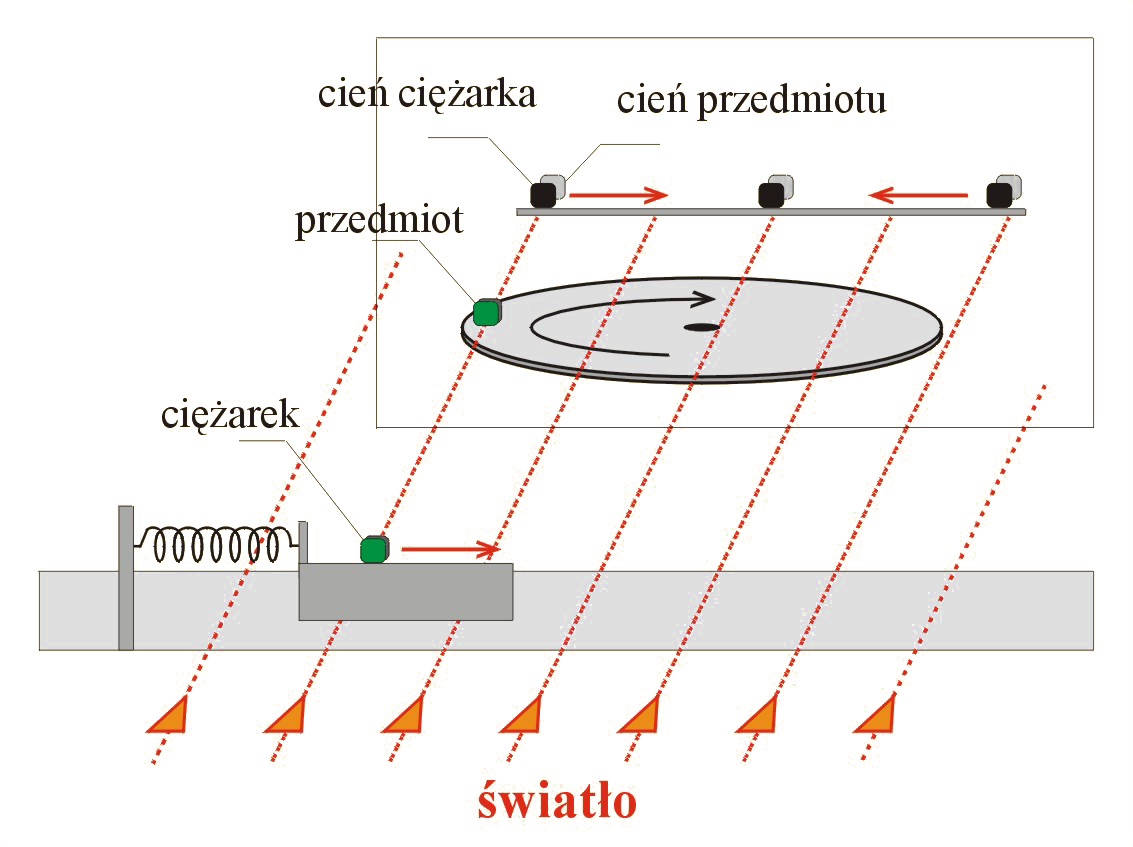
Wiemy, że ruch cienia przedmiotu znajdującego się na tarczy gramofonu jest ruchem harmonicznym (odbywa się według zależności odpowiadającej funkcji harmonicznej sinus lub kosinus). Możliwość synchronizacji ruchu ciężarka na sprężynie z ruchem cienia przedmiotu na tarczy świadczy o tym, że ciężarek na sprężynie także wykonuje drgania harmoniczne.
Zatem w tym doświadczeniu wykazaliśmy ogólną prawidłowość, że układ pod wpływem siły kwazisprężystej wykonuje drgania harmoniczne – również ciężarek pod wpływem siły sprężystej.
Jeżeli nie dysponujemy torem powietrznym, doświadczenie to możemy wykonać inaczej. Sprężynę z ciężarkiem zawieszamy pionowo na statywie. Również pionowo ustawiamy tarczę gramofonu z przymocowanym do niej przedmiotem. Podobnie jak poprzednio, doprowadzamy do synchronizacji ruchu cieni.
Pytania i problemy
- Scharakteryzuj ruch wykonany przez oscylator harmoniczny.
- Podaj definicje: amplitudy, okresu, częstotliwości, częstości kołowej.
- Przedstaw i opisz zależność maksymalnej prędkości w ruchu drgającym harmonicznym od amplitudy drgań i częstotliwości.
- Napisz równanie przedstawiające zależność chwilowej wartości przyśpieszenia od chwilowej wartości wychylenia w ruchu drgającym harmonicznym. W jakim położeniu znajduje się ciało drgające, gdy przyśpieszenie osiąga maksymalną wartość? Jaka jest wtedy prędkość tego ciała?
- Wyjaśnij, co to znaczy, że wychylenie i prędkość w danej chwili ruchu drgającego harmonicznego są przesunięte w fazie. Czy przesunięcie fazowe między wychyleniem i przyspieszeniem ma taką samą wartość, jak między wychyleniem i prędkością? Podaj wartość tych przesunięć.
- Czym charakteryzuje się siła, którą nazywamy siłą kwazisprężystą? Przedstaw tę siłę za pomocą wzoru, wyjaśnij znaczenie symboli.
- Między dwiema równiami pochyłymi toczy się kulka (il. 5.5), zatrzymując się przed dotarciem na szczyt każdej
z nich (pomijamy rozpraszanie energii w ruchu kulki). Czy ruch ten
jest ruchem drgającym? Czy można mu przypisać amplitudę, okres, częstotliwość,
maksymalną prędkość? Czy jest to ruch harmoniczny prosty? Uzasadnij swoje
odpowiedzi.
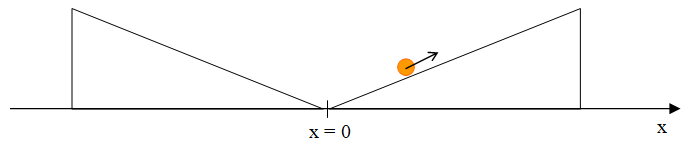 Ilustracja 5.5. Kulka toczy się bez rozpraszania energii między dwiema równiami pochyłymi
Ilustracja 5.5. Kulka toczy się bez rozpraszania energii między dwiema równiami pochyłymi


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
