Powtórzymy słynne doświadczenie ze swobodnie spadającymi ciałami, przeprowadzone przez Galileusza.

Przygotujmy kilka ciężarków o różnych masach (będziemy je puszczać z wysokości $h$), kilka stoperów do pomiaru czasu spadania ciężarków (mogą to być stopery w telefonach komórkowych) oraz taśmę mierniczą do pomiaru wysokości $h$. Doświadczenie wykonujemy w następujący sposób:

Najpierw mierzymy wysokość $h$, z której będziemy spuszczać ciężarki (może to być wysokość drugiego lub trzeciego piętra budynku). Pamiętajmy także o zabezpieczeniu przewidywanego miejsca upadku ciężarków czymś miękkim, by nie zniszczyć podłoża. Następnie na dany sygnał (np. przez nauczyciela) jeden uczeń puszcza ciężarek, a inni stoperami mierzą czas jego spadania. Te same czynności powtarzamy z innymi ciężarkami.

Po zakończeniu pomiarów wykonamy jeszcze jedno doświadczenie: Wszystkie ciężarki (o różnych masach) puścimy jednocześnie i zwrócimy uwagę na to, czy ciężarki upadły na ziemię w tej samej chwili.

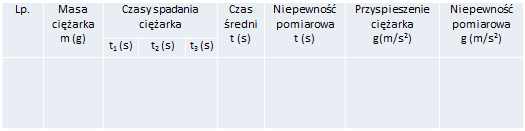
Wyniki pomiarów zapisujemy w tabelce przygotowanej według wzoru przedstawionego na il. 1.20. Jeżeli czas spadania ciężarków jest mierzony przez więcej niż troje uczniów, to odpowiednio zwiększamy liczbę kolumn w tabeli.

Oceniamy niepewności pomiarów zgodnie z opisem w rozdziale 1.7. Ocena niepewności pomiarowych. Najpierw oceniamy niepewność pomiaru czasu średniego $t$ jako sumę wartości najmniejszej działki stopera (np. 0,1 s) i czasu reakcji przy włączaniu i wyłączaniu stopera (np. 2 razy 0,1 s + 0,1 s, więc w sumie $\Delta t=\mathrm{0,3}\text{s}$).

Musimy przy tej okazji krytycznie spojrzeć na uzyskane pojedyncze wyniki czasu spadania i rozstrzygnąć, czy któryś z nich nie jest obarczony błędem grubym, czy nie jest efektem pomyłki. Sprawdzamy zatem, czy każdy pojedynczy pomiar odstaje od średniej w swojej serii nie bardziej niż o $\Delta t$. Jeżeli wychwycimy wynik, który nie mieści się w przedziale $t_{\text{śr}}\pm \Delta t$, to powinniśmy rozważyć jego wyeliminowanie z serii i ponowne obliczenie wartości $t_{\text{śr}}$.

Odpowiadamy na pytanie, czy czas spadania ciężarków o różnych masach jest jednakowy w granicach niepewności pomiarowej. Jaki wypływa stąd wniosek?

Oceńmy teraz niepewność pomiarową wysokości $\Delta h$. Musimy uwzględnić, że ciężarki mogliśmy spuszczać z nieco różniących się wysokości (przyjmujemy, że niepewność stąd wynikająca nie przekracza 2 cm). Ponadto podłoże, na które spadały ciężarki, nie jest idealnie poziomą płaszczyzną (np. różnice wysokości mogły wynosić 3 cm). Dokładność przyłożenia taśmy mierniczej oraz ograniczona dokładność taśmy (wartość najmniejszej działki taśmy mierniczej) powiększa nam niepewność pomiarową (np. o dodatkowe: 1 cm + 1 cm = 2 cm). Przyjmujemy, że wszystkie te wartości, po zsumowaniu, dają łączną wartość niepewności pomiaru wysokości $h$ (w naszym przykładzie $\Delta h=2\text{cm}+3\text{cm}+2\text{cm}=7\text{cm}$).

Obliczamy niepewność pomiaru przyspieszenia ziemskiego $g$, korzystając z reguły podanej w rozdziale 1.7. Ocena niepewności pomiarowych. W naszym przypadku niepewność względną wyniku pomiaru obliczamy według wzoru:

Sprawdzamy, czy otrzymane wartości $g$ dla różnych mas ciężarków różnią się między sobą w granicach obliczonej niepewności pomiarowej. Obliczamy wartość średnią $g_{\text{śr}}$.

Oblicz różnicę między $g_{\text{śr}}$ a znaną wartością $g=\mathrm{9,81}\text{m}/{\text{s}}^2$ (tablicową). Jaki wynika stąd wniosek?

Jako podsumowanie doświadczenia zapisujemy zasadniczy wniosek końcowy: co było celem doświadczenia i czy wyniki pomiarów są zgodne z naszymi oczekiwaniami uwzględnionymi w opisie celu doświadczenia.