Zasada ekwipartycji energii

Wiemy, że wszystkie cząsteczki gazu w takiej samej temperaturze mają jednakową średnią energię kinetyczną ruchu postępowego, niezależnie od wielkości ich mas. W przypadku gazu mającego cząsteczki w postaci pojedynczych atomów (tzw. gazu jednoatomowego) braliśmy pod uwagę tylko energię ruchu postępowego. Nie musieliśmy uwzględniać energii ruchu obrotowego. Energię ruchu obrotowego atomu można zaniedbać, gdyż jego masa jest głównie skoncentrowana w jądrze, którego rozmiary są setki tysięcy razy mniejsze od rozmiarów całego atomu (dlatego moment bezwładności atomu jest bardzo mały). Nie możemy jednak zaniedbać ruchu obrotowego cząsteczek składających się z dwóch i więcej atomów, gdyż w tym przypadku energia ruchu obrotowego jest porównywalna z energią kinetyczną ruchu postępowego.

W celu uwzględnienia energii ruchu obrotowego cząsteczek wprowadzimy pojęcie liczby stopni swobody cząsteczki. Jest to najmniejsza liczba niezależnych współrzędnych, które należy podać, aby jednoznacznie określić położenie cząsteczki w przestrzeni.

W przypadku pojedynczego atomu, którego rozmiary możemy zaniedbać i który redukujemy do punktu materialnego, liczba stopni swobody jest równa 3, ponieważ do określenia jego położenia wystarczy podać trzy współrzędne: $x$, $y$ i $z$. Według równania (6.34):

średnia energia kinetyczna ruchu postępowego wynosi $\frac{3kT}{2}$. Średni kwadrat prędkości można wyrazić za pomocą trzech składowych:

Ze względu na to, że żaden z kierunków $x$, $y$, $z$ nie jest wyróżniony, możemy przyjąć, że wszystkie trzy składowe prędkości średniej są jednakowe, czyli:

gdzie wskaźnik $i$ oznacza $x$, $y$ lub $z$. Zatem na podstawie wzoru (7.46) mamy:

Wnioskujemy stąd, że na jedną składową prędkości, czyli na jeden stopień swobody, przypada średnio energia kinetyczna równa:

Wniosek ten można uogólnić na cząsteczki o dowolnej liczbie stopni swobody, mogące wykonywać nie tylko ruchy postępowe, ale też rotacyjne (obrotowe) i drgające. Wniosek można przedstawić w postaci zasady ekwipartycji energii, która brzmi:

Należy podkreślić, że zasada ekwipartycji energii ma charakter statystyczny – dotyczy wartości średnich dużej liczby cząsteczek.

Energia wewnętrzna gazu składającego się z cząsteczek o liczbach swobody $i>3$

Zasada ekwipartycji energii pozwala obliczyć energię wewnętrzną gazu złożonego z cząsteczek, z których każda ma $i$ stopni swobody. W rozdziale Energia wewnętrzna, ciepło i praca podaliśmy wzór (7.2) na energię wewnętrzną gazu przy założeniu, że składa się na nią tylko energia kinetyczna $N$ jednakowych cząsteczek gazu, z których każda ma tylko $i=3$ stopni swobody:

W ogólnym przypadku średnia energia kinetyczna jednej cząsteczki wynosi:

Zatem energia wewnętrzna gazu, tj. energia kinetyczna wszystkich $N$ cząsteczek, wynosi:

Rozważymy teraz działanie zasady ekwipartycji energii w następujących przypadkach:

1. Gaz jednoatomowy składa się z cząsteczek mających 3 stopnie swobody. Energię wewnętrzną $N$ cząsteczek gazu, określoną jako suma energii kinetycznych cząsteczek, można wyrazić jako iloczyn średniej energii kinetycznej cząsteczek równej $\frac{3kT}{2}$ i liczby cząsteczek $N$:

2. Gaz dwuatomowy składa się z cząsteczek mających w uproszczeniu kształt hantli (dwie kule połączone sztywnym prętem) – il. 7.25. Dla takiej cząsteczki przyjmujemy pięć stopni swobody $\left(i=5\right)$, czyli trzy współrzędne określające położenie środka masy oraz dwie współrzędne określające jej obrót względem osi $O\text{'}-O\text{'}$ i prostopadłej do niej osi $O\text{'}\text{'}-O\text{'}\text{'}$. Trzeciej osi $O\text{'}\text{'}\text{'}-O\text{'}\text{'}\text{'}$ nie uwzględniamy, gdyż energia kinetyczna obrotu cząsteczki względem tej osi jest zaniedbywalnie mała w stosunku do energii obrotu cząsteczki względem dwóch pozostałych osi. Zatem energia wewnętrzna gazu wynosi:

3. Gaz trzyatomowy składa się z cząsteczek mających kształt zbliżony do trójkąta (il. 7.26). Dla takiej cząsteczki przyjmujemy sześć stopni swobody $\left(i=6\right)$: trzy współrzędne środka masy oraz trzy współrzędne obrotu względem trzech prostopadłych osi. Zatem energię wewnętrzną takiego gazu, zgodnie ze wzorem (7.50) można wyrazić następująco:

Zasada ekwipartycji energii pozwala teoretycznie przewidzieć wartość ciepła właściwego oraz współczynnika Poissona $\kappa$ dla różnych gazów. Zgodnie z definicją (7.18):

gdzie $c_V$ – ciepło właściwe gazu przy stałej objętości, $C_V$ – ciepło molowe gazu przy stałej objętości, $c_p$ – ciepło właściwe gazu przy stałym ciśnieniu, $C_p$ – ciepło molowe gazu przy stałym ciśnieniu.

Obliczymy najpierw ciepło molowe przy stałej objętości. Wykorzystamy wzór (7.9), wyrażający zmianę energii wewnętrznej pod wpływem przyrostu temperatury gazu o $\Delta T$:

Zatem zmiana energii wewnętrznej dla jednego mola gazu wynosi:

gdzie $\mu$ – masa jednego mola gazu; wykorzystano tu również wzór (7.16), czyli:

Wcześniej wyprowadziliśmy wzór (7.50) na energię wewnętrzną gazu zawierającego cząsteczki o $i$ stopniach swobody. Zatem przy zmianie temperatury o $\Delta T$ przyrost energii wewnętrznej dla jednego mola gazu wynosi:

gdzie $N_A$ jest liczbą cząsteczek w jednym molu – liczbą Avogadra. Ponieważ $N_{A}k=R$, więc:

Po porównaniu wzorów (7.55) i (7.56) otrzymamy:

Zgodnie z równaniem Mayera (7.17) $C_p=C_V+R$, więc $C_p=\frac{i}{2}R+R$. Zatem:

Po podzieleniu stronami równań (7.58) i (7.57) otrzymujemy, współczynnik Poissona:

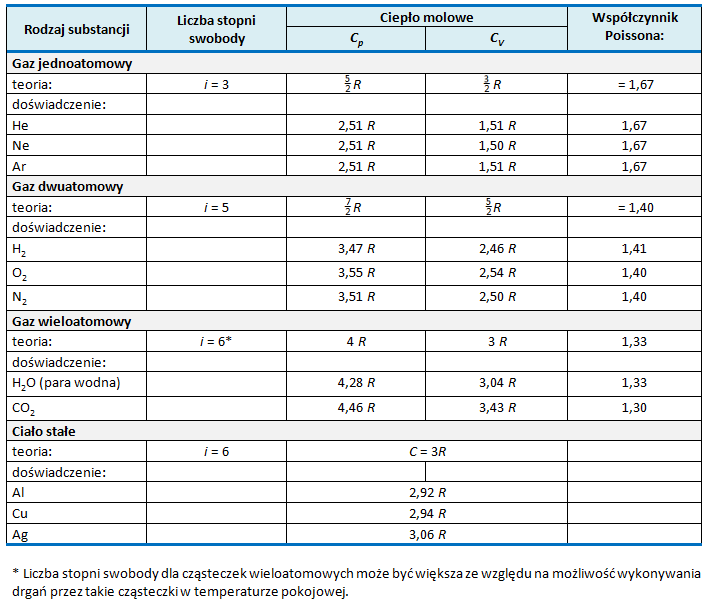
Widzimy zatem, że teoria kinetyczna pozwala przewidzieć, ile powinny wynosić ciepła molowe $C_V$ i $C_p$ oraz współczynnik Poissona dla dowolnego gazu, jeżeli wiadomo, z jakich cząsteczek składa się dany gaz. W tabeli na il. 7.27 zestawiono wyniki teoretyczne z wynikami otrzymanymi doświadczalnie dla różnych gazów rzeczywistych. Oprócz tego w tabeli zamieszczono doświadczalne wartości $C$ dla ciał stałych (wyjaśnienie wartości teoretycznej $C$ dla ciał stałych znajduje się w przykładzie D1). Jak widać, zgodność teorii z wynikami doświadczeń jest dobra, szczególnie dla gazów jedno- i dwuatomowych.

Wyprowadzenie wzoru na pracę w przemianie adiabatycznej

Cząsteczki o większej liczbie atomów, traktowane jako bryły sztywne, mają oczywiście również sześć stopni swobody. Zatem dla gazów złożonych z trzech i więcej atomów energia wewnętrzna wyraża się również za pomocą wzoru (7.52).

Na podstawie wzoru (7.50) przyrost energii wewnętrznej gazu, przy wzroście temperatury o $\Delta T=T_2–T_1$, możemy wyrazić następująco:

Wobec tego praca $W$ w procesie adiabatycznym, zgodnie z (7.31), wyrazi się wzorem:

Z prawa gazu doskonałego (6.29) otrzymamy $\Delta W=\frac{i}{2}\left(p_1{V}_1-p_2{V}_2\right)$. Ponadto łatwo można wykazać, korzystając ze wzoru (7.59), że $\frac{i}{2}=\frac{1}{\kappa -1}$. Dzięki temu ostatecznie otrzymamy następujący wzór na pracę w procesie adiabatycznym: