5.4. Reguła Titiusa-Bodego - temat nadobowiązkowy
Johann Titius, fizyk urodzony (w XVIII w.) w Chojnicach na Pomorzu, wydedukował, korzystając z prawa grawitacji, że średnie odległości planet od Słońca (wyrażone w AU – jednostkach astronomicznych) dla Merkurego i kolejnych planet, aż do Saturna włącznie, spełniają warunek:
gdzie przybiera wartości 0, 1, 2, 4, 8, 16, 32 (reguła ta jest zwana regułą Titiusa-Bodego). Warto zauważyć, że z wyjątkiem zera wszystkie pozostałe liczby są potęgami liczby 2, i tak:
Titius sprawdził swoją formułę tylko dla planet, które w owym czasie były znane – patrz tabela na il. 5.12.
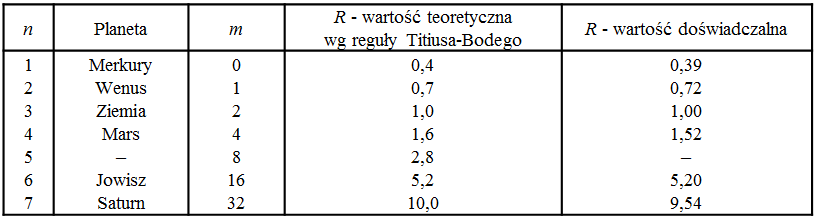
Okazało się, że formuła ta jest prawdziwa z zupełnie dobrą dokładnością, dla wszystkich znanych w owym czasie planet. Brakowało jednak planety odpowiadającej liczbie , planety, której orbita powinna się znajdować między orbitami Marsa i Jowisza w odległości 2,8 AU od Słońca. Dopiero w XIX i XX wieku odkryto wiele drobnych ciał, tzw. planetoid, mających właśnie orbity o średnich promieniach zbliżonych do wartości 2,8 AU. Wiele obecnych danych obserwacyjnych świadczy o tym, że planetoidy te są prawdopodobnie pozostałością po rozbitej planecie, która miała tam swoją orbitę.
A co z pozostałymi planetami i innymi ciałami niebieskimi, które odkryto później – Uranem, Neptunem i Plutonem (24 sierpnia 2006 r. Międzynarodowa Unia Astronomiczna odebrała Plutonowi status planety i zaliczyła do tzw. planet karłowatych)?
Uzupełnimy tabelę, korzystając z następujących liczb dla:
Urana
Plutona
(nie uwzględniamy Neptuna, który ma nietypową orbitę).

Zgodnie ze wzorem (5.21) promień orbity Urana wynosi:
zaś promień orbity Plutona wynosi:
Widzimy, że te planety, z wyjątkiem Neptuna, również poruszają się realnie po orbitach odpowiadających formule Titiusa-Bodego.
Obecne poglądy na temat teoretycznego uzasadnienia reguły Titiusa-Bodego opierają się na modelach powstawania pierwotnych układów planetarnych i nadal stanowią przedmiot dociekań współczesnych astronomów. Więcej informacji na ten temat znajdziesz w Internecie.
Pytania i problemy
- Podaj wzór Titiusa-Bodego na średnią odległość planet od Słońca i objaśnij znaczenie symboli w tym wzorze.
- Jak wiadomo, formuła Titiusa-Bodego sprawdziła się z dobrą dokładnością dla wszystkich znanych w owym czasie planet z wyjątkiem odpowiadającej liczbie planety, której orbita powinna się znajdować między orbitami Marsa i Jowisza. Jakie odkrycie uzasadniło prawdziwość tej formuły dla tej liczby?
- Czy formuła Titiusa-Bodego sprawdza się również dla planet nieznanych w ich czasach? Podaj nazwy tych planet oraz ich numerację zgodną z tą formułą.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
