Korzystając z równania stanu gazów doskonałych (6.12), możemy znaleźć zależność objętości gazu od temperatury przy stałym ciśnieniu $p=p_c=\text{const}$. Załóżmy, że w temperaturze zera stopni Celsjusza $t_0=0°\text{C}$ $\text{(}{T}_0=\mathrm{273,15}\text{K}\text{)}$ gaz ma objętość $V_0$. Wtedy:

natomiast przy innej temperaturze $T$ gaz zajmuje objętość $V$, zatem:

Po podzieleniu równania (6.21) przez (6.20) otrzymamy:

lub:

Korzystając ze wzoru (6.5): $T=\mathrm{273,15}+t=T_0+t$, przechodzimy do skali Celsjusza. Zatem:

Jeżeli przyjmiemy oznaczenie:

to ostatecznie otrzymamy:

Wzór w tej postaci określa rozszerzalność objętościową gazów przy stałym ciśnieniu. Współczynnik $\alpha$ nazywa się współczynnikiem rozszerzalności objętościowej i dla gazów doskonałych przy stałym ciśnieniu jego wartość wynosi:

Dlaczego gaz zwiększa swoją objętość przy stałym ciśnieniu podczas podwyższania temperatury? Wzrost temperatury gazu jest równoznaczny ze zwiększeniem średniej energii kinetycznej cząsteczek, a więc i prędkości cząsteczek. Zatem cząsteczki uderzają w ścianki naczynia z większą prędkością, przy każdym odbiciu doznają większej zmiany pędu i oddziałują na ścianki naczynia z coraz większą siłą. Jeżeli ciśnienie ma być stałe, a naczynie nie ulega odkształceniu, to objętość gazu musi się zwiększyć, gdyż wtedy zwiększy się pole powierzchni ścianek. Wówczas zwiększona siła działa na większą powierzchnię i ciśnienie będące stosunkiem siły do pola powierzchni, $p=\frac{F}{S}$, może utrzymać się na stałym poziomie.

Dotychczasowe doświadczenia wykazują, że wzór (6.22) obowiązuje, z dobrą dokładnością, również dla cieczy i ciał stałych. Współczynnik rozszerzalności objętościowej definiuje się, zgodnie z tym wzorem, jako:

Widzimy, że:

ma znaczenie względnej zmiany objętości przy zmianie temperatury o jeden stopień.

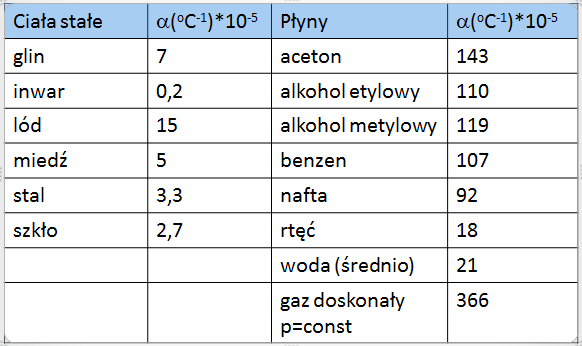
Wartość współczynnika rozszerzalności objętościowej zależy od rodzaju substancji (patrz il. 6.20). Ciała stałe mają najmniejszy współczynnik rozszerzalności objętościowej. Współczynnik ten dla cieczy jest zwykle wielokrotnie większy. Gazy mają największą rozszerzalność objętościową.

Przykład 5

Na il. 6.21 przedstawiono naczynie szklane do pomiaru gęstości cieczy, zwane piknometrem. Do piknometru nalano nieco rtęci w takiej ilości, aby wzrost objętości rtęci pod wpływem wzrostu temperatury kompensował wzrost objętości piknometru. Dzięki temu pojemność pozostałej części piknometru $V_p$ jest stała w każdej temperaturze. Piknometr napełniono alkoholem o temperaturze $t_0=0°\text{C}$. Po zważeniu stwierdzono, że masa alkoholu wynosi $m_0=40\text{g}$. Następnie piknometr z alkoholem wstawiono do zlewki z wodą o temperaturze $t=50°\text{C}$. Na skutek rozszerzalności cieplnej trochę alkoholu wylało się. Po ponownym zważeniu stwierdzono, że masa pozostałego w piknometrze alkoholu wynosi $m=\mathrm{37,9}\text{g}$. Oblicz współczynnik rozszerzalności objętościowej alkoholu.

Rozwiązanie: Najpierw wyprowadzimy wzór na zależność gęstości $\rho$ cieczy od temperatury. Wiemy, że:

$\rho =\frac{m}{V}$

i że objętość $V$ substancji zmienia się wraz z temperaturą $t$ według wzoru (6.22), przy niezmieniającej się masie $m$, więc:

$\rho =\frac{m}{V_0\left(1+\alpha t\right)}$

Ponieważ $\frac{m}{V_0}={\rho }_0$, gdzie ${\rho }_0$ oznacza gęstość cieczy w temperaturze $0°\text{C}$, więc:

$$\rho =\frac{{\rho }_0}{1+\alpha t}$$

( 6.24 )

W naszym przypadku $\rho =\frac{m}{V_p}$ oraz ${\rho }_0=\frac{m_0}{V_p}$. Po podstawieniu do wzoru (6.24), otrzymamy $m=\frac{m_0}{1+\alpha t}$. Stąd po przekształceniu:

$\alpha =\frac{m_0-m}{mt}=\frac{40-\mathrm{37,9}}{\mathrm{37,9}\cdot 50}\frac{1}{°\text{C}}\approx \mathrm{110,8}\cdot {10}^{-5}\frac{1}{°\text{C}}$

Jest to wynik, który różni się od tablicowego (il. 6.20) o mniej niż 1%.

Współczynnik rozszerzalności objętościowej dla rzeczywistych substancji jest stały tylko w przybliżeniu, dla niedużych zakresów temperatury. Dokładne pomiary wykazują, że współczynnik $\alpha$ określony wzorem (6.21) zależy od zakresu temperatury, w którym go wyznaczono. Zatem zależność (6.22) objętości od temperatury dla cieczy i ciał stałych jest liniowa tylko w przybliżeniu.

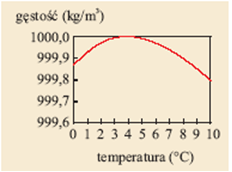
Istnieją wyjątkowe substancje, które wykazują anomalną rozszerzalność cieplną. Wśród nich na szczególną uwagę zasługuje woda. Żadna inna ciecz pospolita  nie zachowuje się anomalnie. Woda natomiast w zakresie temperatury od 0 do $4°\text{C}$ ma ujemny współczynnik rozszerzalności cieplnej, w temperaturze $4°\text{C}$ ma największą gęstość (patrz wykres – il. 6.22), a dopiero od tej temperatury wartość współczynnika $\alpha$ jest dodatnia i wraz ze wzrostem temperatury gęstość wody maleje. Dzięki tej własności wody zamarzanie stawów, jezior i rzek zaczyna się od ich powierzchni. Pozwala to przetrwać zimę rybom i innym organizmom żyjącym w wodzie.

Wzór (6.22), jak już wspomniano, stosuje się również dla ciał stałych. W praktyce bardzo często mamy do czynienia z ciałami stałymi, których jeden wymiar (najczęściej długość) jest znacznie większy od pozostałych, np. pręty, taśmy, druty czy belki. Wtedy bezwzględny przyrost długości pod wpływem temperatury jest znacznie większy od przyrostu wymiarów poprzecznych. Dlatego wprowadza się współczynnik rozszerzalności liniowej $\lambda$, który definiuje się za pomocą wzoru analogicznego do (6.23):

gdzie $l$ i $l_0$ są długościami ciała, odpowiednio, w temperaturze $t$ i $t_0=0°\text{C}$. Współczynnik rozszerzalności liniowej jest liczbowo równy względnemu przyrostowi długości ciała przypadającemu na jeden stopień.

Ze wzoru (6.25) po przekształceniu i uwzględnieniu $t_0=0°\text{C}$ otrzymujemy:

Łatwo możemy teraz wykazać, że zachodzi następujący związek między współczynnikami rozszerzalności objętościowej i liniowej:

Przyjmijmy, że $V=l^3$. Po podniesieniu równania (6.26) do trzeciej potęgi i skorzystaniu ze wzoru (6.27) otrzymamy:

Po uwzględnieniu, że $V_0=l_0^3$ i uproszczeniu otrzymamy:

Dla ciał stałych współczynnik rozszerzalności liniowej jest bardzo mały, ma wartość rzędu ${10}^{-5}÷{10}^{-6}(°\text{C}{)}^{-1}$, dlatego w wyrażeniu po lewej stronie można zaniedbać wyrazy zawierające ${\lambda }^2$ i ${\lambda }^3$ (dla małych zakresów temperatury $t<100°\text{C}$). Wtedy właśnie otrzymamy relację (6.27).

Przykład 6

Stalowe przęsło mostu (w postaci belki) ma długość $l_0=50\text{m}$ w temperaturze $0°\text{C}$. O ile wydłuży się to przęsło latem, gdy nagrzeje się na słońcu do temperatury $t=40°\text{C}$?

Rozwiązanie: Z tabeli na il. 6.20 odczytujemy wartość współczynnika rozszerzalności objętościowej stali $\alpha =\mathrm{3,3}\cdot 10^{-5}(°\text{C}{)}^{-1}$. Po podzieleniu tej wartości przez 3 otrzymujemy współczynnik rozszerzalności liniowej stali $\lambda =\mathrm{1,1}\cdot 10^{-5}(°\text{C}{)}^{-1}$. Zatem długość przęsła $l$ w temperaturze $t=40°\text{C}$ wynosi:

$l=l_0\left(1+\lambda t\right)=50\cdot \left(1+\mathrm{1,1}\cdot 10^{-5}\cdot 40\right)\text{m}=\mathrm{50,022}\text{m}$

Oznacza to, że przęsło wydłuży się o 2,2 cm. Takie wydłużenie musi być w jakiś sposób kompensowane, gdyż w konstrukcji mogą powstać niebezpieczne naprężenia.

Na zakończenie omawiania rozszerzalności cieplnej cieczy i ciał stałych zastanowimy się nad przyczynami tego zjawiska. Wiemy, że ciała stałe i ciecze należą do fazy skondensowanej i – w przeciwieństwie do gazów – odległości między cząsteczkami w tej fazie są bardzo małe. Cząsteczki i atomy w cieczach i ciałach stałych prawie stykają się ze sobą. Dlatego nie można zaniedbać sił wzajemnego oddziaływania cząsteczek.

Ciecze różnią się od ciał stałych przede wszystkim tym, że cząsteczki w cieczach mają większą swobodę ruchu. Większość ciał stałych ma strukturę krystaliczną, a to oznacza, że atomy w tych ciałach stałych mogą w zasadzie wykonywać tylko ruchy drgające wokół uporządkowanych punktów w przestrzeni, tworzących sieci krystaliczne. W cieczach natomiast pojedyncze atomy lub cząsteczki także wykonują ruchy drgające, ale mogą również stopniowo zmieniać swoje położenia (zjawisko to nazywa się autodyfuzją) i ciecz nie ma krystalicznej sieci uporządkowanych punktów.

Obecność struktury krystalicznej lub jej brak odgrywa jednak małą rolę w wyjaśnieniu rozszerzalności cieplnej. Dlatego w rozważaniach naszych zaniedbamy różnice w strukturze i własnościach cieczy i ciał stałych. Skupimy się natomiast na podstawowej własności fazy skondensowanej wynikającej z tego, że cząsteczki cieczy i ciał stałych znajdują się w bezpośredniej bliskości i mogą wykonywać drgania wokół swoich położeń równowagi.

Wzajemne odległości drgających cząsteczek średnio rosną wraz ze wzrostem temperatury. Suma odległości między cząsteczkami stanowi wymiar przestrzenny całego ciała. Skoro te odległości rosną, to rosną również wymiary przestrzenne całego ciała wraz ze wzrostem temperatury.

To, co powiedziano tutaj, tłumaczy jakościowo normalną rozszerzalność cieplną. A co z wodą? Dlaczego woda w zakresie od zera do czterech stopni zamiast się rozszerzać – kurczy? Otóż wpływ na wyjątkową, anomalną rozszerzalność wody mają akurat te zjawiska, które w naszych rozważaniach pominęliśmy, jako drugorzędne. Mianowicie, główny wpływ na pojawienie się ujemnego współczynnika rozszerzalności wody ma właśnie zmiana struktury pod wpływem wzrastającej temperatury w niedużym przedziale temperatury, powyżej punktu topnienia lodu. W lodzie atomy są ułożone luźniej niż w wodzie, dlatego lód ma mniejszą gęstość od wody. Woda, która dopiero powstała z lodu, mająca temperaturę bliską zeru stopni, częściowo zachowuje jeszcze luźniejsze ułożenie atomów charakterystyczne dla lodu. Wraz ze wzrostem temperatury ułożenia te stopniowo giną, a zaczynają przeważać ułożenia gęstsze, charakterystyczne dla stanu ciekłego wody. Równolegle działa mechanizm normalnej rozszerzalności omówiony powyżej, którego efekt jest tłumiony przez zmiany struktury wody. Początkowo zagęszczanie struktury dominuje nad normalnym mechanizmem rozszerzalności cieplnej i dlatego mamy zgęszczanie wody. Dopiero począwszy od temperatury czterech stopni Celsjusza mechanizm normalnej rozszerzalności zdobywa przewagę i dla wyższej temperatury woda zachowuje się już normalnie.

Pytania i problemy

1. Zdefiniuj współczynnik rozszerzalności objętościowej. Podaj wartość tego współczynnika dla gazu doskonałego, przy stałym ciśnieniu.
2. Opisz zależność objętości gazu doskonałego od temperatury. Czy zależność ta odnosi się tylko do jednego stanu skupienia materii?
3. Podaj wzór na wzrost wymiarów liniowych ciała pod wpływem wzrostu temperatury. Udowodnij, że wartość współczynnika rozszerzalności objętościowej jest około trzy razy większa od wartości współczynnika rozszerzalności liniowej ciała.
4. Jakie są przyczyny mikroskopowe rozszerzalności termicznej ciał?
5. Na czym polega anomalna rozszerzalność cieplna wody? Wyjaśnij, dlaczego woda zachowuje się inaczej niż typowe ciecze.