1.8. Ruch jednostajnie opóźniony

Jeżeli przyspieszenie $\vec{a}$ jest zwrócone w stronę przeciwną do prędkości $\vec{v}$ ruchu ciała, to wartość prędkości będzie coraz mniejsza i będziemy mieli do czynienia z ruchem opóźnionym. Przyspieszenie zwrócone przeciwnie do prędkości ciała nazywa się opóźnieniem. Jeżeli opóźnienie jest stałe, to ruch nazywamy jednostajnie opóźnionym.

Trzymając się ściśle wzoru (1.11) – definicji przyspieszenia – w postaci:

a=\frac{\Delta v}{\Delta t}=\frac{v-v_{0}}{\Delta t}

( 1.28 )

trzeba przyjąć, że przyspieszenie jest ujemne w ruchu opóźnionym (gdy prędkość ciała jest dodatnia i jej wartość zmniejsza się, bo wtedy $v_{0}>v$ ). Jednakże mówienie o „przyspieszeniu” w ruchu opóźnionym jest niezręczne, dlatego stosuje się termin „opóźnienie” zamiast „wartość bezwzględna ujemnego przyspieszenia”. Opóźnieniu przypisujemy dodatnią wartość, będącą właśnie wartością bezwzględną owego „ujemnego przyspieszenia”.

Wyobraźmy sobie, na przykład, hamujący samochód. Jego prędkość zmniejsza się od $v_{0}$ w chwili $t=0$ do $v$ mniejszego od $v_{0}$ . Zmiana prędkości $\Delta v=v-v_{0}$ jest ujemna, a więc i przyspieszenie $a=\Delta v/\Delta t$ jest ujemne. Zatem opóźnienie jako wartość bezwzględna przyspieszenia ujemnego jest równe ubytkowi prędkości w jednostce czasu:

opóźnienie=a=\left|\frac{\Delta v}{\Delta t}\right|=\left|\frac{v-v_{0}}{\Delta t}\right|=\frac{v-v_{0}}{\Delta t}

Wzory na prędkość (1.15) i położenie (1.18) w ruchu jednostajnie przyspieszonym przechodzą we wzory dla ruchu jednostajnie opóźnionego, gdy zmienimy znak przy $a$ na ujemny. Musimy przy tym pamiętać, że symbolem $a$ oznaczamy w nich opóźnienie.Wtedy wzór na prędkość przyjmie postać:

v=v_{0}-at

( 1.29 )

Prędkość po czasie $t$ jest równa prędkości początkowej $v_{0}$ pomniejszonej o zmianę prędkości $a t$ , jaka się dokonała w czasie $t$ . Wzór (1.29) przedstawia zależność liniową malejącej prędkości od czasu $t$ . Jej wykres jest linią prostą opadająca ku dołowi (il. ). Punkt przecięcia tej prostej z osią czasu wyznacza chwilę $t_{k}$ , w której prędkość zmaleje do zera; $t_{k}$ można otrzymać z równania (1.29), podstawiając $v=0$ . Otrzymamy $0=v_{0}-at$ , skąd:

t_{k}=\frac{v_{0}}{a}

( 1.30 )

W przypadku gdy opóźnienie ciała wywołane jest przez opory ruchu, np. przez tarcie albo hamowanie samochodu, to $t_{k}$ jest czasem trwania ruchu jednostajnie opóźnionego – ciało kończy swój ruch.

W przypadku gdy przyspieszenie zwrócone przeciwnie do prędkości nie przestaje działać, to ciało kontynuuje swój ruchu nawet po osiągnięciu zerowej prędkości. Zmienia się jednak zwrot prędkości ciała. Z taką sytuacją mamy do czynienia np. w przypadku rzutu pionowego do góry (który zostanie omówiony w dalszej części tego rozdziału). W takiej sytuacji następuje zmiana zwrotu prędkości w najwyższym punkcie toru. Na wykresie zależności prędkości od czasu (il. ) dalsze trwanie ruchu obrazuje odcinek linii pod osią czasu.

Ilustracja 1.24. **Wykres zależności prędkości od czasu w ruchu jednostajnie opóźnionym**

Równanie (1.29) obejmuje zarówno ruch „do przodu”, czyli o zwrocie prędkości zgodnym ze zwrotem osi współrzędnej położenia ciała, jak i ze zwrotem przeciwnym (kiedy ciało się cofa); wtedy na wykresie $v$ ma formalnie znak minus, co nie oznacza, oczywiście, że wartość wektora prędkości jest ujemna!

A oto równanie zależności położenia ciała od czasu w ruchu prostoliniowym jednostajnie opóźnionym:

s=s_{0}+v_{0}t-\frac{at^{2}}{2}

( 1.31 )

Wykresem zależności położenia ciała od czasu w ruchu jednostajnie opóźnionym, zgodnie ze wzorem (1.31), jest parabola o gałęziach opadających ku dołowi (il. 1.25). Z wykresu możemy odczytać, że wartość współrzędnej położenia ciała $s$ początkowo się zwiększa, ale coraz wolniej, aż do wartości maksymalnej.

Osiąga maksimum w czasie $t_{k}$ . Dalsza część krzywej oznaczona jest linią przerywaną, dla której wartość współrzędnej położenia ciała maleje. Oznacza to, że w tym czasie ciało się cofa.

Ilustracja 1.25. **Wykres zależności położenia $s$ od czasu $t$ w ruchu jednostajnie opóźnionym**

Przykład 6

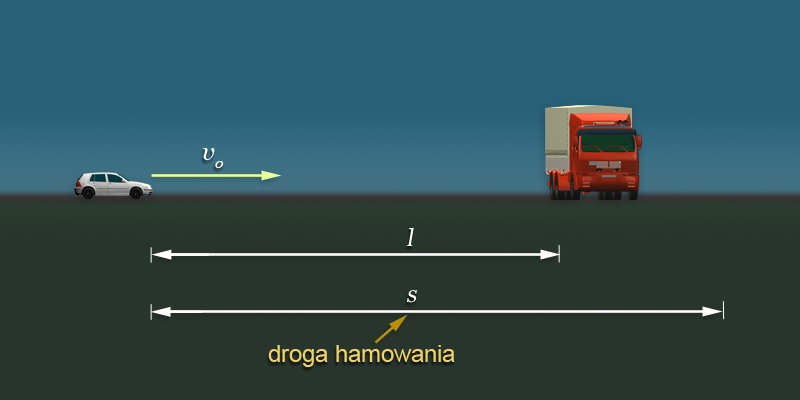
Samochód jedzie z prędkością $v_{0}=100\, km/h$ . Nagle kierowca zauważa przeszkodę w odległości $l=50\, m$ . Czy ma on możliwość uniknięcia zderzenia z przeszkodą, jeżeli największe dostępne opóźnienie podczas hamowania wynosi $a=4,9\, m/s^{2}$ ?

Ilustracja 1.27. **Samochód hamujący przed przeszkodą**

Rozwiązanie: Zakładamy, że podczas hamowania ruch samochodu jest jednostajnie opóźniony. Obliczymy drogę, jaką przebyłby samochód, gdyby nie napotkał przeszkody. Przyjmijmy, że

s_{0}=0

, zatem wzór (1.31) przyjmie postać:

s=v_{0}t-\frac{at^{2}}{2}

Po podstawieniu do niego czasu hamowania wyrażonego wzorem (1.30):

t=t_{k}=\frac{v_{0}}{a}

, otrzymamy:

s=v_{0}\left(\frac{v_{0}}{a}\right)-\frac{a}{2}\left(\frac{v_{0}}{a}\right)^{2}=\frac{v_{0}^{2}}{2a}

Prędkość początkowa samochodu wyrażona w metrach na sekundę wynosi:

v_{0}=100\,\frac{km}{h}=\frac{100\,000\, m}{3\,600\, s}=27,78\frac{m}{s}

Zatem:

s=\frac{\left(27,78\,\frac{m}{s}\right)^{2}}{2\cdot4,9\,\frac{m}{s^{2}}}=78,7\, m

Widzimy, że droga hamowania $s$ jest znacznie większa od odległości $l=50\, m$ od przeszkody! Kierowca nie jest w stanie uniknąć zderzenia.

Obliczmy jeszcze prędkość $v$ , z jaką samochód uderzy w przeszkodę. Znamy drogę $l$ oraz prędkość początkową $v_{0}$ , ale nie znamy czasu $t$ dotarcia samochodu do przeszkody. Zgodnie z równaniem (1.29) czas ten jest równy:

t=\frac{v_{0}-v}{a}

Tak wyrażony czas podstawiamy do wzoru (1.22):

l=v_{0}t=\frac{at^{2}}{2}=v_{0}\frac{v_{0}-v}{a}-\frac{a}{2}\cdot\frac{\left(v_{0}-v\right)^{2}}{a^{2}}

Stąd

l=\frac{v_{0}^{2}-v^{2}}{2a}

Rozwiązując to równanie względem $v$ , otrzymamy szukaną prędkość zderzenia samochodu z przeszkodą:

v=\sqrt{v_{0}^{2}-2al}=\sqrt{\left(27,78\,\frac{m}{s}\right)^{2}-2\cdot4,9\,\frac{m}{s^{2}}\cdot50\, m}=16,78\,\frac{m}{s}=60,4\,\frac{km}{h}

Samochód uderzy więc w przeszkodę z prędkością o wartości 60,4 km/h.

Przykład 7

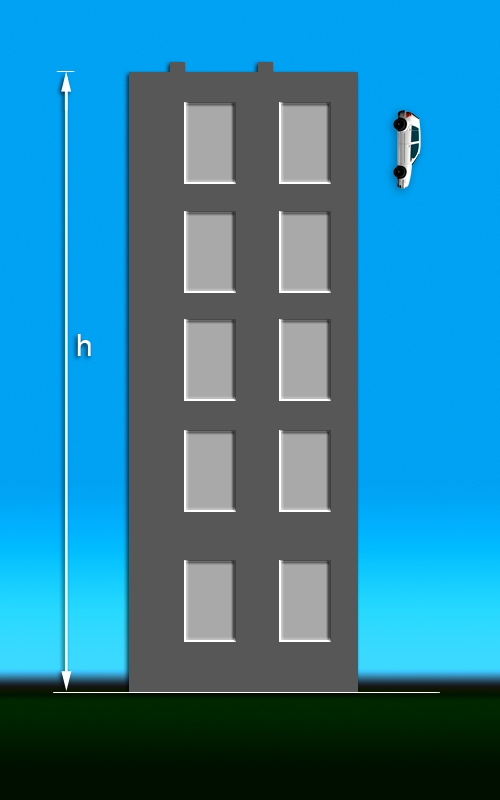
Wyobraź sobie, że samochód spada z pewnej wysokości $h$ i uzyskuje prędkość taką, jak obliczona w przykładzie Przykład 6 (60,4 km/h). Oblicz tę wysokość.

Rozwiązanie: Samochód podczas swego hipotetycznego upadku porusza się ruchem jednostajnie przyspieszonym, z początkową prędkością $v_{0}=0$ , z przyspieszeniem ziemskim $g$ , przebywając w czasie $t$ drogę równą $h$ . Wykorzystajmy więc wzór $h=\frac{gt^{2}}{2}$ oraz wzór $v=gt$ w następujący sposób:

h=\frac{gt^{2}}{2}=\frac{g^{2}t^{2}}{2g}=\frac{\left(gt\right)^{2}}{2g}=\frac{v^{2}}{2g}

Ilustracja 1.28. **Spadający samochód**

Efekt zderzenia z przeszkodą samochodu jadącego z prędkością 60 km/h odpowiada upadkowi samochodu z dachu budynku czteropiętrowego

Zatem:

h=\frac{v^{2}}{2g}=\frac{\left(16,78\, m/s\right)^{2}}{2\cdot9,81\, m/s^{2}}=14,35\, m

Jest to (w przybliżeniu) wysokość budynku czteropiętrowego. Innymi słowy, samochód zderzy się z przeszkodą z prędkością, jaką uzyskałby przy upadku z dachu czteropiętrowego budynku (il. 1.28).

Pytania i problemy

Wytłumacz, czym różni się ruch jednostajnie przyspieszony od ruchu jednostajnie opóźnionego.
Wyjaśnij, co to jest opóźnienie. Dlaczego stosujemy określenie „opóźnienie”, a nie „ujemne przyspieszenie”?
Opisz podobieństwa i różnice między wzorami na położenie i prędkość w ruchu jednostajnie przyspieszonym a ich odpowiednikami w ruchu jednostajnie opóźnionym.
Wykonaj wykres zależności położenia $s$ od czasu $t$ w ruchach jednostajnie zmiennych wg przykładów: Przykład 6 i Przykład 7.
Wykonaj wykres zależności prędkości od czasu w ruchach jednostajnie zmiennych wg przykładów: Przykład 6 i Przykład 7.